Physics

't Hooft, Gerard and Stefan Vandoren. Time in Powers of Ten. Singapore: World Scientific, 2014. ISBN 978-981-4489-81-2.

Phenomena in the universe take place over scales ranging from the unimaginably small to the breathtakingly large. The classic film, Powers of Ten, produced by Charles and Ray Eames, and the companion book explore the universe at length scales in powers of ten: from subatomic particles to the most distant visible galaxies. If we take the smallest meaningful distance to be the Planck length, around 10⁻³⁵ metres, and the diameter of the observable universe as around 10²⁷ metres, then the ratio of the largest to smallest distances which make sense to speak of is around 10⁶². Another way to express this is to answer the question, “How big is the universe in Planck lengths?” as “Mega, mega, yotta, yotta big!”

But length isn't the only way to express the scale of the universe. In the present book, the authors examine the time intervals at which phenomena occur or recur. Starting with one second, they take steps of powers of ten (10, 100, 1000, 10000, etc.), arriving eventually at the distant future of the universe, after all the stars have burned out and even black holes begin to disappear. Then, in the second part of the volume, they begin at the Planck time, 5×10⁻⁴⁴ seconds, the shortest unit of time about which we can speak with our present understanding of physics, and again progress by powers of ten until arriving back at an interval of one second.

Intervals of time can denote a variety of different phenomena, which are colour coded in the text. A period of time can mean an epoch in the history of the universe, measured from an event such as the Big Bang or the present; a distance defined by how far light travels in that interval; a recurring event, such as the orbital period of a planet or the frequency of light or sound; or the half-life of a randomly occurring event such as the decay of a subatomic particle or atomic nucleus.

Because the universe is still in its youth, the range of time intervals discussed here is much larger than those when considering length scales. From the Planck time of 5×10⁻⁴⁴ seconds to the lifetime of the kind of black hole produced by a supernova explosion, 10⁷⁴ seconds, the range of intervals discussed spans 118 orders of magnitude. If we include the evaporation through Hawking radiation of the massive black holes at the centres of galaxies, the range is expanded to 143 orders of magnitude. Obviously, discussions of the distant future of the universe are highly speculative, since in those vast depths of time physical processes which we have never observed due to their extreme rarity may dominate the evolution of the universe.

Among the fascinating facts you'll discover is that many straightforward physical processes take place over an enormous range of time intervals. Consider radioactive decay. It is possible, using a particle accelerator, to assemble a nucleus of hydrogen-7, an isotope of hydrogen with a single proton and six neutrons. But if you make one, don't grow too fond of it, because it will decay into tritium and four neutrons with a half-life of 23×10⁻²⁴ seconds, an interval usually associated with events involving unstable subatomic particles. At the other extreme, a nucleus of tellurium-128 decays into xenon with a half-life of 7×10³¹ seconds (2.2×10²⁴ years), more than 160 trillion times the present age of the universe.

While the very short and very long are the domain of physics, intermediate time scales are rich with events in geology, biology, and human history. These are explored, along with how we have come to know their chronology. You can open the book to almost any page and come across a fascinating story. Have you ever heard of the ocean quahog (Arctica islandica)? They're clams, and the oldest known has been determined to be 507 years old, born around 1499 and dredged up off the coast of Iceland in 2006. People eat them.

Or did you know that if you perform carbon-14 dating on grass growing next to a highway, the lab will report that it's tens of thousands of years old? Why? Because the grass has incorporated carbon from the CO₂ produced by burning fossil fuels which are millions of years old and contain little or no carbon-14.

This is a fascinating read, and one which uses the framework of time intervals to acquaint you with a wide variety of sciences, each inviting further exploration. The writing is accessible to the general reader, young adult and older. The individual entries are short and stand alone—if you don't understand something or aren't interested in a topic, just skip to the next. There are abundant colour illustrations and diagrams.

Author Gerard 't Hooft won the 1999 Nobel Prize in Physics for his work on the quantum mechanics of the electroweak interaction. The book was originally published in Dutch in the Netherlands in 2011. The English translation was done by 't Hooft's daughter, Saskia Eisberg-'t Hooft. The translation is fine, but there are a few turns of phrase which will seem odd to an English mother tongue reader. For example, matter in the early universe is said to “clot” under the influence of gravity; the common English term for this is “clump”. This is a translation, not a re-write: there are a number of references to people, places, and historical events which will be familiar to Dutch readers but less so to those in the Anglosphere. In the Kindle edition notes, cross-references, the table of contents, and the index are all properly linked, and the illustrations are reproduced well.

October 2016 

Adams, Fred and Greg Laughlin. The Five Ages of the Universe. New York: The Free Press, 1999. ISBN 0-684-85422-8.

April 2001 

Barrow, John D. The Constants of Nature. New York: Pantheon Books, 2002. ISBN 0-375-42221-8.

This main body copy in this book is set in a type font in which the digit “1” is almost indistinguishable from the capital letter “I”. Almost—look closely at the top serif on the “1” and you'll note that it rises toward the right while the “I” has a horizontal top serif. This struck my eye as ugly and antiquated, but I figured I'd quickly get used to it. Nope: it looked just as awful on the last page as in the first chapter. Oddly, the numbers on pages 73 and 74 use a proper digit “1”, as do numbers within block quotations.

June 2003 

Barrow, John D. The Infinite Book. New York: Vintage Books, 2005. ISBN 1-4000-3224-5.

Don't panic—despite the title, this book is only 330 pages! Having written an entire book about nothing (The Book of Nothing, May 2001), I suppose it's only natural the author would take on the other end of the scale. Unlike Rudy Rucker's Infinity and the Mind, long the standard popular work on the topic, Barrow spends only about half of the book on the mathematics of infinity. Philosophical, metaphysical, and theological views of the infinite in a variety of cultures are discussed, as well as the history of the infinite in mathematics, including a biographical portrait of the ultimately tragic life of Georg Cantor. The physics of an infinite universe (and whether we can ever determine if our own universe is infinite), the paradoxes of an infinite number of identical copies of ourselves necessarily existing in an infinite universe, the possibility of machines which perform an infinite number of tasks in finite time, whether we're living in a simulation (and how we might discover we are), and the practical and moral consequences of immortality and time travel are also explored.

Mathematicians and scientists have traditionally been very wary of the infinite (indeed, the appearance of infinities is considered an indication of the limitations of theories in modern physics), and Barrow presents any number of paradoxes which illustrate that, as he titles chapter four, “infinity is not a big number”: it is fundamentally different and requires a distinct kind of intuition if nonsensical results are to be avoided. One of the most delightful examples is Zhihong Xia's five-body configuration of point masses which, under Newtonian gravitation, expands to infinite size in finite time. (Don't worry: the finite speed of light, formation of an horizon if two bodies approach too closely, and the emission of gravitational radiation keep this from working in the relativistic universe we inhabit. As the author says [p. 236], “Black holes might seem bad but, like growing old, they are really not so bad when you consider the alternatives.”)

This is an enjoyable and enlightening read, but I found it didn't come up to the standard set by The Book of Nothing and The Constants of Nature (June 2003). Like the latter book, this one is set in a hideously inappropriate font for a work on mathematics: the digit “1” is almost indistinguishable from the letter “I”. If you look very closely at the top serif on the “1” you'll note that it rises toward the right while the “I” has a horizontal top serif. But why go to the trouble of distinguishing the two characters and then making the two glyphs so nearly identical you can't tell them apart without a magnifying glass? In addition, the horizontal bar of the plus sign doesn't line up with the minus sign, which makes equations look awful.

This isn't the author's only work on infinity; he's also written a stage play, Infinities, which was performed in Milan in 2002 and 2003.

September 2007 

Barrow, John D., Paul C.W. Davies, and Charles L. Harper, Jr., eds. Science and Ultimate Reality. Cambridge: Cambridge University Press, 2004. ISBN 0-521-83113-X.

These are the proceedings of the festschrift at Princeton in March 2002 in honour of John Archibald Wheeler's 90th year within our light-cone. This volume brings together the all-stars of speculative physics, addressing what Wheeler describes as the “big questions.” You will spend a lot of time working your way through this almost 700 page tome (which is why entries in this reading list will be uncharacteristically sparse this month), but it will be well worth the effort. Here we have Freeman Dyson posing thought-experiments which purport to show limits to the applicability of quantum theory and the uncertainty principle, then we have Max Tegmark on parallel universes, arguing that the most conservative model of cosmology has infinite copies of yourself within the multiverse, each choosing either to read on here or click another link. Hideo Mabuchi's chapter begins with an introductory section which is lyrical prose poetry up to the standard set by Wheeler, and if Shou-Cheng Zhang's final chapter doesn't make you re-think where the bottom of reality really lies, you're either didn't get it or have been spending way too much time reading preprints on ArXiv. I don't mean to disparage any of the other contributors by not mentioning them—every chapter of this book is worth reading, then re-reading carefully. This is the collected works of the 21th century equivalent of the savants who attended the Solvay Congresses in the early 20th century. Take your time, reread difficult material as necessary, and look up the references. You'll close this book in awe of what we've learned in the last 20 years, and in wonder of what we'll discover and accomplish the the rest of this century and beyond.

July 2004 

Behe, Michael J., William A. Dembski, and Stephen C. Meyer. Science and Evidence for Design in the Universe. San Francisco: Ignatius Press, 2000. ISBN 0-89870-809-5.

March 2002 

Bell, John S. Speakable and Unspeakable in Quantum Mechanics. Cambridge: Cambridge University Press, [1987] 1993. ISBN 0-521-52338-9.

This volume collects most of Bell's papers on the foundations and interpretation of quantum mechanics including, of course, his discovery of “Bell's inequality”, which showed that no local hidden variable theory can reproduce the statistical results of quantum mechanics, setting the stage for the experimental confirmation by Aspect and others of the fundamental non-locality of quantum physics. Bell's interest in the pilot wave theories of de Broglie and Bohm is reflected in a number of papers, and Bell's exposition of these theories is clearer and more concise than anything I've read by Bohm or Hiley. He goes on to show the strong similarities between the pilot wave approach and the “many world interpretation” of Everett and de Witt. An extra added treat is chapter 9, where Bell derives special relativity entirely from Maxwell's equations and the Bohr atom, along the lines of Fitzgerald, Larmor, Lorentz, and Poincaré, arriving at the principle of relativity (which Einstein took as a hypothesis) from the previously known laws of physics.

October 2004 

Benford, Gregory ed. Far Futures. New York: Tor, 1995. ISBN 0-312-86379-9.

July 2003 

Bernstein, Jeremy. Plutonium. Washington: Joseph Henry Press, 2007. ISBN 0-309-10296-0.

When the Manhattan Project undertook to produce a nuclear bomb using plutonium-239, the world's inventory of the isotope was on the order of a microgram, all produced by bombarding uranium with neutrons produced in cyclotrons. It wasn't until August of 1943 that enough had been produced to be visible under a microscope. When, in that month, the go-ahead was given to build the massive production reactors and separation plants at the Hanford site on the Columbia River, virtually nothing was known of the physical properties, chemistry, and metallurgy of the substance they were undertaking to produce. In fact, it was only in 1944 that it was realised that the elements starting with thorium formed a second group of “rare earth” elements: the periodic table before World War II had uranium in the column below tungsten and predicted that the chemistry of element 94 would resemble that of osmium. When the large-scale industrial production of plutonium was undertaken, neither the difficulty of separating the element from the natural uranium matrix in which it was produced nor the contamination with Pu-240 which would necessitate an implosion design for the plutonium bomb were known. Notwithstanding, by the end of 1947 a total of 500 kilograms of the stuff had been produced, and today there are almost 2000 metric tons of it, counting both military inventories and that produced in civil power reactors, which crank out about 70 more metric tons a year.

These are among the fascinating details gleaned and presented in this history and portrait of the most notorious of artificial elements by physicist and writer Jeremy Bernstein. He avoids getting embroiled in the building of the bomb, which has been well-told by others, and concentrates on how scientists around the world stumbled onto nuclear fission and transuranic elements, puzzled out what they were seeing, and figured out the bizarre properties of what they had made. Bizarre is not too strong a word for the chemistry and metallurgy of plutonium, which remains an active area of research today with much still unknown. When you get that far down on the periodic table, both quantum mechanics and special relativity get into the act (as they start to do even with gold), and you end up with six allotropic phases of the metal (in two of which volume decreases with increasing temperature), a melting point of just 640° C and an anomalous atomic radius which indicates its 5f electrons are neither localised nor itinerant, but somewhere in between.

As the story unfolds, we meet some fascinating characters, including Fritz Houtermans, whose biography is such that, as the author notes (p. 86), “if one put it in a novel, no one would find it plausible.” We also meet stalwarts of the elite 26-member UPPU Club: wartime workers at Los Alamos whose exposure to plutonium was sufficient that it continues to be detectable in their urine. (An epidemiological study of these people which continues to this day has found no elevated rates of mortality, which is not to say that plutonium is not a hideously hazardous substance.)

The text is thoroughly documented in the end notes, and there is an excellent index; the entire book is just 194 pages. I have two quibbles. On p. 110, the author states of the Little Boy gun-assembly uranium bomb dropped on Hiroshima, “This is the only weapon of this design that was ever detonated.” Well, I suppose you could argue that it was the only such weapon of that precise design detonated, but the implication is that it was the first and last gun-type bomb to be detonated, and this is not the case. The U.S. W9 and W33 weapons, among others, were gun-assembly uranium bombs, which between them were tested three times at the Nevada Test Site. The price for plutonium-239 quoted on p. 155, US$5.24 per milligram, seems to imply that the plutonium for a critical mass of about 6 kg costs about 31 million dollars. But this is because the price quoted is for 99–99.99% isotopically pure Pu-239, which has been electromagnetically separated from the isotopic mix you get from the production reactor. Weapons-grade plutonium can have up to 7% Pu-240 contamination, which doesn't require the fantastically expensive isotope separation phase, just chemical extraction of plutonium from reactor fuel. In fact, you can build a bomb from so-called “reactor-grade” plutonium—the U.S. tested one in 1962.

November 2007 

Bethell, Tom. Questioning Einstein. Pueblo West, CO: Vales Lake Publishing, 2009. ISBN 978-0-9714845-9-7.

Call it my guilty little secret. Every now and then, I enjoy nothing more than picking up a work of crackpot science, reading it with the irony lobe engaged, and figuring out precisely where the author went off the rails and trying to imagine how one might explain to them the blunders which led to the poppycock they expended so much effort getting into print. In the field of physics, for some reason Einstein's theory of special relativity attracts a disproportionate number of such authors, all bent on showing that Einstein was wrong or, in the case of the present work's subtitle, asking “Is Relativity Necessary?”. With a little reflexion, this shouldn't be a surprise: alone among major theories of twentieth century physics, special relativity is mathematically accessible to anybody acquainted with high school algebra, and yet makes predictions for the behaviour of objects at high velocity which are so counterintuitive to the expectations based upon our own personal experience with velocities much smaller than that they appear, at first glance, to be paradoxes. Theories more dubious and less supported by experiment may be shielded from crackpots simply by the forbidding mathematics one must master in order to understand and talk about them persuasively.

This is an atypical exemplar of the genre. While most attacks on special relativity are written by delusional mad scientists, the author of the present work, Tom Bethell, is a respected journalist whose work has been praised by, among others, Tom Wolfe and George Gilder. The theory presented here is not his own, but one developed by Petr Beckmann, whose life's work, particularly in advocating civil nuclear power, won him the respect of Edward Teller (who did not, however, endorse his alternative to relativity). As works of crackpot science go, this is one of the best I've read. It is well written, almost free of typographical and factual errors, clearly presents its arguments in terms a layman can grasp, almost entirely avoids mathematical equations, and is thoroughly documented with citations of original sources, many of which those who have learnt special relativity from modern textbooks may not be aware. Its arguments against special relativity are up to date, tackling objections including the Global Positioning System, the Brillet-Hall experiment, and the Hafele-Keating “travelling clock” experiments as well as the classic tests. And the author eschews the ad hominem attacks on Einstein which are so common in the literature of opponents to relativity.

Beckmann's theory posits that the luminiferous æther (the medium in which light waves propagate), which was deemed “superfluous” in Einstein's 1905 paper, in fact exists, and is simply the locally dominant gravitational field. In other words, the medium in which light waves wave is the gravity which makes things which aren't light heavy. Got it? Light waves in any experiment performed on the Earth or in its vicinity will propagate in the æther of its gravitational field (with only minor contributions from those of other bodies such as the Moon and Sun), and hence attempts to detect the “æther drift” due to the Earth's orbital motion around the Sun such as the Michelson-Morley experiment will yield a null result, since the æther is effectively “dragged” or “entrained” along with the Earth. But since the gravitational field is generated by the Earth's mass, and hence doesn't rotate with it (Huh—what about the Lense-Thirring effect, which is never mentioned here?), it should be possible to detect the much smaller æther drift effect as the measurement apparatus rotates around the Earth, and it is claimed that several experiments have made such a detection.

It's traditional that popular works on special relativity couch their examples in terms of observers on trains, so let me say that it's here that we feel the sickening non-inertial-frame lurch as the train departs the track and enters a new inertial frame headed for the bottom of the canyon. Immediately, we're launched into a discussion of the Sagnac effect and its various manifestations ranging from the original experiment to practical applications in laser ring gyroscopes, to round-the-world measurements bouncing signals off multiple satellites. For some reason the Sagnac effect seems to be a powerful attractor into which special relativity crackpottery is sucked. Why it is so difficult to comprehend, even by otherwise intelligent people, entirely escapes me. May I explain it to you? This would be easier with a diagram, but just to show off and emphasise how simple it is, I'll do it with words. Imagine you have a turntable, on which are mounted four mirrors which reflect light around the turntable in a square: the light just goes around and around. If the turntable is stationary and you send a pulse of light in one direction around the loop and then send another in the opposite direction, it will take precisely the same amount of time for them to complete one circuit of the mirrors. (In practice, one uses continuous beams of monochromatic light and combines them in an interferometer, but the effect is the same as measuring the propagation time—it's just easier to do it that way.) Now, let's assume you start the turntable rotating clockwise. Once again you send pulses of light around the loop in both directions; this time we'll call the one which goes in the same direction as the turntable's rotation the clockwise pulse and the other the counterclockwise pulse. Now when we measure how long it took for the clockwise pulse to make it one time around the loop we find that it took longer than for the counterclockwise pulse. OMG!!! Have we disproved Einstein's postulate of the constancy of the speed of light (as is argued in this book at interminable length)? Well, of course not, as a moment's reflexion will reveal. The clockwise pulse took longer to make it around the loop because it had farther to travel to arrive there: as it was bouncing from each mirror to the next, the rotation of the turntable was moving the next mirror further away, and so each leg it had to travel was longer. Conversely, as the counterclockwise pulse was in flight, its next mirror was approaching it, and hence by the time it made it around the loop it had travelled less far, and consequently arrived sooner. That's all there is to it, and precision measurements of the Sagnac effect confirm that this analysis is completely consistent with special relativity. The only possible source of confusion is if you make the self-evident blunder of analysing the system in the rotating reference frame of the turntable. Such a reference frame is trivially non-inertial, so special relativity does not apply. You can determine this simply by tossing a ball from one side of the turntable to another, with no need for all the fancy mirrors, light pulses, or the rest.

Other claims of Beckmann's theory are explored, all either dubious or trivially falsified. Bethell says there is no evidence for the length contraction predicted by special relativity. In fact, analysis of heavy ion collisions confirm that each nucleus approaching the scene of the accident “sees” the other as a “pancake” due to relativistic length contraction. It is claimed that while physical processes on a particle moving rapidly through a gravitational field slow down, that an observer co-moving with that particle would not see a comparable slow-down of clocks at rest with respect to that gravitational field. But the corrections applied to the atomic clocks in GPS satellites incorporate this effect, and would produce incorrect results if it did not occur.

I could go on and on. I'm sure there is a simple example from gravitational lensing or propagation of electromagnetic radiation from gamma ray bursts which would falsify the supposed classical explanation for the gravitational deflection of light due to a refractive effect based upon strength of the gravitational field, but why bother when so many things much easier to dispose of are hanging lower on the tree. Should you buy this book? No, unless, like me, you enjoy a rare example of crackpot science which is well done. This is one of those, and if you're well acquainted with special relativity (if not, take a trip on our C-ship!) you may find it entertaining finding the flaws in and identifying experiments which falsify the arguments here.

January 2011 

Bjornson, Adrian. A Universe that We Can Believe. Woburn, Massachusetts: Addison Press, 2000. ISBN 0-9703231-0-7.

December 2001 

Bockris, John O'M. The New Paradigm. College Station, TX: D&M Enterprises, 2005. ISBN 0-9767444-0-6.

As the nineteenth century gave way to the twentieth, the triumphs of classical science were everywhere apparent: Newton's theories of mechanics and gravitation, Maxwell's electrodynamics, the atomic theory of chemistry, Darwin's evolution, Mendel's genetics, and the prospect of formalising all of mathematics from a small set of logical axioms. Certainly, there were a few little details awaiting explanation: the curious failure to detect ether drift in the Michelson-Morley experiment, the pesky anomalous precession of the perihelion of the planet Mercury, the seeming contradiction between the equipartition of energy and the actual spectrum of black body radiation, the mysterious patterns in the spectral lines of elements, and the source of the Sun's energy, but these seemed matters the next generation of scientists could resolve by building on the firm foundation laid by the last. Few would have imagined that these curiosities would spark a thirty year revolution in physics which would show the former foundations of science to be valid only in the limits of slow velocities, weak fields, and macroscopic objects.

At the start of the twenty-first century, in the very centennial of Einstein's annus mirabilis, it is only natural to enquire how firm are the foundations of present-day science, and survey the “little details and anomalies” which might point toward scientific revolutions in this century. That is the ambitious goal of this book, whose author's long career in physical chemistry began in 1945 with a Ph.D. from Imperial College, London, and spanned more than forty years as a full professor at the University of Pennsylvania, Flinders University in Australia, and Texas A&M University, where he was Distinguished Professor of Energy and Environmental Chemistry, with more than 700 papers and twenty books to his credit. And it is at this goal that Professor Bockris utterly, unconditionally, and irredeemably fails. By the evidence of the present volume, the author, notwithstanding his distinguished credentials and long career, is a complete idiot.

That's not to say you won't learn some things by reading this book. For example, what do physicists Hendrik Lorentz, Werner Heisenberg, Hannes Alfvén, Albert A. Michelson, and Lord Rayleigh; chemist Amedeo Avogadro, astronomers Chandra Wickramasinghe, Benik Markarian, and Martin Rees; the Weyerhaeuser Company; the Doberman Pinscher dog breed; Renaissance artist Michelangelo; Cepheid variable stars; Nazi propagandist Joseph Goebbels; the Menninger Foundation and the Cavendish Laboratory; evolutionary biologist Richard Dawkins; religious figures Saint Ignatius of Antioch, Bishop Berkeley, and Teilhard de Chardin; parapsychologists York Dobyns and Brenda Dunne; anomalist William R. Corliss; and Centreville Maryland, Manila in the Philippines, and the Galapagos Islands all have in common?

(Show answer)

(Hide answer)
Their names are all misspelled in this book. Werner Heisenberg shares the distinction of having his name spelt three different ways, providing a fine example of Heisenberg uncertainty, although Chandra Wickramasinghe takes the prize with three different incorrect spellings within five pages: “Wickrisingam” (p. 146), “Wackrisingham” (p. 147), and “Wackrasingham” (p. 150). Even Bockris could not wackily rise to the challenge of misspelling the last names of statistician I. J. Good or physicist T. D. Lee—so he got their initials wrong! Evidently, the author's memory for names is phonetic, not visual, and none too accurate; when a citation is required, he just hits whatever keys resemble his recollection of the name, and never bothers to get up and check the correct attribution on his bookshelf.

The “Shaking Pillars of the Paradigm” about which the author expresses sentiments ranging from doubt to disdain in chapter 3 include mathematics (where he considers irrational roots, non-commutative multiplication of quaternions, and the theory of limits among flaws indicative of the “break down” of mathematical foundations [p. 71]), Darwinian evolution, special relativity, what he refers to as “The So-Called General Theory of Relativity” with only the vaguest notion of its content—yet is certain is dead wrong, quantum theory (see p. 120 for a totally bungled explanation of Schrodinger's cat in which he seems to think the result depends upon a decision made by the cat), the big bang (which he deems “preposterus” on p. 138) and the Doppler interpretation of redshifts, and naturalistic theories of the origin of life. Chapter 4 begins with the claim that “There is no physical model which can tell us why [electrostatic] attraction and repulsion occur” (p. 163).

And what are those stubborn facts in which the author does believe, or at least argues merit the attention of science, pointing the way to a new foundation for science in this century? Well, that would be: UFOs and alien landings; Kirlian photography; homeopathy and Jacques Benveniste's “imprinting of water”; crop circles; Qi Gong masters remotely changing the half-life of radioactive substances; the Maharishi Effect and “Vedic Physics”; “cold fusion” and the transmutation of base metals into gold (on both of which the author published while at Texas A&M); telepathy, clairvoyance, and precognition; apparitions, poltergeists, haunting, demonic possession, channelling, and appearances of the Blessed Virgin Mary; out of body and near-death experiences; survival after death, communication through mediums including physical manifestations, and reincarnation; and psychokinesis, faith and “anomalous” healing (including the “psychic surgeons” of the Philippines), and astrology. The only apparent criterion for the author's endorsement of a phenomenon appears to be its rejection by mainstream science.

Now, many works of crank science can be quite funny, and entirely worth reading for their amusement value. Sadly, this book is so poorly written it cannot be enjoyed even on that level. In the introduction to this reading list I mention that I don't include books which I didn't finish, but that since I've been keeping the list I've never abandoned a book partway through. Well, my record remains intact, but this one sorely tempted me. The style, if you can call it that, is such that one finds it difficult to believe English is the author's mother tongue, no less that his doctorate is from a British university at a time when language skills were valued. The prose is often almost physically painful to read. Here is an example, from footnote 37 on page 117—but you can find similar examples on almost any page; I've chosen this one because it is, in addition, almost completely irrelevant to the text it annotates.

Here, it is relevant to describe a corridor meeting with a mature colleague - keen on Quantum Mechanical calculations, - who had not the friends to give him good grades in his grant applications and thus could not employ students to work with him. I commiserated on his situation, - a professor in a science department without grant money. How can you publish I blurted out, rather tactlessly. “Ah, but I have Lili” he said (I've changed his wife's name). I knew Lili, a pleasant European woman interested in obscure religions. She had a high school education but no university training. “But” … I began to expostulate. “It's ok, ok”, said my colleague. “Well, we buy the programs to calculate bond strengths, put it in the computer and I tell Lili the quantities and she writes down the answer the computer gives. Then, we write a paper.” The program referred to is one which solves the Schrödinger equation and provides energy values, e.g., for bond strength in chemical compounds.

Now sit back, close your eyes, and imagine five hundred pages of this; in spelling, grammar, accuracy, logic, and command of the subject matter it reads like a textbook-length Slashdot post. Several recurrent characteristics are manifest in this excerpt. The author repeatedly, though not consistently, capitalises Important Words within Sentences; he uses hyphens where em-dashes are intended, and seems to have invented his own punctuation sign: a comma followed by a hyphen, which is used interchangeably with commas and em-dashes. The punctuation gives the impression that somebody glanced at the manuscript and told the author, “There aren't enough commas in it”, whereupon he went through and added three or four thousand in completely random locations, however inane. There is an inordinate fondness for “e.g.”, “i.e.”, and “cf.”, and they are used in ways which make one suspect the author isn't completely clear on their meaning or the distinctions among them. And regarding the footnote quoted above, did I mention that the author's wife is named “Lily”, and hails from Austria?

Further evidence of the attention to detail and respect for the reader can be found in chapter 3 where most of the source citations in the last thirty pages are incorrect, and the blank cross-references scattered throughout the text. Not only is it obvious the book has not been fact checked, nor even proofread; it has never even been spelling checked—common words are misspelled all over. Bockris never manages the Slashdot hallmark of misspelling “the”, but on page 475 he misspells “to” as “ot”. Throughout you get the sense that what you're reading is not so much a considered scientific exposition and argument, but rather the raw unedited output of a keystroke capturing program running on the author's computer.

Some readers may take me to task for being too harsh in these remarks, noting that the book was self-published by the author at age 82. (How do I know it was self-published? Because my copy came with the order from Amazon to the publisher to ship it to their warehouse folded inside, and the publisher's address in this document is directly linked to the author.) Well, call me unkind, but permit me to observe that readers don't get a quality discount based on the author's age from the price of US$34.95, which is on the very high end for a five hundred page paperback, nor is there a disclaimer on the front or back cover that the author might not be firing on all cylinders. Certainly, an eminent retired professor ought to be able to call on former colleagues and/or students to review a manuscript which is certain to become an important part of his intellectual legacy, especially as it attempts to expound a new paradigm for science. Even the most cursory editing to remove needless and tedious repetition could knock 100 pages off this book (and eliminating the misinformation and nonsense could probably slim it down to about ten). The vast majority of citations are to secondary sources, many popular science or new age books.

Apart from these drawbacks, Bockris, like many cranks, seems compelled to personally attack Einstein, claiming his work was derivative, hinting at plagiarism, arguing that its significance is less than its reputation implies, and relating an unsourced story claiming Einstein was a poor husband and father (and even if he were, what does that have to do with the correctness and importance of his scientific contributions?). In chapter 2, he rants upon environmental and economic issues, calls for a universal dole (p. 34) for those who do not work (while on p. 436 he decries the effects of just such a dole on Australian youth), calls (p. 57) for censorship of music, compulsory population limitation, and government mandated instruction in philosophy and religion along with promotion of religious practice. Unlike many radical environmentalists of the fascist persuasion, he candidly observes (p. 58) that some of these measures “could not achieved under the present conditions of democracy”. So, while repeatedly inveighing against the corruption of government-funded science, he advocates what amounts to totalitarian government—by scientists.

December 2005 

Brown, Brandon R. Planck. Oxford: Oxford University Press, 2015. ISBN 978-0-19-021947-5.

Theoretical physics is usually a young person's game. Many of the greatest breakthroughs have been made by researchers in their twenties, just having mastered existing theories while remaining intellectually flexible and open to new ideas. Max Planck, born in 1858, was an exception to this rule. He spent most of his twenties living with his parents and despairing of finding a paid position in academia. He was thirty-six when he took on the project of understanding heat radiation, and forty-two when he explained it in terms which would launch the quantum revolution in physics. He was in his fifties when he discovered the zero-point energy of the vacuum, and remained engaged and active in science until shortly before his death in 1947 at the age of 89. As theoretical physics editor for the then most prestigious physics journal in the world, Annalen der Physik, in 1905 he approved publication of Einstein's special theory of relativity, embraced the new ideas from a young outsider with neither a Ph.D. nor an academic position, extended the theory in his own work in subsequent years, and was instrumental in persuading Einstein to come to Berlin, where he became a close friend.

Sometimes the simplest puzzles lead to the most profound of insights. At the end of the nineteenth century, the radiation emitted by heated bodies was such a conundrum. All objects emit electromagnetic radiation due to the thermal motion of their molecules. If an object is sufficiently hot, such as the filament of an incandescent lamp or the surface of the Sun, some of the radiation will fall into the visible range and be perceived as light. Cooler objects emit in the infrared or lower frequency bands and can be detected by instruments sensitive to them. The radiation emitted by a hot object has a characteristic spectrum (the distribution of energy by frequency), and has a peak which depends only upon the temperature of the body. One of the simplest cases is that of a black body, an ideal object which perfectly absorbs all incident radiation. Consider an ideal closed oven which loses no heat to the outside. When heated to a given temperature, its walls will absorb and re-emit radiation, with the spectrum depending upon its temperature. But the equipartition theorem, a cornerstone of statistical mechanics, predicted that the absorption and re-emission of radiation in the closed oven would result in a ever-increasing peak frequency and energy, diverging to infinite temperature, the so-called ultraviolet catastrophe. Not only did this violate the law of conservation of energy, it was an affront to common sense: closed ovens do not explode like nuclear bombs. And yet the theory which predicted this behaviour, the Rayleigh-Jeans law, made perfect sense based upon the motion of atoms and molecules, correctly predicted numerous physical phenomena, and was correct for thermal radiation at lower temperatures.

At the time Planck took up the problem of thermal radiation, experimenters in Germany were engaged in measuring the radiation emitted by hot objects with ever-increasing precision, confirming the discrepancy between theory and reality, and falsifying several attempts to explain the measurements. In December 1900, Planck presented his new theory of black body radiation and what is now called Planck's Law at a conference in Berlin. Written in modern notation, his formula for the energy emitted by a body of temperature T at frequency ν is:

This equation not only correctly predicted the results measured in the laboratories, it avoided the ultraviolet catastrophe, as it predicted an absolute cutoff of the highest frequency radiation which could be emitted based upon an object's temperature. This meant that the absorption and re-emission of radiation in the closed oven could never run away to infinity because no energy could be emitted above the limit imposed by the temperature.

Fine: the theory explained the measurements. But what did it mean? More than a century later, we're still trying to figure that out.

Planck modeled the walls of the oven as a series of resonators, but unlike earlier theories in which each could emit energy at any frequency, he constrained them to produce discrete chunks of energy with a value determined by the frequency emitted. This had the result of imposing a limit on the frequency due to the available energy. While this assumption yielded the correct result, Planck, deeply steeped in the nineteenth century tradition of the continuum, did not initially suggest that energy was actually emitted in discrete packets, considering this aspect of his theory “a purely formal assumption.” Planck's 1900 paper generated little reaction: it was observed to fit the data, but the theory and its implications went over the heads of most physicists.

In 1905, in his capacity as editor of Annalen der Physik, he read and approved the publication of Einstein's paper on the photoelectric effect, which explained another physics puzzle by assuming that light was actually emitted in discrete bundles with an energy determined by its frequency. But Planck, whose equation manifested the same property, wasn't ready to go that far. As late as 1913, he wrote of Einstein, “That he might sometimes have overshot the target in his speculations, as for example in his light quantum hypothesis, should not be counted against him too much.” Only in the 1920s did Planck fully accept the implications of his work as embodied in the emerging quantum theory.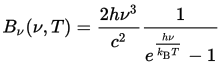

The equation for Planck's Law contained two new fundamental physical constants: Planck's constant (h) and Boltzmann's constant (k_B). (Boltzmann's constant was named in memory of Ludwig Boltzmann, the pioneer of statistical mechanics, who committed suicide in 1906. The constant was first introduced by Planck in his theory of thermal radiation.) Planck realised that these new constants, which related the worlds of the very large and very small, together with other physical constants such as the speed of light (c), the gravitational constant (G), and the Coulomb constant (k_e), allowed defining a system of units for quantities such as length, mass, time, electric charge, and temperature which were truly fundamental: derived from the properties of the universe we inhabit, and therefore comprehensible to intelligent beings anywhere in the universe. Most systems of measurement are derived from parochial anthropocentric quantities such as the temperature of somebody's armpit or the supposed distance from the north pole to the equator. Planck's natural units have no such dependencies, and when one does physics using them, equations become simpler and more comprehensible. The magnitudes of the Planck units are so far removed from the human scale they're unlikely to find any application outside theoretical physics (imagine speed limit signs expressed in a fraction of the speed of light, or road signs giving distances in Planck lengths of 1.62×10⁻³⁵ metres), but they reflect the properties of the universe and may indicate the limits of our ability to understand it (for example, it may not be physically meaningful to speak of a distance smaller than the Planck length or an interval shorter than the Planck time [5.39×10⁻⁴⁴ seconds]).

Planck's life was long and productive, and he enjoyed robust health (he continued his long hikes in the mountains into his eighties), but was marred by tragedy. His first wife, Marie, died of tuberculosis in 1909. He outlived four of his five children. His son Karl was killed in 1916 in World War I. His two daughters, Grete and Emma, both died in childbirth, in 1917 and 1919. His son and close companion Erwin, who survived capture and imprisonment by the French during World War I, was arrested and executed by the Nazis in 1945 for suspicion of involvement in the Stauffenberg plot to assassinate Hitler. (There is no evidence Erwin was a part of the conspiracy, but he was anti-Nazi and knew some of those involved in the plot.)

Planck was repulsed by the Nazis, especially after a private meeting with Hitler in 1933, but continued in his post as the head of the Kaiser Wilhelm Society until 1937. He considered himself a German patriot and never considered emigrating (and doubtless his being 75 years old when Hitler came to power was a consideration). He opposed and resisted the purging of Jews from German scientific institutions and the campaign against “Jewish science”, but when ordered to dismiss non-Aryan members of the Kaiser Wilhelm Society, he complied. When Heisenberg approached him for guidance, he said, “You have come to get my advice on political questions, but I am afraid I can no longer advise you. I see no hope of stopping the catastrophe that is about to engulf all our universities, indeed our whole country. … You simply cannot stop a landslide once it has started.”

Planck's house near Berlin was destroyed in an Allied bombing raid in February 1944, and with it a lifetime of his papers, photographs, and correspondence. (He and his second wife Marga had evacuated to Rogätz in 1943 to escape the raids.) As a result, historians have only limited primary sources from which to work, and the present book does an excellent job of recounting the life and science of a man whose work laid part of the foundations of twentieth century science.

January 2017 

Callender, Craig and Nick Huggett, eds. Physics Meets Philosophy at the Planck Scale. Cambridge: Cambridge University Press, 2001. ISBN 0-521-66445-4.

June 2001 

Carr, Bernard, ed. Universe or Multiverse? Cambridge: Cambridge University Press, 2007. ISBN 0-521-84841-5.

Before embarking upon his ultimately successful quest to discover the laws of planetary motion, Johannes Kepler tried to explain the sizes of the orbits of the planets from first principles: developing a mathematical model of the orbits based upon nested Platonic solids. Since, at the time, the solar system was believed by most to be the entire universe (with the fixed stars on a sphere surrounding it), it seemed plausible that the dimensions of the solar system would be fixed by fundamental principles of science and mathematics. Even though he eventually rejected his model as inaccurate, he never completely abandoned it—it was for later generations of astronomers to conclude that there is nothing fundamental whatsoever about the structure of the solar system: it is simply a contingent product of the history of its condensation from the solar nebula, and could have been entirely different. With the discovery of planets around other stars in the late twentieth century, we now know that not only do planetary systems vary widely, many are substantially more weird than most astronomers or even science fiction writers would have guessed.

Since the completion of the Standard Model of particle physics in the 1970s, a major goal of theoretical physicists has been to derive, from first principles, the values of the more than twenty-five “free parameters” of the Standard Model (such as the masses of particles, relative strengths of forces, and mixing angles). At present, these values have to be measured experimentally and put into the theory “by hand”, and there is no accepted physical explanation for why they have the values they do. Further, many of these values appear to be “fine-tuned” to allow the existence of life in the universe (or at least, life which resembles ourselves)—a tiny change, for example, in the mass ratio of the up and down quarks and the electron would result in a universe with no heavy elements or chemistry; it's hard to imagine any form of life which could be built out of just protons or neutrons. The emergence of a Standard Model of cosmology has only deepened the mystery, adding additional apparently fine-tunings to the list. Most stunning is the cosmological constant, which appears to have a nonzero value which is 124 orders of magnitude smaller than predicted from a straightforward calculation from quantum physics.

One might take these fine-tunings as evidence of a benevolent Creator (which is, indeed, discussed in chapters 25 and 26 of this book), or of our living in a simulation crafted by a clever programmer intent on optimising its complexity and degree of interestingness (chapter 27). But most physicists shy away from such deus ex machina and “we is in machina” explanations and seek purely physical reasons for the values of the parameters we measure.

Now let's return for a moment to Kepler's attempt to derive the orbits of the planets from pure geometry. The orbit of the Earth appears, in fact, fine-tuned to permit the existence of life. Were it more elliptical, or substantially closer to or farther from the Sun, persistent liquid water on the surface would not exist, as seems necessary for terrestrial life. The apparent fine-tuning can be explained, however, by the high probability that the galaxy contains a multitude of planetary systems of every possible variety, and such a large ensemble is almost certain to contain a subset (perhaps small, but not void) in which an earthlike planet is in a stable orbit within the habitable zone of its star. Since we can only have evolved and exist in such an environment, we should not be surprised to find ourselves living on one of these rare planets, even though such environments represent an infinitesimal fraction of the volume of the galaxy and universe.

As efforts to explain the particle physics and cosmological parameters have proved frustrating, and theoretical investigations into cosmic inflation and string theory have suggested that the values of the parameters may have simply been chosen at random by some process, theorists have increasingly been tempted to retrace the footsteps of Kepler and step back from trying to explain the values we observe, and instead view them, like the masses and the orbits of the planets, as the result of an historical process which could have produced very different results. The apparent fine-tuning for life is like the properties of the Earth's orbit—we can only measure the parameters of a universe which permits us to exist! If they didn't, we wouldn't be here to do the measuring.

But note that like the parallel argument for the fine-tuning of the orbit of the Earth, this only makes sense if there are a multitude of actually existing universes with different random settings of the parameters, just as only a large ensemble of planetary systems can contain a few like the one in which we find ourselves. This means that what we think of as our universe (everything we can observe or potentially observe within the Hubble volume) is just one domain in a vastly larger “multiverse”, most or all of which may remain forever beyond the scope of scientific investigation.

Now such a breathtaking concept provides plenty for physicists, cosmologists, philosophers, and theologians to chew upon, and macerate it they do in this thick (517 page), heavy (1.2 kg), and expensive (USD 85) volume, which is drawn from papers presented at conferences held between 2001 and 2005. Contributors include two Nobel laureates (Steven Weinberg and Frank Wilczek), and just about everybody else prominent in the multiverse debate, including Martin Rees, Stephen Hawking, Max Tegmark, Andrei Linde, Alexander Vilenkin, Renata Kallosh, Leonard Susskind, James Hartle, Brandon Carter, Lee Smolin, George Ellis, Nick Bostrom, John Barrow, Paul Davies, and many more. The editor's goal was that the papers be written for the intelligent layman: like articles in the pre-dumbed-down Scientific American or “front of book” material in Nature or Science. In fact, the chapters vary widely in technical detail and difficulty; if you don't follow this stuff closely, your eyes may glaze over in some of the more equation-rich chapters.

This book is far from a cheering section for multiverse theories: both sides are presented and, in fact, the longest chapter is that of Lee Smolin, which deems the anthropic principle and anthropic arguments entirely nonscientific. Many of these papers are available in preliminary form for free on the arXiv preprint server; if you can obtain a list of the chapter titles and authors from the book, you can read most of the content for free. Renata Kallosh's chapter contains an excellent example of why one shouldn't blindly accept the recommendations of a spelling checker. On p. 205, she writes “…the gaugino condensate looks like a fractional instant on effect…”—that's supposed to be “instanton”!

August 2007 

Carroll, Sean. From Eternity to Here. New York: Dutton, 2010. ISBN 978-0-525-95133-9.

The nature of time has perplexed philosophers and scientists from the ancient Greeks (and probably before) to the present day. Despite two and half millennia of reflexion upon the problem and spectacular success in understanding many other aspects of the universe we inhabit, not only has little progress been made on the question of time, but to a large extent we are still puzzling over the same problems which vexed thinkers in the time of Socrates: Why does there seem to be an inexorable arrow of time which can be perceived in physical processes (you can scramble an egg, but just try to unscramble one)? Why do we remember the past, but not the future? Does time flow by us, living in an eternal present, or do we move through time? Do we have free will, or is that an illusion and is the future actually predestined? Can we travel to the past or to the future? If we are typical observers in an eternal or very long-persisting universe, why do we find ourselves so near its beginning (the big bang)?

Indeed, what we have learnt about time makes these puzzles even more enigmatic. For it appears, based both on theory and all experimental evidence to date, that the microscopic laws of physics are completely reversible in time: any physical process can (and does) go in both the forward and reverse time directions equally well. (Actually, it's a little more complicated than that: just reversing the direction of time does not yield identical results, but simultaneously reversing the direction of time [T], interchanging left and right [parity: P], and swapping particles for antiparticles [charge: C] yields identical results under the so-called “CPT” symmetry which, as far is known, is absolute. The tiny violation of time reversal symmetry by itself in weak interactions seems, to most physicists, inadequate to explain the perceived unidirectional arrow of time, although some disagree.)

In this book, the author argues that the way in which we perceive time here and now (whatever “now” means) is a direct consequence of the initial conditions which obtained at the big bang—the beginning of time, and the future state into which the universe is evolving—eternity. Whether or not you agree with the author's conclusions, this book is a tour de force popular exposition of thermodynamics and statistical mechanics, which provides the best intuitive grasp of these concepts of any non-technical book I have yet encountered. The science and ideas which influenced thermodynamics and its practical and philosophical consequences are presented in a historical context, showing how in many cases phenomenological models were successful in grasping the essentials of a physical process well before the actual underlying mechanisms were understood (which is heartening to those trying to model the very early universe absent a theory of quantum gravity).

Carroll argues that the Second Law of Thermodynamics entirely defines the arrow of time. Closed systems (and for the purpose of the argument here we can consider the observable universe as such a system, although it is not precisely closed: particles enter and leave our horizon as the universe expands and that expansion accelerates) always evolve from a state of lower probability to one of higher probability: the “entropy” of a system is (sloppily stated) a measure of the probability of finding the system in a given macroscopically observable state, and over time the entropy always stays the same or increases; except for minor fluctuations, the entropy increases until the system reaches equilibrium, after which it simply fluctuates around the equilibrium state with essentially no change in its coarse-grained observable state. What we perceive as the arrow of time is simply systems evolving from less probable to more probable states, and since they (in isolation) never go the other way, we naturally observe the arrow of time to be universal.

Look at it this way—there are vastly fewer configurations of the atoms which make up an egg as produced by a chicken: shell outside, yolk in the middle, and white in between, as there are for the same egg scrambled in the pan with the fragments of shell discarded in the poubelle. There are an almost inconceivable number of ways in which the atoms of the yolk and white can mix to make the scrambled egg, but far fewer ways they can end up neatly separated inside the shell. Consequently, if we see a movie of somebody unscrambling an egg, the white and yolk popping up from the pan to be surrounded by fragments which fuse into an unbroken shell, we know some trickster is running the film backward: it illustrates a process where the entropy dramatically decreases, and that never happens in the real world. (Or, more precisely, its probability of happening anywhere in the universe in the time since the big bang is “beyond vanishingly small”.)

Now, once you understand these matters, as you will after reading the pellucid elucidation here, it all seems pretty straightforward: our universe is evolving, like all systems, from lower entropy to higher entropy, and consequently it's only natural that we perceive that evolution as the passage of time. We remember the past because the process of storing those memories increases the entropy of the universe; we cannot remember the future because we cannot predict the precise state of the coarse-grained future from that of the present, simply because there are far more possible states in the future than at the present. Seems reasonable, right?

Well, up to a point, Lord Copper. The real mystery, to which Roger Penrose and others have been calling attention for some years, is not that entropy is increasing in our universe, but rather why it is presently so low compared to what it might be expected to be in a universe in a randomly chosen configuration, and further, why it was so absurdly low in the aftermath of the big bang. Given the initial conditions after the big bang, it is perfectly reasonable to expect the universe to have evolved to something like its present state. But this says nothing at all about why the big bang should have produced such an incomprehensibly improbable set of initial conditions.

If you think about entropy in the usual thermodynamic sense of gas in a box, the evolution of the universe seems distinctly odd. After the big bang, the region which represents today's observable universe appears to have been a thermalised system of particles and radiation very near equilibrium, and yet today we see nothing of the sort. Instead, we see complex structure at scales from molecules to superclusters of galaxies, with vast voids in between, and stars profligately radiating energy into space with a temperature less than three degrees above absolute zero. That sure doesn't look like entropy going down: it's more like your leaving a pot of tepid water on the counter top overnight and, the next morning, finding a village of igloos surrounding a hot spring. I mean, it could happen, but how probable is that?

It's gravity that makes the difference. Unlike all of the other forces of nature, gravity always attracts. This means that when gravity is significant (which it isn't in a steam engine or pan of water), a gas at thermal equilibrium is actually in a state of very low entropy. Any small compression or rarefaction in a region will cause particles to be gravitationally attracted to volumes with greater density, which will in turn reinforce the inhomogeneity, which will amplify the gravitational attraction. The gas at thermal equilibrium will, then, unless it is perfectly homogeneous (which quantum and thermal fluctuations render impossible) collapse into compact structures separated by voids, with the entropy increasing all the time. Voilà galaxies, stars, and planets.

As sources of energy are exhausted, gravity wins in the end, and as structures compact ever more, entropy increasing apace, eventually the universe is filled only with black holes (with vastly more entropy than the matter and energy that fell into them) and cold dark objects. But wait, there's more! The expansion of the universe is accelerating, so any structures which are not gravitationally bound will eventually disappear over the horizon and the remnants (which may ultimately decay into a gas of unbound particles, although the physics of this remains speculative) will occupy a nearly empty expanding universe (absurd as this may sound, this de Sitter space is an exact solution to Einstein's equations of General Relativity). This, the author argues, is the highest entropy state of matter and energy in the presence of gravitation, and it appears from current observational evidence that that's indeed where we're headed.

So, it's plausible the entire evolution of the universe from the big bang into the distant future increases entropy all the way, and hence there's no mystery why we perceive an arrow of time pointing from the hot dense past to cold dark eternity. But doggone it, we still don't have a clue why the big bang produced such low entropy! The author surveys a number of proposed explanations, some of which invoke fine-tuning with no apparent physical explanations, summon an enormous (or infinite) “multiverse” of all possibilities and argue that among such an ensemble, we find ourselves in one of the vanishingly small fraction of universes like our own because observers like ourselves couldn't exist in all the others (the anthropic argument), or that the big bang was not actually the beginning and that some dynamical process which preceded the big bang (which might then be considered a “big bounce”) forced the initial conditions into a low entropy state. There are many excellent arguments against these proposals, which are clearly presented. The author's own favourite, which he concedes is as speculative as all the others, is that de Sitter space is unstable against a quantum fluctuation which nucleates a disconnected bubble universe in which entropy is initially low. The process of nucleation increases entropy in the multiverse, and hence there is no upper bound at all on entropy, with the multiverse eternal in past and future, and entropy increasing forever without bound in the future and decreasing without bound in the past.

(If you're a regular visitor here, you know what's coming, don't you?) Paging friar Ockham! We start out having discovered yet another piece of evidence for what appears to be a fantastically improbable fine-tuning of the initial conditions of our universe. The deeper we investigate this, the more mysterious it appears, as we discover no reason in the dynamical laws of physics for the initial conditions to be have been so unlikely among the ensemble of possible initial conditions. We are then faced with the “trichotomy” I discussed regarding the origin of life on Earth: chance (it just happened to be that way, or it was every possible way, and we, tautologically, live in one of the universes in which we can exist), necessity (some dynamical law which we haven't yet figured out caused the initial conditions to be the way we observe them to have been), or (and here's where all the scientists turn their backs upon me, snuff the candles, and walk away) design. Yes, design. Suppose (and yes, I know, I've used this analogy before and will certainly do so again) you were a character in a video game who somehow became sentient and began to investigate the universe you inhabited. As you did, you'd discover there were distinct regularities which governed the behaviour of objects and their interactions. As you probed deeper, you might be able to access the machine code of the underlying simulation (or at least get a glimpse into its operation by running precision experiments). You would discover that compared to a random collection of bits of the same length, it was in a fantastically improbable configuration, and you could find no plausible way that a random initial configuration could evolve into what you observe today, especially since you'd found evidence that your universe was not eternally old but rather came into being at some time in the past (when, say, the game cartridge was inserted).

What would you conclude? Well, if you exclude the design hypothesis, you're stuck with supposing that there may be an infinity of universes like yours in all random configurations, and you observe the one you do because you couldn't exist in all but a very few improbable configurations of that ensemble. Or you might argue that some process you haven't yet figured out caused the underlying substrate of your universe to assemble itself, complete with the copyright statement and the Microsoft security holes, from a generic configuration beyond your ability to observe in the past. And being clever, you'd come up with persuasive arguments as to how these most implausible circumstances might have happened, even at the expense of invoking an infinity of other universes, unobservable in principle, and an eternity of time, past and present, in which events could play out.

Or, you might conclude from the quantity of initial information you observed (which is identical to low initial entropy) and the improbability of that configuration having been arrived at by random processes on any imaginable time scale, that it was put in from the outside by an intelligent designer: you might call Him or Her the Programmer, and some might even come to worship this being, outside the observable universe, which is nonetheless responsible for its creation and the wildly improbable initial conditions which permit its inhabitants to exist and puzzle out their origins.

Suppose you were running a simulation of a universe, and to win the science fair you knew you'd have to show the evolution of complexity all the way from the get-go to the point where creatures within the simulation started to do precision experiments, discover curious fine-tunings and discrepancies, and begin to wonder…? Would you start your simulation at a near-equilibrium condition? Only if you were a complete idiot—nothing would ever happen—and whatever you might say about post-singularity super-kids, they aren't idiots (well, let's not talk about the music they listen to, if you can call that music). No, you'd start the simulation with extremely low entropy, with just enough inhomogeneity that gravity would get into the act and drive the emergence of hierarchical structure. (Actually, if you set up quantum mechanics the way we observe it, you wouldn't have to put in the inhomogeneity; it will emerge from quantum fluctuations all by itself.) And of course you'd fine tune the parameters of the standard model of particle physics so your universe wouldn't immediately turn entirely into neutrons, diprotons, or some other dead end. Then you'd sit back, turn up the volume on the MultIversePod, and watch it run. Sure 'nuff, after a while there'd be critters trying to figure it all out, scratching their balding heads, and wondering how it came to be that way. You would be most amused as they excluded your existence as a hypothesis, publishing theories ever more baroque to exclude the possibility of design. You might be tempted to….

Fortunately, this chronicle does not publish comments. If you're sending them from the future, please use the antitelephone.

(The author discusses this “simulation argument” in endnote 191. He leaves it to the reader to judge its plausibility, as do I. I remain on the record as saying, “more likely than not”.)

Whatever you may think about the Big Issues raised here, if you've never experienced the beauty of thermodynamics and statistical mechanics at a visceral level, this is the book to read. I'll bet many engineers who have been completely comfortable with computations in “thermogoddamics” for decades finally discover they “get it” after reading this equation-free treatment aimed at a popular audience.

February 2010 

Carroll, Sean. The Particle at the End of the Universe. New York: Dutton, 2012. ISBN 978-0-525-95359-3.

I believe human civilisation is presently in a little-perceived race between sinking into an entropic collapse, extinguishing liberty and individual initiative, and a technological singularity which will simply transcend all of the problems we presently find so daunting and intractable. If things end badly, our descendants may look upon our age as one of extravagance, where vast resources were expended in a quest for pure knowledge without any likelihood of practical applications.

Thus, the last decade has seen the construction of what is arguably the largest and most complicated machine ever built by our species, the Large Hadron Collider (LHC), to search for and determine the properties of elementary particles: the most fundamental constituents of the universe we inhabit. This book, accessible to the intelligent layman, recounts the history of the quest for the components from which everything in the universe is made, the ever more complex and expensive machines we've constructed to explore them, and the intricate interplay between theory and experiment which this enterprise has entailed.

At centre stage in this narrative is the Higgs particle, first proposed in 1964 as accounting for the broken symmetry in the electroweak sector (as we'd now say), which gives mass to the W and Z bosons, accounting for the short range of the weak interaction and the mass of the electron. (It is often sloppily said that the Higgs mechanism explains the origin of mass. In fact, as Frank Wilczek explains in The Lightness of Being [March 2009], around 95% of all hadronic mass in the universe is pure E=mc² wiggling of quarks and gluons within particles in the nucleus.) Still, the Higgs is important—if it didn't exist the particles we're made of would all be massless, travel at the speed of light, and never aggregate into stars, planets, physicists, or most importantly, computer programmers. On the other hand, there wouldn't be any politicians.

The LHC accelerates protons (the nuclei of hydrogen, which delightfully come from a little cylinder of hydrogen gas shown on p. 310, which contains enough to supply the LHC with protons for about a billion years) to energies so great that these particles, when they collide, have about the same energy as a flying mosquito. You might wonder why the LHC collides protons with protons rather than with antiprotons as the Tevatron did. While colliding protons with antiprotons allows more of the collision energy to go into creating new particles, the LHC's strategy of very high luminosity (rate of collisions) would require creation of far more antiprotons than its support facilities could produce, hence the choice of proton-proton collisions. While the energy of individual particles accelerated by the LHC is modest from our macroscopic perspective, the total energy of the beam circulating around the accelerator is intimidating: a full beam dump would suffice to melt a ton of copper. Be sure to step aside should this happen.

Has the LHC found the Higgs? Probably—the announcement on July 4th, 2012 by the two detector teams reported evidence for a particle with properties just as expected for the Higgs, so if it turned out to be something else, it would be a big surprise (but then Nature never signed a contract with scientists not to perplex them with misdirection). Unlike many popular accounts, this book looks beneath the hood and explores just how difficult it is to tease evidence for a new particle from the vast spray of debris that issues from particle collisions. It isn't like a little ball with an “h” pops out and goes “bing” in the detector: in fact, a newly produced Higgs particle decays in about 10⁻²² seconds, even faster than assets entrusted to the management of Goldman Sachs. The debris which emerges from the demise of a Higgs particle isn't all that different from that produced by many other standard model events, so the evidence for the Higgs is essentially a “bump” in the rate of production of certain decay signatures over that expected from the standard model background (sources expected to occur in the absence of the Higgs). These, in turn, require a tremendous amount of theoretical and experimental input, as well as massive computer calculations to evaluate; once you begin to understand this, you'll appreciate that the distinction between theory and experiment in particle physics is more fluid than you might have imagined.

This book is a superb example of popular science writing, and its author has distinguished himself as a master of the genre. He doesn't pull any punches: after reading this book you'll understand, at least at a conceptual level, broken symmetries, scalar fields, particles as excitations of fields, and the essence of quantum mechanics (as given by Aatish Bhatia on Twitter), “Don't look: waves. Look: particles.”

January 2013 

Charpak, Georges et Richard L. Garwin. Feux follets et champignons nucléaires. Paris: Odile Jacob, [1997] 2000. ISBN 978-2-7381-0857-9.

Georges Charpak won the Nobel Prize in Physics in 1992, and was the last person, as of this writing, to have won an unshared Physics Nobel. Richard Garwin is a quintessential “defence intellectual”: he studied under Fermi, did the detailed design of Ivy Mike, the first thermonuclear bomb, has been a member of Jason and adviser on issues of nuclear arms control and disarmament for decades, and has been a passionate advocate against ballistic missile defence and for reducing the number of nuclear warheads and the state of alert of strategic nuclear forces.

In this book the authors, who do not agree on everything and take the liberty to break out from the main text on several occasions to present their individual viewpoints, assess the state of nuclear energy—civil and military—at the turn of the century and try to chart a reasonable path into the future which is consistent with the aspirations of people in developing countries, the needs of a burgeoning population, and the necessity of protecting the environment both from potential risks from nuclear technology but also the consequences of not employing it as a source of energy. (Even taking Chernobyl into account, the total radiation emitted by coal-fired power plants is far greater than that of all nuclear stations combined: coal contains thorium, and when it is burned, it escapes in flue gases or is captured and disposed of in landfills. And that's not even mentioning the carbon dioxide emitted by burning fossil fuels.)

The reader of this book will learn a great deal about the details of nuclear energy: perhaps more than some will have the patience to endure. I made it through, and now I really understand, for the first time, why light water reactors have a negative thermal coefficient: as the core gets hotter, the U-238 atoms are increasingly agitated by the heat, and consequently are more likely due to Doppler shift to fall into one of the resonances where their neutron absorption is dramatically enhanced.

Charpak and Garwin are in complete agreement that civil nuclear power should be the primary source of new electrical generation capacity until and unless something better (such as fusion) comes along. They differ strongly on the issue of fuel cycle and waste management: Charpak argues for the French approach of reprocessing spent fuel, extracting the bred plutonium, and burning it in power reactors in the form of mixed oxide (MOX) fuel. Garwin argues for the U.S. approach of a once-through fuel cycle, with used fuel buried, its plutonium energy content discarded in the interest of “economy”. Charpak points out that the French approach drastically reduces the volume of nuclear waste to be buried, and observes that France does not have a Nevada in which to bury it.

Both authors concur that breeder reactors will eventually have a rôle to play in nuclear power generation. Not only do breeders multiply the energy which can be recovered from natural uranium by a factor of fifty, they can be used to “burn up” many of the radioactive waste products of conventional light water reactors. Several next-generation reactor concepts are discussed, including Carlo Rubbia's energy amplifier, in which the core is inherently subcritical, and designs for more conventional reactors which are inherently safe in the event of loss of control feedback or cooling. They conclude, however, that further technology maturation is required before breeders enter into full production use and that, in retrospect, Superphénix was premature.

The last third of the book is devoted to nuclear weapons and the prospects for reducing the inventory of declared nuclear powers, increasing stability, and preventing proliferation. There is, as you would expect from Garwin, a great deal of bashing the concept of ballistic missile defence (“It can't possibly work, and if it did it would be bad”). This is quite dated, as many of the arguments and the lengthy reprinted article date from the mid 1980s when the threat was a massive “war-gasm” salvo launch of thousands of ICBMs from the Soviet Union, not one or two missiles from a rogue despot who's feeling “ronery”. The authors quite reasonably argue that current nuclear force levels are absurd, and that an arsenal about the size of France's (on the order of 500 warheads) should suffice for any conceivable deterrent purpose. They dance around the option of eliminating nuclear arms entirely, and conclude that such a goal is probably unachievable in a world in which such a posture would create an incentive for a rogue state to acquire even one or two weapons. They suggest a small deterrent force operated by an international authority—good luck with that!

This is a thoughtful book which encourages rational people to think for themselves about the energy choices facing humanity in the coming decades. It counters emotional appeals and scare trigger words with the best antidote: numbers. Numbers which demonstrate, for example, that the inherent radiation of atoms in the human body (mostly C-14 and K-40) and the variation in natural background radiation from one place to another on Earth is vastly greater than the dose received from all kinds of nuclear technology. The Chernobyl and Three Mile Island accidents are examined in detail, and the lessons learnt for safely operating nuclear power stations are explored. I found the sections on nuclear weapons weaker and substantially more dated. Although the book was originally published well after the collapse of the Soviet Union, the perspective is still very much that of superpower confrontation, not the risk of proliferation to rogue states and terrorist groups. Certainly, responsibly disposing of the excess fissile material produced by the superpowers in their grotesquely hypertrophied arsenals (ideally by burning it up in civil power reactors, as opposed to insanely dumping it into a hole in the ground to remain a risk for hundreds of thousands of years, as some “green” advocates urge) is an important way to reduce the risks of proliferation, but events subsequent to the publication of this book have shown that states are capable of mounting their own indigenous nuclear weapons programs under the eyes of international inspectors. Will an “international community” which is incapable of stopping such clandestine weapons programs have any deterrent credibility even if armed with its own nuclear-tipped missiles?

An English translation of this book, entitled Megawatts and Megatons, is available.

September 2009 

Charpak, Georges et Henri Broch. Devenez sorciers, devenez savants. Paris: Odile Jacob, 2002. ISBN 2-7381-1093-2.

June 2002 

Dyson, Freeman J. The Sun, the Genome, and the Internet. Oxford: Oxford University Press, 1999. ISBN 0-19-513922-4.

The text in this book is set in a hideous flavour of the Adobe Caslon font in which little curlicue ligatures connect the letter pairs “ct” and “st” and, in addition, the “ligatures” for “ff”, “fi”, “fl”, and “ft” lop off most of the bar of the “f”, leaving it looking like a droopy “l”. This might have been elegant for chapter titles, but it's way over the top for body copy. Dyson's writing, of course, more than redeems the bad typography, but you gotta wonder why we couldn't have had the former without the latter.

September 2003 

Einstein, Albert. Autobiographical Notes. Translated and edited by Paul Arthur Schilpp. La Salle, Illinois: Open Court, [1949] 1996. ISBN 0-8126-9179-2.

July 2001 

Einstein, Albert, Hanock Gutfreund, and Jürgen Renn. The Road to Relativity. Princeton: Princeton University Press, 2015. ISBN 978-0-691-16253-9.

One hundred years ago, in 1915, Albert Einstein published the final version of his general theory of relativity, which extended his 1905 special theory to encompass accelerated motion and gravitation. It replaced the Newtonian concept of a “gravitational force” acting instantaneously at a distance through an unspecified mechanism with the most elegant of concepts: particles not under the influence of an external force move along spacetime geodesics, the generalisation of straight lines, but the presence of mass-energy curves spacetime, which causes those geodesics to depart from straight lines when observed at a large scale.

For example, in Newton's conception of gravity, the Earth orbits the Sun because the Sun exerts a gravitational force upon the Earth which pulls it inward and causes its motion to depart from a straight line. (The Earth also exerts a gravitational force upon the Sun, but because the Sun is so much more massive, this can be neglected to a first approximation.) In general relativity there is no gravitational force. The Earth is moving in a straight line in spacetime, but because the Sun curves spacetime in its vicinity this geodesic traces out a helix in spacetime which we perceive as the Earth's orbit.

Now, if this were a purely qualitative description, one could dismiss it as philosophical babble, but Einstein's theory provided a precise description of the gravitational field and the motion of objects within it and, when the field strength is strong or objects are moving very rapidly, makes different predictions than Newton's theory. In particular, Einstein's theory predicted that the perihelion of the orbit of Mercury would rotate around the Sun more rapidly than Newton's theory could account for, that light propagating near the limb of the Sun or other massive bodies would be bent through twice the angle Newton's theory predicted, and that light from the Sun or other massive stars would be red-shifted when observed from a distance. In due course all of these tests have been found to agree with the predictions of general relativity. The theory has since been put to many more precise tests and no discrepancy with experiment has been found. For a theory which is, once you get past the cumbersome mathematical notation in which it is expressed, simple and elegant, its implications are profound and still being explored a century later. Black holes, gravitational lensing, cosmology and the large-scale structure of the universe, gravitomagnetism, and gravitational radiation are all implicit in Einstein's equations, and exploring them are among the frontiers of science a century hence.

Unlike Einstein's original 1905 paper on special relativity, the 1915 paper, titled “Die Grundlage der allgemeinen Relativitätstheorie” (“The Foundation of General Relativity”) is famously difficult to comprehend and baffled many contemporary physicists when it was published. Almost half is a tutorial for physicists in Riemann's generalised multidimensional geometry and the tensor language in which it is expressed. The balance of the paper is written in this notation, which can be forbidding until one becomes comfortable with it.

That said, general relativity can be understood intuitively the same way Einstein began to think about it: through thought experiments. First, imagine a person in a stationary elevator in the Earth's gravitational field. If the elevator cable were cut, while the elevator was in free fall (and before the sudden stop), no experiment done within the elevator could distinguish between the state of free fall within Earth's gravity and being in deep space free of gravitational fields. (Conversely, no experiment done in a sufficiently small closed laboratory can distinguish it being in Earth's gravitational field from being in deep space accelerating under the influence of a rocket with the same acceleration as Earth's gravity.) (The “sufficiently small” qualifier is to eliminate the effects of tides, which we can neglect at this level.)

The second thought experiment is a bit more subtle. Imagine an observer at the centre of a stationary circular disc. If the observer uses rigid rods to measure the radius and circumference of the disc, he will find the circumference divided by the radius to be 2π, as expected from the Euclidean geometry of a plane. Now set the disc rotating and repeat the experiment. When the observer measures the radius, it will be as before, but at the circumference the measuring rod will be contracted due to its motion according to special relativity, and the circumference, measured by the rigid rod, will be seen to be larger. Now, when the circumference is divided by the radius, a ratio greater than 2π will be found, indicating that the space being measured is no longer Euclidean: it is curved. But the only difference between a stationary disc and one which is rotating is that the latter is in acceleration, and from the reasoning of the first thought experiment there is no difference between acceleration and gravity. Hence, gravity must bend spacetime and affect the paths of objects (geodesics) within it.

Now, it's one thing to have these kinds of insights, and quite another to puzzle out the details and make all of the mathematics work, and this process occupied Einstein for the decade between 1905 and 1915, with many blind alleys. He eventually came to understand that it was necessary to entirely discard the notion of any fixed space and time, and express the equations of physics in a way which was completely independent of any co-ordinate system. Only this permitted the metric structure of spacetime to be completely determined by the mass and energy within it.

This book contains a facsimile reproduction of Einstein's original manuscript, now in the collection of the Hebrew University of Jerusalem. The manuscript is in Einstein's handwriting which, if you read German, you'll have no difficulty reading. Einstein made many edits to the manuscript before submitting it for publication, and you can see them all here. Some of the hand-drawn figures in the manuscript have been cut out by the publisher to be sent to an illustrator for preparation of figures for the journal publication. Parallel to the manuscript, the editors describe the content and the historical evolution of the concepts discussed therein. There is a 36 page introduction which describes the background of the theory and Einstein's quest to discover it and the history of the manuscript. An afterword provides an overview of general relativity after Einstein and brief biographies of principal figures involved in the development and elaboration of the theory. The book concludes with a complete English translation of Einstein's two papers given in the manuscript.

This is not the book to read if you're interested in learning general relativity; over the last century there have been great advances in mathematical notation and pedagogy, and a modern text is the best resource. But, in this centennial year, this book allows you to go back to the source and understand the theory as Einstein presented it, after struggling for so many years to comprehend it. The supplemental material explains the structure of the paper, the essentials of the theory, and how Einstein came to develop it.

October 2015 

Farmelo, Graham. The Strangest Man. New York: Basic Books, 2009. ISBN 978-0-465-02210-6.

Paul Adrien Maurice Dirac was born in 1902 in Bristol, England. His father, Charles, was a Swiss-French immigrant who made his living as a French teacher at a local school and as a private tutor in French. His mother, Florence (Flo), had given up her job as a librarian upon marrying Charles. The young Paul and his older brother Felix found themselves growing up in a very unusual, verging upon bizarre, home environment. Their father was as strict a disciplinarian at home as in the schoolroom, and spoke only French to his children, requiring them to answer in that language and abruptly correcting them if they committed any faute de français. Flo spoke to the children only in English, and since the Diracs rarely received visitors at home, before going to school Paul got the idea that men and women spoke different languages. At dinner time Charles and Paul would eat in the dining room, speaking French exclusively (with any error swiftly chastised) while Flo, Felix, and younger daughter Betty ate in the kitchen, speaking English. Paul quickly learned that the less he said, the fewer opportunities for error and humiliation, and he traced his famous reputation for taciturnity to his childhood experience.

(It should be noted that the only account we have of Dirac's childhood experience comes from himself, much later in life. He made no attempt to conceal the extent he despised his father [who was respected by his colleagues and acquaintances in Bristol], and there is no way to know whether Paul exaggerated or embroidered upon the circumstances of his childhood.)

After a primary education in which he was regarded as a sound but not exceptional pupil, Paul followed his brother Felix into the Merchant Venturers' School, a Bristol technical school ranked among the finest in the country. There he quickly distinguished himself, ranking near the top in most subjects. The instruction was intensely practical, eschewing Latin, Greek, and music in favour of mathematics, science, geometric and mechanical drawing, and practical skills such as operating machine tools. Dirac learned physics and mathematics with the engineer's eye to “getting the answer out” as opposed to finding the most elegant solution to the problem. He then pursued his engineering studies at Bristol University, where he excelled in mathematics but struggled with experiments.

Dirac graduated with a first-class honours degree in engineering, only to find the British economy in a terrible post-war depression, the worst economic downturn since the start of the Industrial Revolution. Unable to find employment as an engineer, he returned to Bristol University to do a second degree in mathematics, where it was arranged he could skip the first year of the program and pay no tuition fees. Dirac quickly established himself as the star of the mathematics programme, and also attended lectures about the enigmatic quantum theory.

His father had been working in the background to secure a position at Cambridge for Paul, and after cobbling together scholarships and a gift from his father, Dirac arrived at the university in October 1923 to pursue a doctorate in theoretical physics. Dirac would already have seemed strange to his fellow students. While most were scions of the upper class, classically trained, with plummy accents, Dirac knew no Latin or Greek, spoke with a Bristol accent, and approached problems as an engineer or mathematician, not a physicist. He had hoped to study Einstein's general relativity, the discovery of which had first interested him in theoretical physics, but his supervisor was interested in quantum mechanics and directed his work into that field.

It was an auspicious time for a talented researcher to undertake work in quantum theory. The “old quantum theory”, elaborated in the early years of the 20th century, had explained puzzles like the distribution of energy in heat radiation and the photoelectric effect, but by the 1920s it was clear that nature was much more subtle. For example, the original quantum theory failed to explain even the spectral lines of hydrogen, the simplest atom. Dirac began working on modest questions related to quantum theory, but his life was changed when he read Heisenberg's 1925 paper which is now considered one of the pillars of the new quantum mechanics. After initially dismissing the paper as overly complicated and artificial, he came to believe that it pointed the way forward, dismissing Bohr's concept of atoms like little solar systems in favour of a probability density function which gives the probability an electron will be observed in a given position. This represented not just a change in the model of the atom but the discarding entirely of models in favour of a mathematical formulation which permitted calculating what could be observed without providing any mechanism whatsoever explaining how it worked.

After reading and fully appreciating the significance of Heisenberg's work, Dirac embarked on one of the most productive bursts of discovery in the history of modern physics. Between 1925 and 1933 he published one foundational paper after another. His Ph.D. in 1926, the first granted by Cambridge for work in quantum mechanics, linked Heisenberg's theory to the classical mechanics he had learned as an engineer and provided a framework which made Heisenberg's work more accessible. Scholarly writing did not come easily to Dirac, but he mastered the art to such an extent that his papers are still read today as examples of pellucid exposition. At a time when many contributions to quantum mechanics were rough-edged and difficult to understand even by specialists, Dirac's papers were, in the words of Freeman Dyson, “like exquisitely carved marble statues falling out of the sky, one after another.”

In 1928, Dirac took the first step to unify quantum mechanics and special relativity in the Dirac equation. The consequences of this equation led Dirac to predict the existence of a positively-charged electron, which had never been observed. This was the first time a theoretical physicist had predicted the existence of a new particle. This “positron” was observed in debris from cosmic ray collisions in 1932. The Dirac equation also interpreted the spin (angular momentum) of particles as a relativistic phenomenon.

Dirac, along with Enrico Fermi, elaborated the statistics of particles with half-integral spin (now called “fermions”). The behaviour of ensembles of one such particle, the electron, is essential to the devices you use to read this article. He took the first steps toward a relativistic theory of light and matter and coined the name, “quantum electrodynamics”, for the field, but never found a theory sufficiently simple and beautiful to satisfy himself. He published The Principles of Quantum Mechanics in 1930, for many years the standard textbook on the subject and still read today. He worked out the theory of magnetic monopoles (not detected to this date) and speculated on the origin and possible links between large numbers in physics and cosmology.

The significance of Dirac's work was recognised at the time. He was elected a Fellow of the Royal Society in 1930, became the Lucasian Professor of Mathematics (Newton's chair) at Cambridge in 1932, and shared the Nobel Prize in Physics for 1933 with Erwin Schrödinger. After rejecting a knighthood because he disliked being addressed by his first name, he was awarded the Order of Merit in 1973. He is commemorated by a plaque in Westminster Abbey, close to that of Newton; the plaque bears his name and the Dirac equation, the only equation so honoured.

Many physicists consider Dirac the second greatest theoretical physicist of the 20th century, after Einstein. While Einstein produced great leaps of intellectual achievement in fields neglected by others, Dirac, working alone, contributed to the grand edifice of quantum mechanics, which occupied many of the most talented theorists of a generation. You have to dig a bit deeper into the history of quantum mechanics to fully appreciate Dirac's achievement, which probably accounts for his name not being as well known as it deserves.

There is much more to Dirac, all described in this extensively-documented scientific biography. While declining to join the British atomic weapons project during World War II because he refused to work as part of a collaboration, he spent much of the war doing consulting work for the project on his own, including inventing a new technique for isotope separation. (Dirac's process proved less efficient that those eventually chosen by the Manhattan project and was not used.) As an extreme introvert, nobody expected him to ever marry, and he astonished even his closest associates when he married the sister of his fellow physicist Eugene Wigner, Manci, a Hungarian divorcée with two children by her first husband. Manci was as extroverted as Dirac was reserved, and their marriage in 1937 lasted until Dirac's death in 1984. They had two daughters together, and lived a remarkably normal family life. Dirac, who disdained philosophy in his early years, became intensely interested in the philosophy of science later in life, even arguing that mathematical beauty, not experimental results, could best guide theorists to the best expression of the laws of nature.

Paul Dirac was a very complicated man, and this is a complicated and occasionally self-contradictory biography (but the contradiction is in the subject's life, not the fault of the biographer). This book provides a glimpse of a unique intellect whom even many of his closest associates never really felt they completely knew.

January 2015 

Feynman, Richard P. Feynman Lectures on Computation. Edited by Anthony J.G. Hey and Robin W. Allen. Reading MA: Addison-Wesley, 1996. ISBN 0-201-48991-0.

This book is derived from Feynman's lectures on the physics of computation in the mid 1980s at CalTech. A companion volume, Feynman and Computation (see September 2002), contains updated versions of presentations by guest lecturers in this course.

May 2003 

Feynman, Richard P., Fernando B. Morinigo, and William G. Wagner. Feynman Lectures on Gravitation. Edited by Brian Hatfield. Boulder, CO: Westview Press, 1995. ISBN 978-0-8133-4038-8.

In the 1962–63 academic year at Caltech, Richard Feynman taught a course on gravitation for graduate students and postdoctoral fellows. For many years the blackboard in Feynman's office contained the epigram, “What I cannot create, I do not understand.” In these lectures, Feynman discards the entire geometric edifice of Einstein's theory of gravitation (general relativity) and starts from scratch, putting himself and his students in the place of physicists from Venus (who he calls “Venutians”—Feynman was famously sloppy with spelling: he often spelled “gauge” as “guage”) who have discovered the full quantum theories of electromagnetism and the strong and weak nuclear forces but have just discovered there is a very weak attractive force between all masses, regardless of their composition. (Feynman doesn't say so, but putting on the science fiction hat one might suggest that the “Venutians” hadn't previously discovered universal gravitation because the dense clouds that shroud their planet deprived them of the ability to make astronomical observations and the lack of a moon prevented them from discovering tidal effects.)

Feynman then argues that the alien physicists would suspect that this new force worked in a manner analogous to those already known, and seek to extrapolate their knowledge of electrodynamics (the quantum theory of which Feynman had played a central part in discovering, for which he would share a Nobel prize in 1965). They would then guess that the force was mediated by particles they might dub “gravitons”. Since the force appeared to follow an inverse square law, these particles must be massless (or at least have such a small mass that deviations from the inverse square law eluded all existing experiments). Since the force was universally attractive, the spin of the graviton must be even (forces mediated by odd spin bosons such as the photon follow an attraction/repulsion rule as with static electricity; no evidence of antigravity has ever been found). Spin 0 can be ruled out because it would not couple to the spin 1 photon, which would mean gravity would not deflect light, which experiment demonstrates it does. So, we're left with a spin 2 graviton. (It might be spin 4, or 6, or higher, but there's no reason to proceed with such an assumption and the horrific complexities it entails unless we find something which rules out spin 2.)

A spin 2 graviton implies a field with a tensor potential function, and from the behaviour of gravitation we know that the tensor must be symmetric. All of this allows us, by direct analogy with electrodynamics, to write down the first draft of a field theory of gravitation which, when explored, predicts the existence of gravitational radiation, the gravitational red shift, the deflection of light by massive objects, and the precession of Mercury. Eventually Feynman demonstrates that this field theory is isomorphic to Einstein's geometrical theory, and could have been arrived at without ever invoking the concept of spacetime curvature.

In this tour de force, we get to look over the shoulder of one of the most brilliant physicists of all time as he reinvents the theory of gravitation, at a time when his goal was to produce a consistent and finite quantum theory of gravitation. Feynman's intuition was that since gravity was a far weaker force than electromagnetism, it should be easier to find a quantum theory, since the higher order terms would diminish in magnitude much more rapidly. Although Feynman's physical intuition was legendary and is much on display in these lectures, in this case it led him astray: his quest for quantum gravity failed and he soon abandoned it, and fifty years later nobody has found a suitable theory (although we've discovered a great number of things which don't work). Feynman identifies one of the key problems here—since gravitation is a universally attractive force which couples to mass-energy, and a gravitational field itself has energy, gravity gravitates, and this means that the higher order terms stretch off to infinity and can't be eliminated by clever mathematics. While these effects are negligible in laboratory experiments or on the scale of the solar system (although the first-order effect can be teased out of lunar ranging experiments), in strong field situations they blow up and the theory produces nonsense results.

These lectures were given just as the renaissance of gravitational physics was about to dawn. Discovery of extragalactic radio sources with stupendous energy output had sparked speculation about relativistic “superstars”, discussed here in chapters 13 and 14, and would soon lead to observations of quasars, which would eventually be explained by that quintessential object of general relativity, the black hole. On the theoretical side, Feynman's thesis advisor John A. Wheeler was beginning to breathe life into the long-moribund field of general relativity, and would coin the phrase “black hole” in 1967.

This book is a period piece. Some of the terminology in use at the time has become obsolete: Feynman uses “wormhole” for a black hole and “Schwarzschild singularity” for what we now call its event horizon. The discussion of “superstars” is archaic now that we understand the energy source of active galactic nuclei to be accretion onto supermassive black holes. In other areas, Feynman's insights are simply breathtaking, especially when you consider they date from half a century ago. He explores Mach's principle as the origin of inertia, cosmology and the global geometry of the universe, and gravitomagnetism.

This is not the book to read if you're interested in learning the contemporary theory of gravitation. For the most commonly used geometric approach, an excellent place to start is Misner, Thorne, and Wheeler's Gravitation. A field theory approach closer to Feynman's is presented in Weinberg's Gravitation and Cosmology. These are both highly technical works, intended for postgraduates in physics. For a popular introduction, I'd recommend Wheeler's A Journey into Gravity and Spacetime, which is now out of print, but used copies are usually available. It's only if you understand the theory, ideally at a technical level, that you can really appreciate the brilliance of Feynman's work and how prescient his insights were for the future of the field. I first read this book in 1996 and re-reading it now, having a much deeper understanding of the geometrical formulation of general relativity, I was repeatedly awestruck watching Feynman leap from insight to insight of the kind many physicists might hope to have just once in their entire careers.

Feynman gave a total of 27 lectures in the seminar. Two of the postdocs who attended, Fernando B. Morinigo and William G. Wagner, took notes for the course, from which this book is derived. Feynman corrected the notes for the first 11 lectures, which were distributed in typescript by the Caltech bookstore but never otherwise published. In 1971 Feynman approved the distribution of lectures 12–16 by the bookstore, but by then he had lost interest in gravitation and did not correct the notes. This book contains the 16 lectures Feynman approved for distribution. The remaining 11 are mostly concerned with Feynman's groping for a theory of quantum gravity. Since he ultimately failed in this effort, it's plausible to conclude he didn't believe them worthy of circulation. John Preskill and Kip S. Thorne contribute a foreword which interprets Feynman's work from the perspective of the contemporary view of gravitation.

November 2012 

Ford, Kenneth W. Building the H Bomb. Singapore: World Scientific, 2015. ISBN 978-981-4618-79-3.

In the fall of 1948, the author entered the graduate program in physics at Princeton University, hoping to obtain a Ph.D. and pursue a career in academia. In his first year, he took a course in classical mechanics taught by John Archibald Wheeler and realised that, despite the dry material of the course, he was in the presence of an extraordinary teacher and thinker, and decided he wanted Wheeler as his thesis advisor. In April of 1950, after Wheeler returned from an extended visit to Europe, the author approached him to become his advisor, not knowing in which direction his research would proceed. Wheeler immediately accepted him as a student, and then said that he (Wheeler) would be absent for a year or more at Los Alamos to work on the hydrogen bomb, and that he'd be pleased if Ford could join him on the project. Ford accepted, in large part because he believed that working on such a challenge would be “fun”, and that it would provide a chance for daily interaction with Wheeler and other senior physicists which would not exist in a regular Ph.D. program.

Well before the Manhattan project built the first fission weapon, there had been interest in fusion as an alternative source of nuclear energy. While fission releases energy by splitting heavy atoms such as uranium and plutonium into lighter atoms, fusion merges lighter atoms such as hydrogen and its isotopes deuterium and tritium into heavier nuclei like helium. While nuclear fusion can be accomplished in a desktop apparatus, doing so requires vastly more energy input than is released, making it impractical as an energy source or weapon. Still, compared to enriched uranium or plutonium, the fuel for a fusion weapon is abundant and inexpensive and, unlike a fission weapon whose yield is limited by the critical mass beyond which it would predetonate, in principle a fusion weapon could have an unlimited yield: the more fuel, the bigger the bang.

Once the Manhattan Project weaponeers became confident they could build a fission weapon, physicists, most prominent among them Edward Teller, realised that the extreme temperatures created by a nuclear detonation could be sufficient to ignite a fusion reaction in light nuclei like deuterium and that reaction, once started, might propagate by its own energy release just like the chemical fire in a burning log. It seemed plausible—the temperature of an exploding fission bomb exceeded that of the centre of the Sun, where nuclear fusion was known to occur. The big question was whether the fusion burn, once started, would continue until most of the fuel was consumed or fizzle out as its energy was radiated outward and the fuel dispersed by the explosion.

Answering this question required detailed computations of a rapidly evolving system in three dimensions with a time slice measured in nanoseconds. During the Manhattan Project, a “computer” was a woman operating a mechanical calculator, and even with large rooms filled with hundreds of “computers” the problem was intractably difficult. Unable to directly model the system, physicists resorted to analytical models which produced ambiguous results. Edward Teller remained optimistic that the design, which came to be called the “Classical Super”, would work, but many others, including J. Robert Oppenheimer, Enrico Fermi, and Stanislaw Ulam, based upon the calculations that could be done at the time, concluded it would probably fail. Oppenheimer's opposition to the Super or hydrogen bomb project has been presented as a moral opposition to development of such a weapon, but the author's contemporary recollection is that it was based upon Oppenheimer's belief that the classical super was unlikely to work, and that effort devoted to it would be at the expense of improved fission weapons which could be deployed in the near term.

All of this changed on March 9th, 1951. Edward Teller and Stanislaw Ulam published a report which presented a new approach to a fusion bomb. Unlike the classical super, which required the fusion fuel to burn on its own after being ignited, the new design, now called the Teller-Ulam design, compressed a capsule of fusion fuel by the radiation pressure of a fission detonation (usually, we don't think of radiation as having pressure, but in the extreme conditions of a nuclear explosion it far exceeds pressures we encounter with matter), and then ignited it with a “spark plug” of fission fuel at the centre of the capsule. Unlike the classical super, the fusion fuel would burn at thermodynamic equilibrium and, in doing so, liberate abundant neutrons with such a high energy they would induce fission in Uranium-238 (which cannot be fissioned by the less energetic neutrons of a fission explosion), further increasing the yield.

Oppenheimer, who had been opposed to work upon fusion, pronounced the Teller-Ulam design “technically sweet” and immediately endorsed its development. The author's interpretation is that once a design was in hand which appeared likely to work, there was no reason to believe that the Soviets who had, by that time, exploded their own fission bomb, would not also discover it and proceed to develop such a weapon, and hence it was important that the U.S. give priority to the fusion bomb to get there first. (Unlike the Soviet fission bomb, which was a copy of the U.S. implosion design based upon material obtained by espionage, there is no evidence the Soviet fusion bomb, first tested in 1955, was based upon espionage, but rather was an independent invention of the radiation implosion concept by Andrei Sakharov and Yakov Zel'dovich.)

With the Teller-Ulam design in hand, the author, working with Wheeler's group, first in Los Alamos and later at Princeton, was charged with working out the details: how precisely would the material in the bomb behave, nanosecond by nanosecond. By this time, calculations could be done by early computing machinery: first the IBM Card-Programmed Calculator and later the SEAC, which was, at the time, one of the most advanced electronic computers in the world. As with computer nerds until the present day, the author spent many nights babysitting the machine as it crunched the numbers.

On November 1st, 1952, the Ivy Mike device was detonated in the Pacific, with a yield of 10.4 megatons of TNT. John Wheeler witnessed the test from a ship at a safe distance from the island which was obliterated by the explosion. The test completely confirmed the author's computations of the behaviour of the thermonuclear burn and paved the way for deliverable thermonuclear weapons. (Ivy Mike was a physics experiment, not a weapon, but once it was known the principle was sound, it was basically a matter of engineering to design bombs which could be air-dropped.) With the success, the author concluded his work on the weapons project and returned to his dissertation, receiving his Ph.D. in 1953.

This is about half a personal memoir and half a description of the physics of thermonuclear weapons and the process by which the first weapon was designed. The technical sections are entirely accessible to readers with only a basic knowledge of physics (I was about to say “high school physics”, but I don't know how much physics, if any, contemporary high school graduates know.) There is no secret information disclosed here. All of the technical information is available in much greater detail from sources (which the author cites) such as Carey Sublette's Nuclear Weapon Archive, which is derived entirely from unclassified sources. Curiously, the U.S. Department of Energy (which has, since its inception, produced not a single erg of energy) demanded that the author heavily redact material in the manuscript, all derived from unclassified sources and dating from work done more than half a century ago. The only reason I can imagine for this is that a weapon scientist who was there, by citing information which has been in the public domain for two decades, implicitly confirms that it's correct. But it's not like the Soviets/Russians, British, French, Chinese, Israelis, and Indians haven't figured it out by themselves or that others suitably motivated can't. The author told them to stuff it, and here we have his unexpurgated memoir of the origin of the weapon which shaped the history of the world in which we live.

May 2015 

Gamow, George. One, Two, Three…Infinity. Mineola, NY: Dover, [1947] 1961. rev. ed. ISBN 0-486-25664-2.

This book, which first I read at around age twelve, rekindled my native interest in mathematics and science which had, by then, been almost entirely extinguished by six years of that intellectual torture called “classroom instruction”. Gamow was an eminent physicist: among other things, he advocated the big bang theory decades before it became fashionable, originated the concept of big bang nucleosynthesis, predicted the cosmic microwave background radiation 16 years before it was discovered, proposed the liquid drop model of the atomic nucleus, worked extensively in the astrophysics of energy production in stars, and even designed a nuclear bomb (“Greenhouse George”), which initiated the first deuterium-tritium fusion reaction here on Earth. But he was also one of most talented popularisers of science in the twentieth century, with a total of 18 popular science books published between 1939 and 1967, including the Mr Tompkins series, timeless classics which inspired many of the science visualisation projects at this site, in particular C-ship. A talented cartoonist as well, 128 of his delightful pen and ink drawings grace this volume. For a work published in 1947 with relatively minor revisions in the 1961 edition, this book has withstood the test of time remarkably well—Gamow was both wise and lucky in his choice of topics. Certainly, nobody should consider this book a survey of present-day science, but for folks well-grounded in contemporary orthodoxy, it's a delightful period piece providing a glimpse of the scientific world view of almost a half-century ago as explained by a master of the art. This Dover paperback is an unabridged reprint of the 1961 revised edition.

September 2004 

Gleick, James. Isaac Newton. New York: Pantheon Books, 2003. ISBN 0-375-42233-1.

Fitting a satisfying biography of one of the most towering figures in the history of the human intellect into fewer than 200 pages is a formidable undertaking, which James Gleick has accomplished magnificently here. Newton's mathematics and science are well covered, placing each in the context of the “shoulders of Giants” which he said helped him see further, but also his extensive (and little known, prior to the twentieth century) investigations into alchemy, theology, and ancient history. His battles with Hooke, Leibniz, and Flamsteed, autocratic later years as Master of the Royal Mint and President of the Royal Society and ceaseless curiosity and investigation are well covered, as well as his eccentricity and secretiveness. I'm a little dubious of the discussion on pp. 186–187 where Newton is argued to have anticipated or at least left the door open for relativity, quantum theory, equivalence of mass and energy, and subatomic forces. Newton wrote millions of words on almost every topic imaginable, most for his own use with no intention of publication, few examined by scholars until centuries after his death. From such a body of text, it may be possible to find sentences here and there which “anticipate” almost anything when you know from hindsight what you're looking for. In any case, the achievements of Newton, who not only laid the foundation of modern physical science, invented the mathematics upon which much of it is based, and created the very way we think about and do science, need no embellishment. The text is accompanied by 48 pages of endnotes (the majority citing primary sources) and an 18 page bibliography. A paperback edition is now available.

November 2004 

Gleick, James. Time Travel. New York: Pantheon Books, 2016. ISBN 978-0-307-90879-7.

In 1895, a young struggling writer who earned his precarious living by writing short humorous pieces for London magazines, often published without a byline, buckled down and penned his first long work, a longish novella of some 33,000 words. When published, H. G. Wells's The Time Machine would not only help to found a new literary genre—science fiction, but would introduce a entirely new concept to storytelling: time travel. Many of the themes of modern fiction can be traced to the myths of antiquity, but here was something entirely new: imagining a voyage to the future to see how current trends would develop, or back into the past, perhaps not just to observe history unfold and resolve its persistent mysteries, but possibly to change the past, opening the door to paradoxes which have been the subject not only of a multitude of subsequent stories but theories and speculation by serious scientists. So new was the concept of travel through time that the phrase “time travel” first appeared in the English language only in 1914, in a reference to Wells's story.

For much of human history, there was little concept of a linear progression of time. People lived lives much the same as those of their ancestors, and expected their descendants to inhabit much the same kind of world. Their lives seemed to be governed by a series of cycles: day and night, the phases of the Moon, the seasons, planting and harvesting, and successive generations of humans, rather than the ticking of an inexorable clock. Even great disruptive events such as wars, plagues, and natural disasters seemed to recur over time, even if not on a regular, predictable schedule. This led to the philosophical view of “eternal return”, which appears in many ancient cultures and in Western philosophy from Pythagoras to Neitzsche. In mathematics, the Poincaré recurrence theorem formally demonstrated that an isolated finite system will eventually (although possibly only after a time much longer than the age of the universe), return to a given state and repeat its evolution an infinite number of times.

But nobody (except perhaps a philosopher) who had lived through the 19th century in Britain could really believe that. Over the space of a human lifetime, the world and the human condition had changed radically and seemed to be careening into a future difficult to envision. Steam power, railroads, industrialisation of manufacturing, the telegraph and telephone, electricity and the electric light, anaesthesia, antiseptics, steamships and global commerce, submarine cables and near-instantaneous international communications, had all remade the world. The idea of progress was not just an abstract concept of the Enlightenment, but something anybody could see all around them.

But progress through what? In the fin de siècle milieu that Wells inhabited, through time: a scroll of history being written continually by new ideas, inventions, creative works, and the social changes flowing from these events which changed the future in profound and often unknowable ways. The intellectual landscape was fertile for utopian ideas, many of which Wells championed. Among the intellectual élite, the fourth dimension was much in vogue, often a fourth spatial dimension but also the concept of time as a dimension comparable to those of space. This concept first appears in the work of Edgar Allan Poe in 1848, but was fully fleshed out by Wells in The Time Machine: “ ‘Clearly,’ the Time Traveller proceeded, ‘any real body must have extension in four dimensions: it must have Length, Breadth, Thickness, and—Duration.’ ” But if we can move freely through the three spatial directions (although less so in the vertical in Wells's day than the present), why cannot we also move back and forth in time, unshackling our consciousness and will from the tyranny of the timepiece just as the railroad, steamship, and telegraph had loosened the constraints of locality?

Just ten years after The Time Machine, Einstein's special theory of relativity resolved puzzles in electrodynamics and mechanics by demonstrating that time and space mixed depending upon the relative states of motion of observers. In 1908, Hermann Minkowski reformulated Einstein's theory in terms of a four dimensional space-time. He declared, “Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.” (Einstein was, initially, less than impressed with this view, calling it “überflüssige Gelehrsamkeit”: superfluous learnedness, but eventually accepted the perspective and made it central to his 1915 theory of gravitation.) But further, embedded within special relativity, was time travel—at least into the future.

According to the equations of special relativity, which have been experimentally verified as precisely as anything in science and are fundamental to the operation of everyday technologies such as the Global Positioning System, a moving observer will measure time to flow more slowly than a stationary observer. We don't observe this effect in everyday life because the phenomenon only becomes pronounced at velocities which are a substantial fraction of the speed of light, but even at the modest velocity of orbiting satellites, it cannot be neglected. Due to this effect of time dilation, if you had a space ship able to accelerate at a constant rate of one Earth gravity (people on board would experience the same gravity as they do while standing on the Earth's surface), you would be able to travel from the Earth to the Andromeda galaxy and back to Earth, a distance of around four million light years, in a time, measured by the ship's clock and your own subjective and biological perception of time, in less than six and a half years. But when you arrived back at the Earth, you'd discover that in its reference frame, more than four million years of time would have elapsed. What wonders would our descendants have accomplished in that distant future, or would they be digging for grubs with blunt sticks while living in a sustainable utopia having finally thrown off the shackles of race, class, and gender which make our present civilisation a living Hell?

This is genuine time travel into the future and, although it's far beyond our present technological capabilities, it violates no law of physics and, to a more modest yet still measurable degree, happens every time you travel in an automobile or airplane. But what about travel into the past? Travel into the future doesn't pose any potential paradoxes. It's entirely equivalent to going into hibernation and awaking after a long sleep—indeed, this is a frequently-used literary device in fiction depicting the future. Travel into the past is another thing entirely. For example, consider the grandfather paradox: suppose you have a time machine able to transport you into the past. You go back in time and kill your own grandfather (it's never the grandmother—beats me). Then who are you, and how did you come into existence in the first place? The grandfather paradox exists whenever altering an event in the past changes conditions in the future so as to be inconsistent with the alteration of that event.

Or consider the bootstrap paradox or causal loop. An elderly mathematician (say, age 39), having struggled for years and finally succeeded in proving a difficult theorem, travels back in time and provides a key hint to his twenty year old self to set him on the path to the proof—the same hint he remembers finding on his desk that morning so many years before. Where did the idea come from? In 1991, physicist David Deutsch demonstrated that a computer incorporating travel back in time (formally, a closed timelike curve) could solve NP problems in polynomial time. I wonder where he got that idea….

All of this would be academic were time travel into the past just a figment of fictioneers' imagination. This has been the view of many scientists, and the chronology protection conjecture asserts that the laws of physics conspire to prevent travel to the past which, in the words of a 1992 paper by Stephen Hawking, “makes the universe safe for historians.” But the laws of physics, as we understand them today, do not rule out travel into the past! Einstein's 1915 general theory of relativity, which so far has withstood every experimental test for over a century, admits solutions, such as the Gödel metric, discovered in 1949 by Einstein's friend and colleague Kurt Gödel, which contain closed timelike curves. In the Gödel universe, which consists of a homogeneous sea of dust particles, rotating around a centre point and with a nonzero cosmological constant, it is possible, by travelling on a closed path and never reaching or exceeding the speed of light, to return to a point in one's own past. Now, the Gödel solution is highly contrived, and there is no evidence that it describes the universe we actually inhabit, but the existence of such a solution leaves the door open that somewhere in the other exotica of general relativity such as spinning black holes, wormholes, naked singularities, or cosmic strings, there may be a loophole which allows travel into the past. If you discover one, could you please pop back and send me an E-mail about it before I finish this review?

This book is far more about the literary and cultural history of time travel than scientific explorations of its possibility and consequences. Thinking about time travel forces one to confront questions which can usually be swept under the rug: is the future ours to change, or do we inhabit a block universe where our perception of time is just a delusion as the cursor of our consciousness sweeps out a path in a space-time whose future is entirely determined by its past? If we have free will, where does it come from, when according to the laws of physics the future can be computed entirely from the past? If we can change the future, why not the past? If we changed the past, would it change the present for those living in it, or create a fork in the time line along which a different history would develop? All of these speculations are rich veins to be mined in literature and drama, and are explored here. Many technical topics are discussed only briefly, if at all, for example the Wheeler-Feynman absorber theory, which resolves a mystery in electrodynamics by positing a symmetrical solution to Maxwell's equations in which the future influences the past just as the present influences the future. Gleick doesn't go anywhere near my own experiments with retrocausality or the “presponse” experiments of investigators such as Dick Bierman and Dean Radin. I get it—pop culture beats woo-woo on the bestseller list.

The question of time has puzzled people for millennia. Only recently have we thought seriously about travel in time and its implications for our place in the universe. Time travel has been, and will doubtless continue to be the source of speculation and entertainment, and this book is an excellent survey of its short history as a genre of fiction and the science upon which it is founded.

August 2017 

Goldsmith, Barbara. Obsessive Genius. New York: W. W. Norton, 2005. ISBN 978-0-393-32748-9.

Maria Salomea Skłodowska was born in 1867 in Warsaw, Poland, then part of the Russian Empire. She was the fifth and last child born to her parents, Władysław and Bronisława Skłodowski, both teachers. Both parents were members of a lower class of the aristocracy called the Szlachta, but had lost their wealth through involvement in the Polish nationalist movement opposed to Russian rule. They retained the love of learning characteristic of their class, and had independently obtained teaching appointments before meeting and marrying. Their children were raised in an intellectual atmosphere, with their father reading books aloud to them in Polish, Russian, French, German, and English, all languages in which he was fluent.

During Maria's childhood, her father lost his teaching position after his anti-Russian sentiments and activities were discovered, and supported himself by operating a boarding school for boys from the provinces. In cramped and less than sanitary conditions, one of the boarders infected two of the children with typhus: Marie's sister Zofia died. Three years later, her mother, Bronisława, died of tuberculosis. Maria experienced her first episode of depression, a malady which would haunt her throughout life.

Despite having graduated from secondary school with honours, Marie and her sister Bronisława could not pursue their education in Poland, as the universities did not admit women. Marie made an agreement with her older sister: she would support Bronisława's medical education at the Sorbonne in Paris in return for her supporting Maria's studies there after she graduated and entered practice. Maria worked as a governess, supporting Bronisława. Finally, in 1891, she was able to travel to Paris and enroll in the Sorbonne. On the registration forms, she signed her name as “Marie”.

One of just 23 women among the two thousand enrolled in the School of Sciences, Marie studied physics, chemistry, and mathematics under an eminent faculty including luminaries such as Henri Poincaré. In 1893, she earned her degree in physics, one of only two women to graduate with a science degree that year, and in 1894 obtained a second degree in mathematics, ranking second in her class.

Finances remained tight, and Marie was delighted when one of her professors, Gabriel Lippman, arranged for her to receive a grant to study the magnetic properties of different kinds of steel. She set to work on the project but made little progress because the equipment she was using in Lippman's laboratory was cumbersome and insensitive. A friend recommended she contact a little-known physicist who was an expert on magnetism in metals and had developed instruments for precision measurements. Marie arranged to meet Pierre Curie to discuss her work.

Pierre was working at the School of Industrial Physics and Chemistry of the City of Paris (EPCI), an institution much less prestigious than the Sorbonne, in a laboratory which the visiting Lord Kelvin described as “a cubbyhole between the hallway and a student laboratory”. Still, he had major achievements to his credit. In 1880, with his brother Jacques, he had discovered the phenomenon of piezoelectricity, the interaction between electricity and mechanical stress in solids. Now the foundation of many technologies, the Curies used piezoelectricity to build an electrometer much more sensitive than previous instruments. His doctoral dissertation on the effects of temperature on the magnetism of metals introduced the concept of a critical temperature, different for each metal or alloy, at which permanent magnetism is lost. This is now called the Curie temperature.

When Pierre and Marie first met, they were immediately taken with one another: both from families of modest means, largely self-educated, and fascinated by scientific investigation. Pierre rapidly fell in love and was determined to marry Marie, but she, having been rejected in an earlier relationship in Poland, was hesitant and still planned to return to Warsaw. Pierre eventually persuaded Marie, and the two were married in July 1895. Marie was given a small laboratory space in the EPCI building to pursue work on magnetism, and henceforth the Curies would be a scientific team.

In the final years of the nineteenth century “rays” were all the rage. In 1896, Wilhelm Conrad Röntgen discovered penetrating radiation produced by accelerating electrons (which he called “cathode rays”, as the electron would not be discovered until the following year) into a metal target. He called them “X-rays”, using “X” as the symbol for the unknown. The same year, Henri Becquerel discovered that a sample of uranium salts could expose a photographic plate even if the plate were wrapped in a black cloth. In 1897 he published six papers on these “Becquerel rays”. Both discoveries were completely accidental.

The year that Marie was ready to begin her doctoral research, 65 percent of the papers presented at the Academy of Sciences in Paris were devoted to X-rays. Pierre suggested that Marie investigate the Becquerel rays produced by uranium, as they had been largely neglected by other scientists. She began a series of experiments using an electrometer designed by Pierre. The instrument was sensitive but exasperating to operate: Lord Rayleigh later wrote that electrometers were “designed by the devil”. Patiently, Marie measured the rays produced by uranium and then moved on to test samples of other elements. Among them, only thorium produced detectable rays.

She then made a puzzling observation. Uranium was produced from an ore called pitchblende. When she tested a sample of the residue of pitchblende from which all of the uranium had been extracted, she measured rays four times as energetic as those from pure uranium. She inferred that there must be a substance, perhaps a new chemical element, remaining in the pitchblende residue which was more radioactive than uranium. She then tested a thorium ore and found it also to produce rays more energetic than pure thorium. Perhaps here was yet another element to be discovered.

In March 1898, Marie wrote a paper in which she presented her measurements of the uranium and thorium ores, introduced the word “radioactivity” to describe the phenomenon, put forth the hypothesis that one or more undiscovered elements were responsible, suggested that radioactivity could be used to discover new elements, and, based upon her observations that radioactivity was unaffected by chemical processes, that it must be “an atomic property”. Neither Pierre nor Marie were members of the Academy of Sciences; Marie's former professor, Gabriel Lippman, presented the paper on her behalf.

It was one thing to hypothesise the existence of a new element or elements, and entirely another to isolate the element and determine its properties. Ore, like pitchblende, is a mix of chemical compounds. Starting with ore from which the uranium had been extracted, the Curies undertook a process to chemically separate these components. Those found to be radioactive were then distilled to increase their purity. With each distillation their activity increased. They finally found two of these fractions contained all the radioactivity. One was chemically similar to barium, while the other resembled bismuth. Measuring the properties of the fractions indicated they must be a mixture of the new radioactive elements and other, lighter elements.

To isolate the new elements, a process called “fractionation” was undertaken. When crystals form from a solution, the lighter elements tend to crystallise first. By repeating this process, the heavier elements could slowly be concentrated. With each fractionation the radioactivity increased. Working with the fraction which behaved like bismuth, the Curies eventually purified it to be 400 times as radioactive as uranium. No spectrum of the new element could yet be determined, but the Curies were sufficiently confident in the presence of a new element to publish a paper in July 1898 announcing the discovery and naming the new element “polonium” after Marie's native Poland. In December, working with the fraction which chemically resembled barium, they produced a sample 900 times as radioactive as uranium. This time a clear novel spectral line was found, and at the end of December 1898 they announced the discovery of a second new element, which they named “radium”.

Two new elements had been discovered, with evidence sufficiently persuasive that their existence was generally accepted. But the existing samples were known to be impure. The physical and chemical properties of the new elements, allowing their places in the periodic table to be determined, would require removal of the impurities and isolation of pure samples. The same process of fractionation could be used, but since it quickly became clear that the new radioactive elements were a tiny fraction of the samples in which they had been discovered, it would be necessary to scale up the process to something closer to an industrial scale. (The sample in which radium had been identified was 900 times more radioactive than uranium. Pure radium was eventually found to be ten million times as radioactive as uranium.)

Pierre learned that the residue from extracting uranium from pitchblende was dumped in a forest near the uranium mine. He arranged to have the Austrian government donate the material at no cost, and found the funds to ship it to the laboratory in Paris. Now, instead of test tubes, they were working with tons of material. Pierre convinced a chemical company to perform the first round of purification, persuading them that other researchers would be eager to buy the resulting material. Eventually, they delivered twenty kilogram lots of material to the Curies which were fifty times as radioactive as uranium. From there the Curie laboratory took over the subsequent purification. After four years, processing ten tons of pitchblende residue, hundreds of tons of rinsing water, thousands of fractionations, one tenth of a gram of radium chloride was produced that was sufficiently pure to measure its properties. In July 1902 Marie announced the isolation of radium and placed it on the periodic table as element 88.

In June of 1903, Marie defended her doctoral thesis, becoming the first woman in France to obtain a doctorate in science. With the discovery of radium, the source of the enormous energy it and other radioactive elements released became a major focus of research. Ernest Rutherford argued that radioactivity was a process of “atomic disintegration” in which one element was spontaneously transmuting to another. The Curies originally doubted this hypothesis, but after repeating the experiments of Rutherford, accepted his conclusion as correct.

In 1903, the Nobel Prize for Physics was shared by Marie and Pierre Curie and Henri Becquerel, awarded for the discovery of radioactivity. The discovery of radium and polonium was not mentioned. Marie embarked on the isolation of polonium, and within two years produced a sample sufficiently pure to place it as element 84 on the periodic table with an estimate of its half-life of 140 days (the modern value is 138.4 days). Polonium is about 5000 times as radioactive as radium. Polonium and radium found in nature are the products of decay of primordial uranium and thorium. Their half-lives are so short (radium's is 1600 years) that any present at the Earth's formation has long since decayed.

After the announcement of the discovery of radium and the Nobel prize, the Curies, and especially Marie, became celebrities. Awards, honorary doctorates, and memberships in the academies of science of several countries followed, along with financial support and the laboratory facilities they had lacked while performing the work which won them such acclaim. Radium became a popular fad, hailed as a cure for cancer and other diseases, a fountain of youth, and promoted by quacks promising all kinds of benefits from the nostrums they peddled, some of which, to the detriment of their customers, actually contained minute quantities of radium.

Tragedy struck in April 1906 when Pierre was killed in a traffic accident: run over on a Paris street in a heavy rainstorm by a wagon pulled by two horses. Marie was inconsolable, immersing herself in laboratory work and neglecting her two young daughters. Her spells of depression returned. She continued to explore the properties of radium and polonium and worked to establish a standard unit to measure radioactive decay, calibrated by radium. (This unit is now called the curie, but is no longer defined based upon radium and has been replaced by the becquerel, which is simply an inverse second.) Marie Curie was not interested or involved in the work to determine the structure of the atom and its nucleus or the development of quantum theory. The Curie laboratory continued to grow, but focused on production of radium and its applications in medicine and industry. Lise Meitner applied for a job at the laboratory and was rejected. Meitner later said she believed that Marie thought her a potential rival to Curie's daughter Irène. Meitner joined the Kaiser Wilhelm Institute in Berlin and went on to co-discover nuclear fission. The only two chemical elements named in whole or part for women are curium (element 96, named for both Pierre and Marie) and meitnerium (element 109).

In 1910, after three years of work with André-Louis Debierne, Marie managed to produce a sample of metallic radium, allowing a definitive measurement of its properties. In 1911, she won a second Nobel prize, unshared, in chemistry, for the isolation of radium and polonium. At the moment of triumph, news broke of a messy affair she had been carrying on with Pierre's successor at the EPCI, Paul Langevin, a married man. The popular press, who had hailed Marie as a towering figure of French science, went after her with bared fangs and mockery, and she went into seclusion under an assumed name.

During World War I, she invented and promoted the use of mobile field X-ray units (called “Les Petites Curies”) and won acceptance for women to operate them near the front, with her daughter Irène assisting in the effort. After the war, her reputation largely rehabilitated, Marie not only accepted but contributed to the growth of the Curie myth, seeing it as a way to fund her laboratory and research. Irène took the lead at the laboratory.

As co-discoverer of the phenomenon of radioactivity and two chemical elements, Curie's achievements were well recognised. She was the first woman to win a Nobel prize, the first person to win two Nobel prizes, and the only person so far to win Nobel prizes in two different sciences. (The third woman to win a Nobel prize was her daughter, Irène Joliot-Curie, for the discovery of artificial radioactivity.) She was the first woman to be appointed a full professor at the Sorbonne.

Marie Curie died of anæmia in 1934, probably brought on by exposure to radiation over her career. She took few precautions, and her papers and personal effects remain radioactive to this day. Her legacy is one of dedication and indefatigable persistence in achieving the goals she set for herself, regardless of the scientific and technical challenges and the barriers women faced at the time. She demonstrated that pure persistence, coupled with a brilliant intellect, can overcome formidable obstacles.

April 2016 

Goldsmith, Donald. The Runaway Universe. New York: Perseus Books, 2000. ISBN 0-7382-0068-9.

January 2001 

Gott, J. Richard III. Time Travel in Einstein's Universe. New York: Houghton Mifflin, 2001. ISBN 0-395-95563-7.

May 2001 

Greenberg, Stanley. Time Machines. Munich: Hirmer Verlag, 2011. ISBN 978-3-7774-4041-5.

Should our civilisation collapse due to folly, shortsightedness, and greed, and an extended dark age ensue, in which not only our painfully-acquired knowledge is lost, but even the memory of what we once knew and accomplished forgotten, certainly among the most impressive of the achievements of our lost age when discovered by those who rise from the ruins to try again will be the massive yet delicate apparatus of our great physics experiments. Many, buried deep in the Earth, will survive the chaos of the dark age and beckon to pioneers of the next age of discovery just as the tombs of Egypt did to those in our epoch. Certainly, when the explorers of that distant time first illuminate the great detector halls of our experiments, they will answer, as Howard Carter did when asked by Lord Carnarvon, “Can you see anything?”, “Yes, wonderful things.”

This book is a collection of photographs of these wonderful things, made by a master photographer and printed in a large-format (26×28 cm) coffee-table book. We visit particle accelerators in Japan, the United States, Canada, Switzerland, Italy, and Germany; gravitational wave detectors in the U.S. and Italy; neutrino detectors in Canada, Japan, the U.S., Italy, and the South Pole; and the 3000 km² cosmic ray observatory in Argentina.

This book is mostly about the photographs, not the physics or engineering: the photographs are masterpieces. All are reproduced in monochrome, which emphasises the beautiful symmetries of these machines without the distractions of candy-coloured cable bundles. There is an introduction by particle physicist David C. Cassidy which briefly sketches the motivation for building these cathedrals of science and end notes which provide additional details of the hardware in each photograph, but you don't pay the substantial price of the book for these. The photographs are obviously large format originals (nobody could achieve this kind of control of focus and tonal range with a convenient to use camera) and they are printed exquisitely. The screen is so fine I have difficulty evaluating it even with a high power magnifier, but it looks to me like the book was printed using not just a simple halftone screen but with ink in multiple shades of grey.

The result is just gorgeous. Resist the temptation to casually flip from image to image—immerse yourself in each of them and work out the perspective. One challenge is that it's often difficult to determine the scale of what you're looking at from a cursory glance at the picture. You have to search for something with which you're familiar until it all snaps into scale; this is sometimes difficult and I found the disorientation delightful and ultimately enlightening.

You will learn nothing about physics from this book. You will learn nothing about photography apart from a goal to which to aspire as you master the art. But you will see some of the most amazing creations of the human mind, built in search of the foundations of our understanding of the universe we inhabit, photographed by a master and reproduced superbly, inviting you to linger on every image and wish you could see these wonders with your own eyes.

December 2012 

Haisch, Bernard. The God Theory. San Francisco: Weiser, 2006. ISBN 1-57863-374-5.

This is one curious book. Based on acquaintance with the author and knowledge of his work, including the landmark paper “Inertia as a zero-point-field Lorentz force” (B. Haisch, A. Rueda & H.E. Puthoff, Physical Review A, Vol. 49, No. 2, pp. 678–694 [1994]), I expected this to be a book about the zero-point field and its potential to provide a limitless source of energy and Doc Smith style inertialess propulsion. The title seemed odd, but there's plenty of evidence that when it comes to popular physics books, “God sells”.

But in this case the title could not be more accurate—this book really is a God Theory—that our universe was created, in the sense of its laws of physics being defined and instantiated, then allowed to run their course, by a being with infinite potential who did so in order to experience, in the sum of the consciousness of its inhabitants, the consequences of the creation. (Defining the laws isn't the same as experiencing their playing out, just as writing down the rules of chess isn't equivalent to playing all possible games.) The reason the constants of nature appear to be fine-tuned for the existence of consciousness is that there's no point in creating a universe in which there will be no observers through which to experience it, and the reason the universe is comprehensible to us is that our consciousness is, in part, one with the being who defined them. While any suggestion of this kind is enough to get what Haisch calls adherents of “fundamentalist scientism” sputtering if not foaming at the mouth, he quite reasonably observes that these self-same dogmatic reductionists seem perfectly willing to admit an infinite number of forever unobservable parallel universes created purely at random, and to inhabit a universe which splits into undetectable multiple histories with every quantum event, rather than contemplate that the universe might have a purpose or that consciousness may play a rôle in physical phenomena.

The argument presented here is reminiscent in content, albeit entirely different in style, to that of Scott Adams's God's Debris (February 2002), a book which is often taken insufficiently seriously because its author is the creator of Dilbert. Of course, there is another possibility about which I have written again, again, again, and again, which is that our universe was not created ex nihilo by an omnipotent being outside of space and time, but is rather a simulation created by somebody with a computer whose power we can already envision, run not to experience the reality within, but just to see what happens. Or, in other words, “it isn't a universe, it's a science fair project!” In The God Theory, your consciousness is immortal because at death your experience rejoins the One which created you. In the simulation view, you live on forever on a backup tape. What's the difference?

Seriously, this is a challenging and thought-provoking argument by a distinguished scientist who has thought deeply on these matters and is willing to take the professional risk of talking about them to the general public. There is much to think about here, and integrating it with other outlooks on these deep questions will take far more time than it takes to read this book.

May 2007 

Haisch, Bernard. The Purpose-Guided Universe. Franklin Lakes, NJ: Career Press, 2010. ISBN 978-1-60163-122-0.

The author, an astrophysicist who was an editor of the Astrophysical Journal for a decade, subtitles this book “Believing In Einstein, Darwin, and God”. He argues that the militant atheists who have recently argued that science is incompatible with belief in a Creator are mistaken and that, to the contrary, recent scientific results are not only compatible with, but evidence for, the intelligent design of the laws of physics and the initial conditions of the universe.

Central to his argument are the variety of “fine tunings” of the physical constants of nature. He lists ten of these in the book's summary, but these are chosen from a longer list. These are quantities, such as the relative masses of the neutron and proton, the ratio of the strength of the electromagnetic and gravitational forces, and the curvature of spacetime immediately after the Big Bang which, if they differed only slightly from their actual values, would have resulted in a universe in which the complexity required to evolve any imaginable form of life would not exist. But, self evidently, we're here, so we have a mystery to explain. There are really only three possibilities:

1. The values of the fine-tuned parameters are those we measure because they can't be anything else. One day we'll discover a master equation which allows us to predict their values from first principles, and we'll discover that any change to that equation produces inconsistent results. The universe is fine tuned because that's the only way it could be.
2. The various parameters were deliberately fine tuned by an intelligent, conscious designer bent on creating a universe in which sufficient complexity could evolve so as to populate it with autonomous, conscious beings. The universe is fine tuned by a creator because that's necessary to achieve the goal of its creation.
3. The parameters are random, and vary from universe to universe among an ensemble in a “multiverse” encompassing a huge, and possibly infinite number of universes with no causal connection to one another. We necessarily find the parameters of the universe we inhabit to be fine tuned to permit ourselves to exist because if they weren't, we wouldn't be here to make the observations and puzzle over the results. The universe is fine tuned because it's just one of a multitude with different settings, and we can only observe one which happens to be tuned for us.

For most of the history of science, it was assumed that possibility (1)—inevitability by physical necessity—was what we'd ultimately discover once we'd teased out the fundamental laws at the deepest level of nature. Unfortunately, despite vast investment in physics, both experimental and theoretical, astronomy, and cosmology, which has matured in the last two decades from wooly speculation to a precision science, we have made essentially zero progress toward this goal. String theory, which many believed in the heady days of the mid-1980s to be the path to that set of equations you could wear on a T-shirt and which would crank out all the dial settings of our universe, now seems to indicate to some (but not all) of those pursuing it, that possibility (3): a vast “landscape” of universes, all unobservable even in principle, one of which with wildly improbable properties we find ourselves in because we couldn't exist in most of the others is the best explanation.

Maybe, the author argues, we should take another look at possibility (2). Orthodox secular scientists are aghast at the idea, arguing that to do so is to “abandon science” and reject rational inference from experimental results in favour of revelation based only on faith. Well, let's compare alternatives (2) and (3) in that respect. Number three asks us to believe in a vast or infinite number of universes, all existing in their own disconnected bubbles of spacetime and unable to communicate with one another, which cannot be detected by any imaginable experiment, without any evidence for the method by which they were created nor idea how it all got started. And all of this to explain the laws and initial conditions of the single universe we inhabit. How's that for taking things on faith?

The author's concept of God in this volume is not that of the personal God of the Abrahamic religions, but rather something akin to the universal God of some Eastern religions, as summed up in Aldous Huxley's The Perennial Philosophy. This God is a consciousness encompassing the entire universe which causes the creation of its contents, deliberately setting things up to maximise the creation of complexity, with the eventual goal of creating more and more consciousness through which the Creator can experience the universe. This is actually not unlike the scenario sketched in Scott Adams's God's Debris, which people might take with the seriousness it deserves had it been written by somebody other than the creator of Dilbert.

If you're a regular reader of this chronicle, you'll know that my own personal view is in almost 100% agreement with Dr. Haisch on the big picture, but entirely different on the nature of the Creator. I'll spare you the detailed exposition, as you can read it in my comments on Sean Carroll's From Eternity to Here (February 2010). In short, I think it's more probable than not we're living in a simulation, perhaps created by a thirteen year old post-singularity superkid as a science fair project. Unlike an all-pervading but imperceptible Brahman or an infinitude of unobservable universes in an inaccessible multiverse, the simulation hypothesis makes predictions which render it falsifiable, and hence a scientific theory. Eventually, precision measurements will discover, then quantify, discrepancies due to round-off errors in the simulation (for example, an integration step which is too large), and—what do you know—we already have in hand a collection of nagging little discrepancies which look doggone suspicious to me.

This is not one of those mushy “science and religion can coexist” books. It is an exploration, by a serious scientist who has thought deeply about these matters, of why evidence derived entirely from science is pointing those with minds sufficiently open to entertain the idea, that the possibility of our universe having been deliberately created by a conscious intelligence who endowed it with the properties that permit it to produce its own expanding consciousness is no more absurd that the hypotheses favoured by those who reject that explanation, and is entirely compatible with recent experimental results, which are difficult in the extreme to explain in any other manner. Once the universe is created (or, as I'd put it, the simulation is started), there's no reason for the Creator to intervene: if all the dials and knobs are set correctly, the laws discovered by Einstein, Darwin, Maxwell, and others will take care of the rest. Hence there's no conflict between science and evidence-based belief in a God which is the first cause for all which has happened since.

October 2010 

Hawking, Stephen. The Universe in a Nutshell. New York: Bantam Books, 2001. ISBN 0-553-80202-X.

January 2002 

Herken. Gregg. Brotherhood of the Bomb. New York: Henry Holt, 2002. ISBN 0-8050-6589-X.

What more's to be said about the tangled threads of science, politics, ego, power, and history that bound together the lives of Ernest O. Lawrence, J. Robert Oppenheimer, and Edward Teller from the origin of the Manhattan Project through the postwar controversies over nuclear policy and the development of thermonuclear weapons? In fact, a great deal, as declassification of FBI files, including wiretap transcripts, release of decrypted Venona intercepts of Soviet espionage cable traffic, and documents from Moscow archives opened to researchers since the collapse of the Soviet Union have provide a wealth of original source material illuminating previously dark corners of the epoch.

Gregg Herken, a senior historian and curator at the National Air and Space Museum, draws upon these resources to explore the accomplishments, conflicts, and controversies surrounding Lawrence, Oppenheimer, and Teller, and the cold war era they played such a large part in defining. The focus is almost entirely on the period in which the three were active in weapons development and policy—there is little discussion of their prior scientific work, nor of Teller's subsequent decades on the public stage. This is a serious academic history, with almost 100 pages of source citations and bibliography, but the story is presented in an engaging manner which leaves the reader with a sense of the personalities involved, not just their views and actions. The author writes with no discernible ideological bias, and I noted only one insignificant technical goof.

May 2005 

Hey, Anthony J.G. ed. Feynman and Computation. Boulder, CO: Westview Press, 2002. ISBN 0-8133-4039-X.

September 2002 

Hirshfeld, Alan. The Electric Life of Michael Faraday. New York: Walker and Company, 2006. ISBN 978-0-8027-1470-1.

Of post-Enlightenment societies, one of the most rigidly structured by class and tradition was that of Great Britain. Those aspiring to the life of the mind were overwhelmingly the well-born, educated in the classics at Oxford or Cambridge, with the wealth and leisure to pursue their interests on their own. The career of Michael Faraday stands as a monument to what can be accomplished, even in such a stultifying system, by the pure power of intellect, dogged persistence, relentless rationality, humility, endless fascination with the intricacies of creation, and confidence that it was ultimately knowable through clever investigation.

Faraday was born in 1791, the third child of a blacksmith who had migrated to London earlier that year in search of better prospects, which he never found due to fragile health. In his childhood, Faraday's family occasionally got along only thanks to the charity of members of the fundamentalist church to which they belonged. At age 14, Faraday was apprenticed to a French émigré bookbinder, setting himself on the path to a tradesman's career. But Faraday, while almost entirely unschooled, knew how to read, and read he did—as many of the books which passed through the binder's shop as he could manage. As with many who read widely, Faraday eventually came across a book that changed his life, The Improvement of the Mind by Isaac Watts, and from the pragmatic and inspirational advice in that volume, along with the experimental approach to science he learned from Jane Marcet's Conversations in Chemistry, Faraday developed his own philosophy of scientific investigation and began to do his own experiments with humble apparatus in the bookbinder's shop.

Faraday seemed to be on a trajectory which would frustrate his curiosity forever amongst the hammers, glue, and stitches of bookbindery when, thanks to his assiduous note-taking at science lectures, his employer passing on his notes, and a providential vacancy, he found himself hired as the assistant to the eminent Humphry Davy at the Royal Institution in London. Learning chemistry and the emerging field of electrochemistry at the side of the master, he developed the empirical experimental approach which would inform all of his subsequent work.

Faraday originally existed very much in Davy's shadow, even serving as his personal valet as well as scientific assistant on an extended tour of the Continent, but slowly (and over Davy's opposition) rose to become a Fellow of the Royal Institution and director of its laboratory. Seeking to shore up the shaky finances of the Institution, in 1827 he launched the Friday Evening Discourses, public lectures on a multitude of scientific topics by Faraday and other eminent scientists, which he would continue to supervise until 1862.

Although trained as a chemist, and having made his reputation in that field, his electrochemical investigations with Davy had planted in his mind the idea that electricity was not a curious phenomenon demonstrated in public lectures involving mysterious “fluids”, but an essential component in understanding the behaviour of matter. In 1831, he turned his methodical experimental attention to the relationship between electricity and magnetism, and within months had discovered electromagnetic induction: that an electric current was induced in a conductor only by a changing magnetic field: the principle used by every electrical generator and transformer in use today. He built the first dynamo, using a spinning copper disc between the poles of a strong magnet, and thereby demonstrated the conversion of mechanical energy into electricity for the first time. Faraday's methodical, indefatigable investigations, failures along with successes, were chronicled in a series of papers eventually collected into the volume Experimental Researches in Electricity, which is considered to be one of the best narratives ever written of science as it is done.

Knowing little mathematics, Faraday expressed the concepts he discovered in elegant prose. His philosophy of science presaged that of Karl Popper and the positivists of the next century—he considered all theories as tentative, advocated continued testing of existing theories in an effort to falsify them and thereby discover new science beyond them, and he had no use whatsoever for the unobservable: he detested concepts such as “action at a distance”, which he considered mystical obfuscation. If some action occurred, there must be some physical mechanism which causes it, and this led him to formulate what we would now call field theory: that physical lines of force extend from electrically charged objects and magnets through apparently empty space, and it is the interaction of objects with these lines of force which produces the various effects he had investigated. This flew in the face of the scientific consensus of the time, and while universally admired for his experimental prowess, many regarded Faraday's wordy arguments as verging on the work of a crank. It wasn't until 1857 that the ageing Faraday made the acquaintance of the young James Clerk Maxwell, who had sent him a copy of a paper in which Maxwell made his first attempt to express Faraday's lines of force in rigorous mathematical form. By 1864 Maxwell had refined his model into his monumental field theory, which demonstrated that light was simply a manifestation of the electromagnetic field, something that Faraday had long suspected (he wrote repeatedly of “ray-vibrations”) but had been unable to prove.

The publication of Maxwell's theory marked a great inflection point between the old physics of Faraday and the new, emerging, highly mathematical style of Maxwell and his successors. While discovering the mechanism through experiment was everything to Faraday, correctly describing the behaviour and correctly predicting the outcome of experiments with a set of equations was all that mattered in the new style, which made no effort to explain why the equations worked. As Heinrich Hertz said, “Maxwell's theory is Maxwell's equations” (p. 190). Michael Faraday lived in an era in which a humble-born person with no formal education or knowledge of advanced mathematics could, purely through intelligence, assiduous self-study, clever and tireless experimentation with simple apparatus he made with his own hands, make fundamental discoveries about the universe and rise to the top rank of scientists. Those days are now forever gone, and while we now know vastly more than those of Faraday's time, one also feels we've lost something. Aldous Huxley once remarked, “Even if I could be Shakespeare, I think I should still choose to be Faraday.” This book is an excellent way to appreciate how science felt when it was all new and mysterious, acquaint yourself with one of the most admirable characters in its history, and understand why Huxley felt as he did.

July 2008 

Hoagland, Richard C. and Mike Bara. Dark Mission. Los Angeles: Feral House, 2007. ISBN 1-932595-26-0.

Author Richard C. Hoagland first came to prominence as an “independent researcher” and advocate that “the face on Mars” was an artificially-constructed monument built by an ancient extraterrestrial civilisation. Hoagland has established himself as one of the most indefatigable and imaginative pseudoscientific crackpots on the contemporary scene, and this œuvre pulls it all together into a side-splittingly zany compendium of conspiracy theories, wacky physics, imaginative image interpretation, and feuds within the “anomalist” community—a tempest in a crackpot, if you like.

Hoagland seems to possess a visual system which endows him with a preternatural ability, undoubtedly valuable for an anomalist, of seeing things that aren't there. Now you may look at a print of a picture taken on the lunar surface by an astronaut with a Hasselblad camera and see, in the black lunar sky, negative scratches, film smudges, lens flare, and, in contrast-stretched and otherwise manipulated digitally scanned images, artefacts of the image processing filters applied, but Hoagland immediately perceives “multiple layers of breathtaking ‘structural construction’ embedded in the NASA frame; multiple surviving ‘cell-like rooms,’ three-dimensional ‘cross-bracing,’ angled ‘stringers,’ etc… all following logical structural patterns for a massive work of shattered, but once coherent, glass-like mega-engineering” (p. 153, emphasis in the original). You can see these wonders for yourself on Hoagland's site, The Enterprise Mission. From other Apollo images Hoagland has come to believe that much of the near side of the Moon is covered by the ruins of glass and titanium domes, some which still reach kilometres into the lunar sky and towered over some of the Apollo landing sites.

Now, you might ask, why did the Apollo astronauts not remark upon these prodigies, either while presumably dodging them when landing and flying back to orbit, nor on the surface, nor afterward. Well, you see, they must have been sworn to secrecy at the time and later (p. 176) hypnotised to cause them to forget the obvious evidence of a super-civilisation they were tripping over on the lunar surface. Yeah, that'll work.

Now, Occam's razor advises us not to unnecessarily multiply assumptions when formulating our hypotheses. On the one hand, we have the mainstream view that NASA missions have honestly reported the data they obtained to the public, and that these data, to date, include no evidence (apart from the ambiguous Viking biology tests on Mars) for extraterrestrial life nor artefacts of another civilisation. On the other, Hoagland argues:

• NASA has been, from inception, ruled by three contending secret societies, all of which trace their roots to the gods of ancient Egypt: the Freemasons, unrepentant Nazi SS, and occult disciples of Aleister Crowley.
• These cults have arranged key NASA mission events to occur at “ritual” times, locations, and celestial alignments. The Apollo 16 lunar landing was delayed due to a faked problem with the SPS engine so as to occur on Hitler's birthday.
• John F. Kennedy was assassinated by a conspiracy including Lyndon Johnson and Congressman Albert Thomas of Texas because Kennedy was about to endorse a joint Moon mission with the Soviets, revealing to them the occult reasons behind the Apollo project.
• There are two factions within NASA: the “owls”, who want to hide the evidence from the public, and the “roosters”, who are trying to get it out by covert data releases and cleverly coded clues.

  But wait, there's more!

• The energy of the Sun comes, at least in part, from a “hyperdimensional plane” which couples to rotating objects through gravitational torsion (you knew that was going to come in sooner or later!) This energy expresses itself through a tetrahedral geometry, and explains, among other mysteries, the Great Red Spot of Jupiter, the Great Dark Spot of Neptune, Olympus Mons on Mars, Mauna Kea in Hawaii, and the precession of isolated pulsars.
• The secrets of this hyperdimensional physics, glimpsed by James Clerk Maxwell in his quaternion (check off another crackpot checklist item) formulation of classical electrodynamics, were found by Hoagland to be encoded in the geometry of the “monuments” of Cydonia on Mars.
• Mars was once the moon of a “Planet V”, which exploded (p. 362).

  And that's not all!

• NASA's Mars rover Opportunity imaged a fossil in a Martian rock and then promptly ground it to dust.
• The terrain surrounding the rover Spirit is littered with artificial objects.
• Mars Pathfinder imaged a Sphinx on Mars.

  And if that weren't enough!

• Apollo 17 astronauts photographed the head of an anthropomorphic robot resembling C-3PO lying in Shorty Crater on the Moon (p. 487).

It's like Velikovsky meets The Illuminatus! Trilogy, with some of the darker themes of “Millennium” thrown in for good measure.

Now, I'm sure, as always happens when I post a review like this, the usual suspects are going to write to demand whatever possessed me to read something like this and/or berate me for giving publicity to such hyperdimensional hogwash. Lighten up! I read for enjoyment, and to anybody with a grounding in the Actual Universe™, this stuff is absolutely hilarious: there's a chortle every few pages and a hearty guffaw or two in each chapter. The authors actually write quite well: this is not your usual semi-literate crank-case sludge, although like many on the far fringes of rationality they seem to be unduly challenged by the humble apostrophe. Hoagland is inordinately fond of the word “infamous”, but this becomes rather charming after the first hundred or so, kind of like the verbal tics of your crazy uncle, who Hoagland rather resembles. It's particularly amusing to read the accounts of Hoagland's assorted fallings out and feuds with other “anomalists”; when Tom Van Flandern concludes you're a kook, then you know you're out there, and I don't mean hanging with the truth.

December 2007 

Hossenfelder, Sabine. Lost in Math. New York: Basic Books, 2019. ISBN 978-0-465-09425-7.

Many of the fundamental theories of physics: general relativity, quantum mechanics, and thermodynamics, for example, exhibit great mathematical beauty and elegance once you've mastered the notation in which they are expressed. Some physicists believe that a correct theory must be elegant and beautiful. But what if they're wrong? Many sciences, such as biology and geology, are complicated and messy, with few general principles that don't have exceptions, and in which explanation must take into account a long history of events which might have happened differently. The author, a theoretical physicist, cautions that as her field becomes disconnected from experiment and exploring notions such as string theory and multiple universes, it may be overlooking a reality which, messy though it may be, is the one we actually inhabit and, as scientists, try to understand.

May 2020 

Hoyle, Fred, Geoffrey Burbridge, and Jayant V. Narlikar. A Different Approach to Cosmology. Cambridge: Cambridge University Press, 2000. ISBN 0-521-66223-0.

March 2001 

Kaiser, David. How the Hippies Saved Physics. New York: W. W. Norton, 2011. ISBN 978-0-393-07636-3.

From its origin in the early years of the twentieth century until the outbreak of World War II, quantum theory inspired deeply philosophical reflection as to its meaning and implications for concepts rarely pondered before in physics, such as the meaning of “measurement”, the rôle of the “observer”, the existence of an objective reality apart from the result of a measurement, and whether the randomness of quantum measurements was fundamental or due to our lack of knowledge of an underlying stratum of reality. Quantum theory seemed to imply that the universe could not be neatly reduced to isolated particles which interacted only locally, but admitted “entanglement” among separated particles which seemed to verge upon mystic conceptions of “all is one”. These weighty issues occupied the correspondence and conference debates of the pioneers of quantum theory including Planck, Heisenberg, Einstein, Bohr, Schrödinger, Pauli, Dirac, Born, and others.

And then the war came, and then the war came to an end, and with it ended the inquiry into the philosophical foundations of quantum theory. During the conflict, physicists on all sides were central to war efforts including nuclear weapons, guided missiles, radar, and operations research, and after the war they were perceived by governments as a strategic resource—subsidised in their education and research and provided with lavish facilities in return for having them on tap when their intellectual capacities were needed. In this environment, the education and culture of physics underwent a fundamental change. Suddenly the field was much larger than before, filled with those interested more in their own careers than probing the bottom of deep questions, and oriented toward, in Richard Feynman's words, “getting the answer out”. Instead of debating what their equations said about the nature of reality, the motto of the age became “shut up and calculate”, and physicists who didn't found their career prospects severely constrained.

Such was the situation from the end of World War II through the 1960s, when the defence (and later space program) funding gravy train came to an end due to crowding out of R&D budgets by the Vietnam War and the growing financial crisis due to debasement of the dollar. Suddenly, an entire cohort of Ph.D. physicists who, a few years before could expect to choose among a variety of tenure-track positions in academia or posts in government or industry research laboratories, found themselves superbly qualified to do work which nobody seemed willing to pay them to do. Well, whatever you say about physicists, they're nothing if they aren't creative, so a small group of out of the box thinkers in the San Francisco Bay area self-organised into the Fundamental Fysiks Group and began to re-open the deep puzzles in quantum mechanics which had laid fallow since the 1930s. This group, founded by Elizabeth Rauscher and George Weissmann, whose members came to include Henry Stapp, Philippe Eberhard, Nick Herbert, Jack Sarfatti, Saul-Paul Sirag, Fred Alan Wolf, John Clauser, and Fritjof Capra, came to focus on Bell's theorem and its implications for quantum entanglement, what Einstein called “spooky action at a distance”, and the potential for instantaneous communications not limited by the speed of light.

The author argues that the group's work, communicated through samizdat circulation of manuscripts, the occasional publication in mainstream journals, and contact with established researchers open to considering foundational questions, provided the impetus for today's vibrant theoretical and experimental investigation of quantum information theory, computing, and encryption. There is no doubt whatsoever from the trail of citations that Nick Herbert's attempts to create a faster-than-light signalling device led directly to the quantum no-cloning theorem.

Not only did the group reestablish the prewar style of doing physics, more philosophical than computational, they also rediscovered the way science had been funded from the Medicis until the advent of Big Science. While some group members held conventional posts, others were supported by wealthy patrons interested in their work purely from its intellectual value. We encounter a variety of characters who probably couldn't have existed in any decade other than the 1970s including Werner Erhard, Michael Murphy, Ira Einhorn, and Uri Geller.

The group's activities ranged far beyond the classrooms and laboratories into which postwar physics had been confined, to the thermal baths at Esalen and outreach to the public through books which became worldwide bestsellers and remain in print to this day. Their curiosity also wandered well beyond the conventional bounds of physics, encompassing ESP (and speculating as to how quantum processes might explain it). This caused many mainstream physicists to keep members at arm's length, even as their insights on quantum processes were infiltrating the journals.

Many of us who lived through (I prefer the term “endured”) the 1970s remember them as a dull brown interlude of broken dreams, ugly cars, funny money, and malaise. But, among a small community of thinkers orphaned from the career treadmill of mainstream physics, it was a renaissance of investigation of the most profound questions in physics, and the spark which lit today's research into quantum information processing.

The Kindle edition has the table of contents, and notes properly linked, but the index is just a useless list of terms. An interview of the author, Jack Sarfatti, and Fred Alan Wolf by George Knapp on “Coast to Coast AM” is available.

November 2011 

Kaku, Michio. Hyperspace. New York: Anchor Books, 1994. ISBN 0-385-47705-8.

November 2001 

Kane, Gordon. Supersymmetry. New York: Perseus Publishing, 2000. ISBN 0-7382-0203-7.

April 2001 

Keating, Brian. Losing the Nobel Prize. New York: W. W. Norton, 2018. ISBN 978-1-324-00091-4.

Ever since the time of Galileo, the history of astronomy has been punctuated by a series of “great debates”—disputes between competing theories of the organisation of the universe which observation and experiment using available technology are not yet able to resolve one way or another. In Galileo's time, the great debate was between the Ptolemaic model, which placed the Earth at the centre of the solar system (and universe) and the competing Copernican model which had the planets all revolving around the Sun. Both models worked about as well in predicting astronomical phenomena such as eclipses and the motion of planets, and no observation made so far had been able to distinguish them.

Then, in 1610, Galileo turned his primitive telescope to the sky and observed the bright planets Venus and Jupiter. He found Venus to exhibit phases, just like the Moon, which changed over time. This would not happen in the Ptolemaic system, but is precisely what would be expected in the Copernican model—where Venus circled the Sun in an orbit inside that of Earth. Turning to Jupiter, he found it to be surrounded by four bright satellites (now called the Galilean moons) which orbited the giant planet. This further falsified Ptolemy's model, in which the Earth was the sole source of attraction around which all celestial bodies revolved. Since anybody could build their own telescope and confirm these observations, this effectively resolved the first great debate in favour of the Copernican heliocentric model, although some hold-outs in positions of authority resisted its dethroning of the Earth as the centre of the universe.

This dethroning came to be called the “Copernican principle”, that Earth occupies no special place in the universe: it is one of a number of planets orbiting an ordinary star in a universe filled with a multitude of other stars. Indeed, when Galileo observed the star cluster we call the Pleiades, he saw myriad stars too dim to be visible to the unaided eye. Further, the bright stars were surrounded by a diffuse bluish glow. Applying the Copernican principle again, he argued that the glow was due to innumerably more stars too remote and dim for his telescope to resolve, and then generalised that the glow of the Milky Way was also composed of uncountably many stars. Not only had the Earth been demoted from the centre of the solar system, so had the Sun been dethroned to being just one of a host of stars possibly stretching to infinity.

But Galileo's inference from observing the Pleiades was wrong. The glow that surrounds the bright stars is due to interstellar dust and gas which reflect light from the stars toward Earth. No matter how large or powerful the telescope you point toward such a reflection nebula, all you'll ever see is a smooth glow. Driven by the desire to confirm his Copernican convictions, Galileo had been fooled by dust. He would not be the last.

William Herschel was an eminent musician and composer, but his passion was astronomy. He pioneered the large reflecting telescope, building more than sixty telescopes. In 1789, funded by a grant from King George III, Herschel completed a reflector with a mirror 1.26 metres in diameter, which remained the largest aperture telescope in existence for the next fifty years. In Herschel's day, the great debate was about the Sun's position among the surrounding stars. At the time, there was no way to determine the distance or absolute brightness of stars, but Herschel decided that he could compile a map of the galaxy (then considered to be the entire universe) by surveying the number of stars in different directions. Only if the Sun was at the centre of the galaxy would the counts be equal in all directions.

Aided by his sister Caroline, a talented astronomer herself, he eventually compiled a map which indicated the galaxy was in the shape of a disc, with the Sun at the centre. This seemed to refute the Copernican view that there was nothing special about the Sun's position. Such was Herschel's reputation that this finding, however puzzling, remained unchallenged until 1847 when Wilhelm Struve discovered that Herschel's results had been rendered invalid by his failing to take into account the absorption and scattering of starlight by interstellar dust. Just as you can only see the same distance in all directions while within a patch of fog, regardless of the shape of the patch, Herschel's survey could only see so far before extinction of light by dust cut off his view of stars. Later it was discovered that the Sun is far from the centre of the galaxy. Herschel had been fooled by dust.

In the 1920s, another great debate consumed astronomy. Was the Milky Way the entire universe, or were the “spiral nebulæ” other “island universes”, galaxies in their own right, peers of the Milky Way? With no way to measure distance or telescopes able to resolve them into stars, many astronomers believed spiral neublæ were nearby objects, perhaps other solar systems in the process of formation. The discovery of a Cepheid variable star in the nearby Andromeda “nebula” by Edwin Hubble in 1923 allowed settling this debate. Andromeda was much farther away than the most distant stars found in the Milky Way. It must, then be a separate galaxy. Once again, demotion: the Milky Way was not the entire universe, but just one galaxy among a multitude.

But how far away were the galaxies? Hubble continued his search and measurements and found that the more distant the galaxy, the more rapidly it was receding from us. This meant the universe was expanding. Hubble was then able to calculate the age of the universe—the time when all of the galaxies must have been squeezed together into a single point. From his observations, he computed this age at two billion years. This was a major embarrassment: astrophysicists and geologists were confident in dating the Sun and Earth at around five billion years. It didn't make any sense for them to be more than twice as old as the universe of which they were a part. Some years later, it was discovered that Hubble's distance estimates were far understated because he failed to account for extinction of light from the stars he measured due to dust. The universe is now known to be seven times the age Hubble estimated. Hubble had been fooled by dust.

By the 1950s, the expanding universe was generally accepted and the great debate was whether it had come into being in some cataclysmic event in the past (the “Big Bang”) or was eternal, with new matter spontaneously appearing to form new galaxies and stars as the existing ones receded from one another (the “Steady State” theory). Once again, there were no observational data to falsify either theory. The Steady State theory was attractive to many astronomers because it was the more “Copernican”—the universe would appear overall the same at any time in an infinite past and future, so our position in time is not privileged in any way, while in the Big Bang the distant past and future are very different than the conditions we observe today. (The rate of matter creation required by the Steady State theory was so low that no plausible laboratory experiment could detect it.)

The discovery of the cosmic background radiation in 1965 definitively settled the debate in favour of the Big Bang. It was precisely what was expected if the early universe were much denser and hotter than conditions today, as predicted by the Big Bang. The Steady State theory made no such prediction and was, despite rear-guard actions by some of its defenders (invoking dust to explain the detected radiation!), was considered falsified by most researchers.

But the Big Bang was not without its own problems. In particular, in order to end up with anything like the universe we observe today, the initial conditions at the time of the Big Bang seemed to have been fantastically fine-tuned (for example, an infinitesimal change in the balance between the density and rate of expansion in the early universe would have caused the universe to quickly collapse into a black hole or disperse into the void without forming stars and galaxies). There was no physical reason to explain these fine-tuned values; you had to assume that's just the way things happened to be, or that a Creator had set the dial with a precision of dozens of decimal places.

In 1979, the theory of inflation was proposed. Inflation held that in an instant after the Big Bang the size of the universe blew up exponentially so that all the observable universe today was, before inflation, the size of an elementary particle today. Thus, it's no surprise that the universe we now observe appears so uniform. Inflation so neatly resolved the tensions between the Big Bang theory and observation that it (and refinements over the years) became widely accepted. But could inflation be observed? That is the ultimate test of a scientific theory.

There have been numerous cases in science where many years elapsed between a theory being proposed and definitive experimental evidence for it being found. After Galileo's observations, the Copernican theory that the Earth orbits the Sun became widely accepted, but there was no direct evidence for the Earth's motion with respect to the distant stars until the discovery of the aberration of light in 1727. Einstein's theory of general relativity predicted gravitational radiation in 1915, but the phenomenon was not directly detected by experiment until a century later. Would inflation have to wait as long or longer?

Things didn't look promising. Almost everything we know about the universe comes from observations of electromagnetic radiation: light, radio waves, X-rays, etc., with a little bit more from particles (cosmic rays and neutrinos). But the cosmic background radiation forms an impenetrable curtain behind which we cannot observe anything via the electromagnetic spectrum, and it dates from around 380,000 years after the Big Bang. The era of inflation was believed to have ended 10⁻³² seconds after the Bang; considerably earlier. The only “messenger” which could possibly have reached us from that era is gravitational radiation. We've just recently become able to detect gravitational radiation from the most violent events in the universe, but no conceivable experiment would be able to detect this signal from the baby universe.

So is it hopeless? Well, not necessarily…. The cosmic background radiation is a snapshot of the universe as it existed 380,000 years after the Big Bang, and only a few years after it was first detected, it was realised that gravitational waves from the very early universe might have left subtle imprints upon the radiation we observe today. In particular, gravitational radiation creates a form of polarisation called B-modes which most other sources cannot create.

If it were possible to detect B-mode polarisation in the cosmic background radiation, it would be a direct detection of inflation. While the experiment would be demanding and eventually result in literally going to the end of the Earth, it would be strong evidence for the process which shaped the universe we inhabit and, in all likelihood, a ticket to Stockholm for those who made the discovery.

This was the quest on which the author embarked in the year 2000, resulting in the deployment of an instrument called BICEP1 (Background Imaging of Cosmic Extragalactic Polarization) in the Dark Sector Laboratory at the South Pole. Here is my picture of that laboratory in January 2013. The BICEP telescope is located in the foreground inside a conical shield which protects it against thermal radiation from the surrounding ice. In the background is the South Pole Telescope, a millimetre wave antenna which was not involved in this research.

BICEP1 was a prototype, intended to test the technologies to be used in the experiment. These included cooling the entire telescope (which was a modest aperture [26 cm] refractor, not unlike Galileo's, but operating at millimetre wavelengths instead of visible light) to the temperature of interstellar space, with its detector cooled to just ¼ degree above absolute zero. In 2010 its successor, BICEP2, began observation at the South Pole, and continued its run into 2012. When I took the photo above, BICEP2 had recently concluded its observations.

On March 17th, 2014, the BICEP2 collaboration announced, at a press conference, the detection of B-mode polarisation in the region of the southern sky they had monitored. Note the swirling pattern of polarisation which is the signature of B-modes, as opposed to the starburst pattern of other kinds of polarisation.

But, not so fast, other researchers cautioned. The risk in doing “science by press release” is that the research is not subjected to peer review—criticism by other researchers in the field—before publication and further criticism in subsequent publications. The BICEP2 results went immediately to the front pages of major newspapers. Here was direct evidence of the birth cry of the universe and confirmation of a theory which some argued implied the existence of a multiverse—the latest Copernican demotion—the idea that our universe was just one of an ensemble, possibly infinite, of parallel universes in which every possibility was instantiated somewhere. Amid the frenzy, a few specialists in the field, including researchers on competing projects, raised the question, “What about the dust?” Dust again! As it happens, while gravitational radiation can induce B-mode polarisation, it isn't the only thing which can do so. Our galaxy is filled with dust and magnetic fields which can cause those dust particles to align with them. Aligned dust particles cause polarised reflections which can mimic the B-mode signature of the gravitational radiation sought by BICEP2.

The BICEP2 team was well aware of this potential contamination problem. Unfortunately, their telescope was sensitive only to one wavelength, chosen to be the most sensitive to B-modes due to primordial gravitational radiation. It could not, however, distinguish a signal from that cause from one due to foreground dust. At the same time, however, the European Space Agency Planck spacecraft was collecting precision data on the cosmic background radiation in a variety of wavelengths, including one sensitive primarily to dust. Those data would have allowed the BICEP2 investigators to quantify the degree their signal was due to dust. But there was a problem: BICEP2 and Planck were direct competitors.

Planck had the data, but had not released them to other researchers. However, the BICEP2 team discovered that a member of the Planck collaboration had shown a slide at a conference of unpublished Planck observations of dust. A member of the BICEP2 team digitised an image of the slide, created a model from it, and concluded that dust contamination of the BICEP2 data would not be significant. This was a highly dubious, if not explicitly unethical move. It confirmed measurements from earlier experiments and provided confidence in the results.

In September 2014, a preprint from the Planck collaboration (eventually published in 2016) showed that B-modes from foreground dust could account for all of the signal detected by BICEP2. In January 2015, the European Space Agency published an analysis of the Planck and BICEP2 observations which showed the entire BICEP2 detection was consistent with dust in the Milky Way. The epochal detection of inflation had been deflated. The BICEP2 researchers had been deceived by dust.

The author, a founder of the original BICEP project, was so close to a Nobel prize he was already trying to read the minds of the Nobel committee to divine who among the many members of the collaboration they would reward with the gold medal. Then it all went away, seemingly overnight, turned to dust. Some said that the entire episode had injured the public's perception of science, but to me it seems an excellent example of science working precisely as intended. A result is placed before the public; others, with access to the same raw data are given an opportunity to critique them, setting forth their own raw data; and eventually researchers in the field decide whether the original results are correct. Yes, it would probably be better if all of this happened in musty library stacks of journals almost nobody reads before bursting out of the chest of mass media, but in an age where scientific research is funded by agencies spending money taken from hairdressers and cab drivers by coercive governments under implicit threat of violence, it is inevitable they will force researchers into the public arena to trumpet their “achievements”.

In parallel with the saga of BICEP2, the author discusses the Nobel Prizes and what he considers to be their dysfunction in today's scientific research environment. I was surprised to learn that many of the curious restrictions on awards of the Nobel Prize were not, as I had heard and many believe, conditions of Alfred Nobel's will. In fact, the conditions that the prize be shared no more than three ways, not be awarded posthumously, and not awarded to a group (with the exception of the Peace prize) appear nowhere in Nobel's will, but were imposed later by the Nobel Foundation. Further, Nobel's will explicitly states that the prizes shall be awarded to “those who, during the preceding year, shall have conferred the greatest benefit to mankind”. This constraint (emphasis mine) has been ignored since the inception of the prizes.

He decries the lack of “diversity” in Nobel laureates (by which he means, almost entirely, how few women have won prizes). While there have certainly been women who deserved prizes and didn't win (Lise Meitner, Jocelyn Bell Burnell, and Vera Rubin are prime examples), there are many more men who didn't make the three laureates cut-off (Freeman Dyson an obvious example for the 1965 Physics Nobel for quantum electrodynamics). The whole Nobel prize concept is capricious, and rewards only those who happen to be in the right place at the right time in the right field that the committee has decided deserves an award this year and are lucky enough not to die before the prize is awarded. To imagine it to be “fair” or representative of scientific merit is, in the estimation of this scribbler, in flying unicorn territory.

In all, this is a candid view of how science is done at the top of the field today, with all of the budget squabbles, maneuvering for recognition, rivalry among competing groups of researchers, balancing the desire to get things right with the compulsion to get there first, and the eye on that prize, given only to a few in a generation, which can change one's life forever.

Personally, I can't imagine being so fixated on winning a prize one has so little chance of gaining. It's like being obsessed with winning the lottery—and about as likely.

In parallel with all of this is an autobiographical account of the career of a scientist with its ups and downs, which is both a cautionary tale and an inspiration to those who choose to pursue that difficult and intensely meritocratic career path.

I recommend this book on all three tracks: a story of scientific discovery, mis-interpretation, and self-correction, the dysfunction of the Nobel Prizes and how they might be remedied, and the candid story of a working scientist in today's deeply corrupt coercively-funded research environment.

August 2018 

Krauss, Lawrence. Quintessence: The Mystery of Missing Mass in the Universe. New York: Basic Books, 2000. ISBN 0-465-03740-2.

February 2001 

Krauss, Lawrence. Quantum Man. New York: W. W. Norton, 2011. ISBN 978-0-393-34065-5.

A great deal has been written about the life, career, and antics of Richard Feynman, but until the present book there was not a proper scientific biography of his work in physics and its significance in the field and consequences for subsequent research. Lawrence Krauss has masterfully remedied this lacuna with this work, which provides, at a level comprehensible to the intelligent layman, both a survey of Feynman's work, both successful and not, and also a sense of how Feynman achieved what he did and what ultimately motivated him in his often lonely quest to understand.

One often-neglected contributor to Feynman's success is discussed at length: his extraordinary skill in mathematical computation, intuitive sense of the best way to proceed toward a solution (he would often skip several intermediate steps and only fill them in when preparing work for publication), and tireless perseverance in performing daunting calculations which occupied page after page of forbidding equations. This talent was quickly recognised by those with whom he worked, and as one of the most junior physicists on the project, he was placed in charge of all computation at Los Alamos during the final phases of the Manhattan Project. Eugene Wigner said of Feynman, “He's another Dirac. Only this time human.”

Feynman's intuition and computational prowess was best demonstrated by his work on quantum electrodynamics, for which he shared a Nobel prize in 1965. (Initially Feynman didn't think too much of this work—he considered it mathematical mumbo-jumbo which swept the infinities which had plagued earlier attempts at a relativistic quantum theory of light and matter under the carpet. Only later did it become apparent that Feynman's work had laid the foundation upon which a comprehensive quantum field theory of the strong and electroweak interactions could be built.) His invention of Feynman diagrams defined the language now universally used by particle physicists to describe events in which particles interact.

Feynman was driven to understand things, and to him understanding meant being able to derive a phenomenon from first principles. Often he ignored the work of others and proceeded on his own, reinventing as he went. In numerous cases, he created new techniques and provided alternative ways of looking at a problem which provided a deeper insight into its fundamentals. A monumental illustration of Feynman's ability to do this is The Feynman Lectures on Physics, based on an undergraduate course in physics Feynman taught at Caltech in 1961–1964. Few physicists would have had the audacity to reformulate all of basic physics, from vectors and statics to quantum mechanics from scratch, and probably only Feynman could have pulled it off, which he did magnificently. As undergraduate pedagogy, the course was less than successful, but the transcribed lectures have remained in print ever since, and working physicists (and even humble engineers like me) are astounded at the insights to be had in reading and re-reading Feynman's work.

Even when Feynman failed, he failed gloriously and left behind work that continues to inspire. His unsuccessful attempt to find a quantum theory of gravitation showed that Einstein's geometric theory was completely equivalent to a field theory developed from first principles and knowledge of the properties of gravity. Feynman's foray into computation produced the Feynman Lectures On Computation, one of the first comprehensive expositions of the theory of quantum computation.

A chapter is devoted to the predictions of Feynman's 1959 lecture, “Plenty of Room at the Bottom”, which is rightly viewed as the founding document of molecular nanotechnology, but, as Krauss describes, also contained the seeds of genomic biotechnology, ultra-dense data storage, and quantum material engineering. Work resulting in more than fifteen subsequent Nobel prizes is suggested in this blueprint for research. Although Feynman would go on to win his own Nobel for other work, one gets the sense he couldn't care less that others pursued the lines of investigation he sketched and were rewarded for doing so. Feynman was in the game to understand, and often didn't seem to care whether what he was pursuing was of great importance or mundane, or whether the problem he was working on from his own unique point of departure had already been solved by others long before.

Feynman was such a curious character that his larger than life personality often obscures his greatness as a scientist. This book does an excellent job of restoring that balance and showing how much his work contributed to the edifice of science in the 20th century and beyond.

April 2013 

Levenson, Thomas. The Hunt for Vulcan. New York: Random House, 2015. ISBN 978-0-8129-9898-6.

The history of science has been marked by discoveries in which, by observing where nobody had looked before, with new and more sensitive instruments, or at different aspects of reality, new and often surprising phenomena have been detected. But some of the most profound of our discoveries about the universe we inhabit have come from things we didn't observe, but expected to.

By the nineteenth century, one of the most solid pillars of science was Newton's law of universal gravitation. With a single equation a schoolchild could understand, it explained why objects fall, why the Moon orbits the Earth and the Earth and other planets the Sun, the tides, and the motion of double stars. But still, one wonders: is the law of gravitation exactly as Newton described, and does it work everywhere? For example, Newton's gravity gets weaker as the inverse square of the distance between two objects (for example, if you double the distance, the gravitational force is four times weaker [2² = 4]) but has unlimited range: every object in the universe attracts every other object, however weakly, regardless of distance. But might gravity not, say, weaken faster at great distances? If this were the case, the orbits of the outer planets would differ from the predictions of Newton's theory. Comparing astronomical observations to calculated positions of the planets was a way to discover such phenomena.

In 1781 astronomer William Herschel discovered Uranus, the first planet not known since antiquity. (Uranus is dim but visible to the unaided eye and doubtless had been seen innumerable times, including by astronomers who included it in star catalogues, but Herschel was the first to note its non-stellar appearance through his telescope, originally believing it a comet.) Herschel wasn't looking for a new planet; he was observing stars for another project when he happened upon Uranus. Further observations of the object confirmed that it was moving in a slow, almost circular orbit, around twice the distance of Saturn from the Sun.

Given knowledge of the positions, velocities, and masses of the planets and Newton's law of gravitation, it should be possible to predict the past and future motion of solar system bodies for an arbitrary period of time. Working backward, comparing the predicted influence of bodies on one another with astronomical observations, the masses of the individual planets can be estimated to produce a complete model of the solar system. This great work was undertaken by Pierre-Simon Laplace who published his Mécanique céleste in five volumes between 1799 and 1825. As the middle of the 19th century approached, ongoing precision observations of the planets indicated that all was not proceeding as Laplace had foreseen. Uranus, in particular, continued to diverge from where it was expected to be after taking into account the gravitational influence upon its motion by Saturn and Jupiter. Could Newton have been wrong, and the influence of gravity different over the vast distance of Uranus from the Sun?

In the 1840s two mathematical astronomers, Urbain Le Verrier in France and John Couch Adams in Britain, working independently, investigated the possibility that Newton was right, but that an undiscovered body in the outer solar system was responsible for perturbing the orbit of Uranus. After almost unimaginably tedious calculations (done using tables of logarithms and pencil and paper arithmetic), both Le Verrier and Adams found a solution and predicted where to observe the new planet. Adams failed to persuade astronomers to look for the new world, but Le Verrier prevailed upon an astronomer at the Berlin Observatory to try, and Neptune was duly discovered within one degree (twice the apparent size of the full Moon) of his prediction.

This was Newton triumphant. Not only was the theory vindicated, it had been used, for the first time in history, to predict the existence of a previously unknown planet and tell the astronomers right where to point their telescopes to observe it. The mystery of the outer solar system had been solved. But problems remained much closer to the Sun.

The planet Mercury orbits the Sun every 88 days in an eccentric orbit which never exceeds half the Earth's distance from the Sun. It is a small world, with just 6% of the Earth's mass. As an inner planet, Mercury never appears more than 28° from the Sun, and can best be observed in the morning or evening sky when it is near its maximum elongation from the Sun. (With a telescope, it is possible to observe Mercury in broad daylight.) Flush with his success with Neptune, and rewarded with the post of director of the Paris Observatory, in 1859 Le Verrier turned his attention toward Mercury.

Again, through arduous calculations (by this time Le Verrier had a building full of minions to assist him, but so grueling was the work and so demanding a boss was Le Verrier that during his tenure at the Observatory 17 astronomers and 46 assistants quit) the influence of all of the known planets upon the motion of Mercury was worked out. If Mercury orbited a spherical Sun without other planets tugging on it, the point of its closest approach to the Sun (perihelion) in its eccentric orbit would remain fixed in space. But with the other planets exerting their gravitational influence, Mercury's perihelion should advance around the Sun at a rate of 526.7 arcseconds per century. But astronomers who had been following the orbit of Mercury for decades measured the actual advance of the perihelion as 565 arcseconds per century. This left a discrepancy of 38.3 arcseconds, for which there was no explanation. (The modern value, based upon more precise observations over a longer period of time, for the perihelion precession of Mercury is 43 arcseconds per century.) Although small (recall that there are 1,296,000 arcseconds in a full circle), this anomalous precession was much larger than the margin of error in observations and clearly indicated something was amiss. Could Newton be wrong?

Le Verrier thought not. Just as he had done for the anomalies of the orbit of Uranus, Le Verrier undertook to calculate the properties of an undiscovered object which could perturb the orbit of Mercury and explain the perihelion advance. He found that a planet closer to the Sun (or a belt of asteroids with equivalent mass) would do the trick. Such an object, so close to the Sun, could easily have escaped detection, as it could only be readily observed during a total solar eclipse or when passing in front of the Sun's disc (a transit). Le Verrier alerted astronomers to watch for transits of this intra-Mercurian planet.

On March 26, 1859, Edmond Modeste Lescarbault, a provincial physician in a small town and passionate amateur astronomer turned his (solar-filtered) telescope toward the Sun. He saw a small dark dot crossing the disc of the Sun, taking one hour and seventeen minutes to transit, just as expected by Le Verrier. He communicated his results to the great man, and after a visit and detailed interrogation, the astronomer certified the doctor's observation as genuine and computed the orbit for the new planet. The popular press jumped upon the story. By February 1860, planet Vulcan was all the rage.

Other observations began to arrive, both from credible and unknown observers. Professional astronomers mounted worldwide campaigns to observe the Sun around the period of predicted transits of Vulcan. All of the planned campaigns came up empty. Searches for Vulcan became a major focus of solar eclipse expeditions. Unless the eclipse happened to occur when Vulcan was in conjunction with the Sun, it should be readily observable when the Sun was obscured by the Moon. Eclipse expeditions prepared detailed star charts for the vicinity of the Sun to exclude known stars for the search during the fleeting moments of totality. In 1878, an international party of eclipse chasers including Thomas Edison descended on Rawlins, Wyoming to hunt Vulcan in an eclipse crossing that frontier town. One group spotted Vulcan; others didn't. Controversy and acrimony ensued.

After 1878, most professional astronomers lost interest in Vulcan. The anomalous advance of Mercury's perihelion was mostly set aside as “one of those things we don't understand”, much as astronomers regard dark matter today. In 1915, Einstein published his theory of gravitation: general relativity. It predicted that when objects moved rapidly or gravitational fields were strong, their motion would deviate from the predictions of Newton's theory. Einstein recalled the moment when he performed the calculation of the motion of Mercury in his just-completed theory. It predicted precisely the perihelion advance observed by the astronomers. He said that his heart shuddered in his chest and that he was “beside himself with joy.”

Newton was wrong! For the extreme conditions of Mercury's orbit, so close to the Sun, Einstein's theory of gravitation is required to obtain results which agree with observation. There was no need for planet Vulcan, and now it is mostly forgotten. But the episode is instructive as to how confidence in long-accepted theories and wishful thinking can lead us astray when what might be needed is an overhaul of our most fundamental theories. A century hence, which of our beliefs will be viewed as we regard planet Vulcan today?

January 2016 

Levin, Janna. Black Hole Blues. New York: Alfred A. Knopf, 2016. ISBN 978-0-307-95819-8.

In Albert Einstein's 1915 general theory of relativity, gravitation does not propagate instantaneously as it did in Newton's theory, but at the speed of light. According to relativity, nothing can propagate faster than light. This has a consequence which was not originally appreciated when the theory was published: if you move an object here, its gravitational influence upon an object there cannot arrive any faster than a pulse of light travelling between the two objects. But how is that change in the gravitational field transmitted? For light, it is via the electromagnetic field, which is described by Maxwell's equations and implies the existence of excitations of the field which, according to their wavelength, we call radio, light, and gamma rays. Are there, then, equivalent excitations of the gravitational field (which, according to general relativity, can be thought of as curvature of spacetime), which transmit the changes due to motion of objects to distant objects affected by their gravity and, if so, can we detect them? By analogy to electromagnetism, where we speak of electromagnetic waves or electromagnetic radiation, these would be gravitational waves or gravitational radiation.

Einstein first predicted the existence of gravitational waves in a 1916 paper, but he made a mathematical error in the nature of sources and the magnitude of the effect. This was corrected in a paper he published in 1918 which describes gravitational radiation as we understand it today. According to Einstein's calculations, gravitational waves were real, but interacted so weakly that any practical experiment would never be able to detect them. If gravitation is thought of as the bending of spacetime, the equations tell us that spacetime is extraordinarily stiff: when you encounter an equation with the speed of light, c, raised to the fourth power in the denominator, you know you're in trouble trying to detect the effect.

That's where the matter rested for almost forty years. Some theorists believed that gravitational waves existed but, given the potential sources we knew about (planets orbiting stars, double and multiple star systems), the energy emitted was so small (the Earth orbiting the Sun emits a grand total of 200 watts of energy in gravitational waves, which is absolutely impossible to detect with any plausible apparatus), we would never be able to detect it. Other physicists doubted the effect was real, and that gravitational waves actually carried energy which could, even in principle, produce effects which could be detected. This dispute was settled to the satisfaction of most theorists by the sticky bead argument, proposed in 1957 by Richard Feynman and Hermann Bondi. Although a few dissenters remained, most of the small community interested in general relativity agreed that gravitational waves existed and could carry energy, but continued to believe we'd probably never detect them.

This outlook changed in the 1960s. Radio astronomers, along with optical astronomers, began to discover objects in the sky which seemed to indicate the universe was a much more violent and dynamic place than had been previously imagined. Words like “quasar”, “neutron star”, “pulsar”, and “black hole” entered the vocabulary, and suggested there were objects in the universe where gravity might be so strong and motion so fast that gravitational waves could be produced which might be detected by instruments on Earth.

Joseph Weber, an experimental physicist at the University of Maryland, was the first to attempt to detect gravitational radiation. He used large bars, now called Weber bars, of aluminium, usually cylinders two metres long and one metre in diameter, instrumented with piezoelectric sensors. The bars were, based upon their material and dimensions, resonant at a particular frequency, and could detect a change in length of the cylinder of around 10⁻¹⁶ metres. Weber was a pioneer in reducing noise of his detectors, and operated two detectors at different locations so that signals would only be considered valid if observed nearly simultaneously by both.

What nobody knew was how “noisy” the sky was in gravitational radiation: how many sources there were and how strong they might be. Theorists could offer little guidance: ultimately, you just had to listen. Weber listened, and reported signals he believed consistent with gravitational waves. But others who built comparable apparatus found nothing but noise and theorists objected that if objects in the universe emitted as much gravitational radiation as Weber's detections implied, it would convert all of its mass into gravitational radiation in just fifty million years. Weber's claims of having detected gravitational radiation are now considered to have been discredited, but there are those who dispute this assessment. Still, he was the first to try, and made breakthroughs which informed subsequent work.

Might there be a better way, which could detect even smaller signals than Weber's bars, and over a wider frequency range? (Since the frequency range of potential sources was unknown, casting the net as widely as possible made more potential candidate sources accessible to the experiment.) Independently, groups at MIT, the University of Glasgow in Scotland, and the Max Planck Institute in Germany began to investigate interferometers as a means of detecting gravitational waves. An interferometer had already played a part in confirming Einstein's special theory of relativity: could it also provide evidence for an elusive prediction of the general theory?

An interferometer is essentially an absurdly precise ruler where the markings on the scale are waves of light. You send beams of light down two paths, and adjust them so that the light waves cancel (interfere) when they're combined after bouncing back from mirrors at the end of the two paths. If there's any change in the lengths of the two paths, the light won't interfere precisely, and its intensity will increase depending upon the difference. But when a gravitational wave passes, that's precisely what happens! Lengths in one direction will be squeezed while those orthogonal (at a right angle) will be stretched. In principle, an interferometer can be an exquisitely sensitive detector of gravitational waves. The gap between principle and practice required decades of diligent toil and hundreds of millions of dollars to bridge.

From the beginning, it was clear it would not be easy. The field of general relativity (gravitation) had been called “a theorist's dream, an experimenter's nightmare”, and almost everybody working in the area were theorists: all they needed were blackboards, paper, pencils, and lots of erasers. This was “little science”. As the pioneers began to explore interferometric gravitational wave detectors, it became clear what was needed was “big science”: on the order of large particle accelerators or space missions, with budgets, schedules, staffing, and management comparable to such projects. This was a culture shock to the general relativity community as violent as the astrophysical sources they sought to detect. Between 1971 and 1989, theorists and experimentalists explored detector technologies and built prototypes to demonstrate feasibility. In 1989, a proposal was submitted to the National Science Foundation to build two interferometers, widely separated geographically, with an initial implementation to prove the concept and a subsequent upgrade intended to permit detection of gravitational radiation from anticipated sources. After political battles, in 1995 construction of LIGO, the Laser Interferometer Gravitational-Wave Observatory, began at the two sites located in Livingston, Louisiana and Hanford, Washington, and in 2001, commissioning of the initial detectors was begun; this would take four years. Between 2005 and 2007 science runs were made with the initial detectors; much was learned about sources of noise and the behaviour of the instrument, but no gravitational waves were detected.

Starting in 2007, based upon what had been learned so far, construction of the advanced interferometer began. This took three years. Between 2010 and 2012, the advanced components were installed, and another three years were spent commissioning them: discovering their quirks, fixing problems, and increasing sensitivity. Finally, in 2015, observations with the advanced detectors began. The sensitivity which had been achieved was astonishing: the interferometers could detect a change in the length of their four kilometre arms which was one ten-thousandth the diameter of a proton (the nucleus of a hydrogen atom). In order to accomplish this, they had to overcome noise which ranged from distant earthquakes, traffic on nearby highways, tides raised in the Earth by the Sun and Moon, and a multitude of other sources, via a tower of technology which made the machine, so simple in concept, forbiddingly complex.

September 14, 2015, 09:51 UTC: Chirp!

A hundred years after the theory that predicted it, 44 years after physicists imagined such an instrument, 26 years after it was formally proposed, 20 years after it was initially funded, a gravitational wave had been detected, and it was right out of the textbook: the merger of two black holes with masses around 29 and 36 times that of the Sun, at a distance of 1.3 billion light years. A total of three solar masses were converted into gravitational radiation: at the moment of the merger, the gravitational radiation emitted was 50 times greater than the light from all of the stars in the universe combined. Despite the stupendous energy released by the source, when it arrived at Earth it could only have been detected by the advanced interferometer which had just been put into service: it would have been missed by the initial instrument and was orders of magnitude below the noise floor of Weber's bar detectors.

For only the third time since proto-humans turned their eyes to the sky a new channel of information about the universe we inhabit was opened. Most of what we know comes from electromagnetic radiation: light, radio, microwaves, gamma rays, etc. In the 20th century, a second channel opened: particles. Cosmic rays and neutrinos allow exploring energetic processes we cannot observe in any other way. In a real sense, neutrinos let us look inside the Sun and into the heart of supernovæ and see what's happening there. And just last year the third channel opened: gravitational radiation. The universe is almost entirely transparent to gravitational waves: that's why they're so difficult to detect. But that means they allow us to explore the universe at its most violent: collisions and mergers of neutron stars and black holes—objects where gravity dominates the forces of the placid universe we observe through telescopes. What will we see? What will we learn? Who knows? If experience is any guide, we'll see things we never imagined and learn things even the theorists didn't anticipate. The game is afoot! It will be a fine adventure.

Black Hole Blues is the story of gravitational wave detection, largely focusing upon LIGO and told through the eyes of Rainer Weiss and Kip Thorne, two of the principals in its conception and development. It is an account of the transition of a field of research from a theorist's toy to Big Science, and the cultural, management, and political problems that involves. There are few examples in experimental science where so long an interval has elapsed, and so much funding expended, between the start of a project and its detecting the phenomenon it was built to observe. The road was bumpy, and that is documented here.

I found the author's tone off-putting. She, a theoretical cosmologist at Barnard College, dismisses scientists with achievements which dwarf her own and ideas which differ from hers in the way one expects from Social Justice Warriors in the squishier disciplines at the Seven Sisters: “the notorious Edward Teller”, “Although Kip [Thorne] outgrew the tedious moralizing, the sexism, and the religiosity of his Mormon roots”, (about Joseph Weber) “an insane, doomed, impossible bar detector designed by the old mad guy, crude laboratory-scale slabs of metal that inspired and encouraged his anguished claims of discovery”, “[Stephen] Hawking made his oddest wager about killer aliens or robots or something, which will not likely ever be resolved, so that might turn out to be his best bet yet”, (about Richard Garwin) “He played a role in halting the Star Wars insanity as well as potentially disastrous industrial escalations, like the plans for supersonic airplanes…”, and “[John Archibald] Wheeler also was not entirely against the House Un-American Activities Committee. He was not entirely against the anticommunist fervor that purged academics from their ivory-tower ranks for crimes of silence, either.” … “I remember seeing him at the notorious Princeton lunches, where visitors are expected to present their research to the table. Wheeler was royalty, in his eighties by then, straining to hear with the help of an ear trumpet. (Did I imagine the ear trumpet?)”. There are also a number of factual errors (for example, a breach in the LIGO beam tube sucking out all of the air from its enclosure and suffocating anybody inside), which a moment's calculation would have shown was absurd.

The book was clearly written with the intention of being published before the first detection of a gravitational wave by LIGO. The entire story of the detection, its validation, and public announcement is jammed into a seven page epilogue tacked onto the end. This epochal discovery deserves being treated at much greater length.

May 2016 

Lindley, David. Degrees Kelvin. Washington: Joseph Henry Press, 2004. ISBN 0-309-09618-9.

When 17 year old William Thomson arrived at Cambridge University to study mathematics, Britain had become a backwater of research in science and mathematics—despite the technologically-driven industrial revolution being in full force, little had been done to build upon the towering legacy of Newton, and cutting edge work had shifted to the Continent, principally France and Germany. Before beginning his studies at Cambridge, Thomson had already published three research papers in the Cambridge Mathematical Journal, one of which introduced Fourier's mathematical theory of heat to English speaking readers, defending it against criticism from those opposed to the highly analytical French style of science which Thomson found congenial to his way of thinking.

Thus began a career which, by the end of the 19th century, made Thomson widely regarded as the preeminent scientist in the world: a genuine scientific celebrity. Over his long career Thomson fused the mathematical rigour of the Continental style of research with the empirical British attitude and made fundamental progress in the kinetic theory of heat, translated Michael Faraday's intuitive view of electricity and magnetism into a mathematical framework which set the stage for Maxwell's formal unification of the two in electromagnetic field theory, and calculated the age of the Earth based upon heat flow from the interior. The latter calculation, in which he estimated only 20 to 40 million years, proved to be wrong, but was so because he had no way to know about radioactive decay as the source of Earth's internal heat: he was explicit in stating that his result assumed no then-unknown source of heat or, as we'd now say, “no new physics”. Such was his prestige that few biologists and geologists whose own investigations argued for a far more ancient Earth stepped up and said, “Fine—so start looking for the new physics!” With Peter Tait, he wrote the Treatise on Natural Philosophy, the first unified exposition of what we would now call classical physics.

Thomson believed that science had to be founded in observations of phenomena, then systematised into formal mathematics and tested by predictions and experiments. To him, understanding the mechanism, ideally based upon a mechanical model, was the ultimate goal. Although acknowledging that Maxwell's equations correctly predicted electromagnetic phenomena, he considered them incomplete because they didn't explain how or why electricity and magnetism behaved that way. Heaven knows what he would have thought of quantum mechanics (which was elaborated after his death in 1907).

He'd probably have been a big fan of string theory, though. Never afraid to add complexity to his mechanical models, he spent two decades searching for a set of 21 parameters which would describe the mechanical properties of the luminiferous ether—what string “landscape” believers might call the moduli and fluxes of the vacuum, and argued for a “vortex atom” model in which extended vortex loops replaced pointlike billiard ball atoms to explain spectrographic results. These speculations proved, as they say, not even wrong.

Thomson was not an ivory tower theorist. He viewed the occupation of the natural philosopher (he disliked the word “physicist”) as that of a problem solver, with the domain of problems encompassing the practical as well as fundamental theory. He was a central figure in the development of the first transatlantic telegraphic cable and invented the mirror galvanometer which made telegraphy over such long distances possible. He was instrumental in defining the units of electricity we still use today. He invented a mechanical analogue computer for computation of tide tables, and a compass compensated for the magnetic distortion of iron and steel warships which became the standard for the Royal Navy. These inventions made him wealthy, and he indulged his love of the sea by buying a 126 ton schooner and inviting his friends and colleagues on voyages.

In 1892, he was elevated to a peerage by Queen Victoria, made Baron Kelvin of Largs, the first scientist ever so honoured. (Numerous scientists, including Newton and Thomson himself in 1866 had been knighted, but the award of a peerage is an honour of an entirely different order.) When he died in 1907 at age 83, he was buried in Westminster Abbey next to the grave of Isaac Newton. For one who accomplished so much, and was so celebrated in his lifetime, Lord Kelvin is largely forgotten today, remembered mostly for the absolute temperature scale named in his honour and, perhaps, for the Kelvinator company of Detroit, Michigan which used his still-celebrated name to promote their ice-boxes and refrigerators. While Thomson had his hand in much of the creation of the edifice of classical physics in the 19th century, there isn't a single enduring piece of work you can point to which is entirely his. This isn't indicative of any shortcoming on his part, but rather of the maturation of science from rare leaps of insight by isolated geniuses to a collective endeavour by an international community reading each other's papers and building a theory by the collaborative effort of many minds. Science was growing up, and Kelvin's reputation has suffered, perhaps, not due to any shortcomings in his contributions, but because they were so broad, as opposed to being identified with a single discovery which was entirely his own.

This is a delightful biography of a figure whose contributions to our knowledge of the world we live in are little remembered. Lord Kelvin never wavered from his belief that science consisted in collecting the data, developing a model and theory to explain what was observed, and following the implications of that theory to their logical conclusions. In doing so, he was often presciently right and occasionally spectacularly wrong, but he was always true to science as he saw it, which is how most scientists see their profession today.

Amusingly, the chapter titles are:

1. Cambridge
2. Conundrums
3. Cable
4. Controversies
5. Compass
6. Kelvin

September 2007 

Lloyd, Seth. Programming the Universe. New York: Alfred A. Knopf, 2006. ISBN 1-4000-4092-2.

The author has devoted his professional career to exploring the deep connections between information processing and the quantum mechanical foundations of the universe. Although his doctorate is in physics, he is a professor of mechanical engineering at MIT, which I suppose makes him an honest to God quantum mechanic. A pioneer in the field of quantum computation, he suggested the first physically realisable quantum computational device, and is author of the landmark papers which evaluated the computational power of the “ultimate laptop”computer which, if its one kilogram of mass and one litre of volume crunched any faster, would collapse into a black hole; estimated the computational capacity of the entire visible universe; and explored how gravitation and spacetime could be emergent properties of a universal quantum computation.

In this book, he presents these concepts to a popular audience, beginning by explaining the fundamentals of quantum mechanics and the principles of quantum computation, before moving on to the argument that the universe as a whole is a universal quantum computer whose future cannot be predicted by any simulation less complicated than the universe as a whole, nor any faster than the future actually evolves (a concept reminiscent of Stephen Wolfram's argument in A New Kind of Science [August 2002], but phrased in quantum mechanical rather than classical terms). He argues that all of the complexity we observe in the universe is the result of the universe performing a computation whose input is the random fluctuations created by quantum mechanics. But, unlike the proverbial monkeys banging on typewriters, the quantum mechanical primate fingers are, in effect, typing on the keys of a quantum computer which, like the cellular automata of Wolfram's book, has the capacity to generate extremely complex structures from very simple inputs. Why was the universe so simple shortly after the big bang? Because it hadn't had the time to compute very much structure. Why is the universe so complicated today? Because it's had sufficient time to perform 10¹²² logical operations up to the present.

I found this book, on the whole, a disappointment. Having read the technical papers cited above before opening it, I didn't expect to learn any additional details from a popularisation, but I did hope the author would provide a sense for how the field evolved and get a sense of where he saw this research programme going in the future and how it might (or might not) fit with other approaches to the unification of quantum mechanics and gravitation. There are some interesting anecdotes about the discovery of the links between quantum mechanics, thermodynamics, statistical mechanics, and information theory, and the personalities involved in that work, but one leaves the book without any sense for where future research might be going, nor how these theories might be tested by experiment in the near or even distant future. The level of the intended audience is difficult to discern. Unlike some popularisers of science, Lloyd does not shrink from using equations where they clarify physical relationships and even introduces and uses Dirac's “bra-ket” notation (for example, <φ|ψ>), yet almost everywhere he writes a number in scientific notation, he also gives it in the utterly meaningless form of (p. 165) “100 billion billion billion billion billion billion billion billion billion billion” (OK, I've done that myself, on one occasion, but I was having fun at the expense of a competitor). And finally, I find it dismaying that a popular science book by a prominent researcher published by a house as respectable as Knopf at a cover price of USD26 lacks an index—this is a fundamental added value that the reader deserves when parting with this much money (especially for a book of only 220 pages). If you know nothing about these topics, this volume will probably leave you only more confused, and possibly over-optimistic about the state of quantum computation. If you've followed the field reasonably closely, the author's professional publications (most available on-line), which are lucidly written and accessible to the non-specialist, may be more rewarding.

I remain dubious about grandiose claims for quantum computation, and nothing in this book dispelled my scepticism. From Democritus all the way to the present day, every single scientific theory which assumed the existence of a continuum has been proved wrong when experiments looked more closely at what was really going on. Yet quantum mechanics, albeit a statistical theory at the level of measurement, is completely deterministic and linear in the evolution of the wave function, with amplitudes given by continuous complex values which embody, theoretically, an infinite amount of information. Where is all this information stored? The Bekenstein bound gives an upper limit on the amount of information which can be represented in a given volume of spacetime, and that implies that even if the quantum state were stored nonlocally in the entire causally connected universe, the amount of information would be (albeit enormous), still finite. Extreme claims for quantum computation assume you can linearly superpose any number of wave functions and thus encode as much information as you like in a single computation. The entire history of science, and of quantum mechanics itself makes me doubt that this is so—I'll bet that we eventually find some inherent granularity in the precision of the wave function (perhaps round-off errors in the simulation we're living within, but let's not revisit that). This is not to say, nor do I mean to imply, that quantum computation will not work; indeed, it has already been demonstrated in proof of concept laboratory experiments, and it may well hold the potential of extending the growth of computational power after the pure scaling of classical computers runs into physical limits. But just as shrinking semiconductor devices is fundamentally constrained by the size of atoms, quantum computation may be limited by the ultimate precision of the discrete computational substrate of the universe which behaves, on the large scale, like a continuous wave function.

July 2006 

Magueijo, João. Faster Than the Speed of Light. Cambridge, MA: Perseus Books, 2003. ISBN 0-7382-0525-7.

January 2003 

Magueijo, João. A Brilliant Darkness. New York: Basic Books, 2009. ISBN 978-0-465-00903-9.

Ettore Majorana is one of the most enigmatic figures in twentieth century physics. The son of a wealthy Sicilian family and a domineering mother, he was a mathematical prodigy who, while studying for a doctorate in engineering, was recruited to join Enrico Fermi's laboratory: the “Via Panisperna boys”. (Can't read that without seeing “panspermia”? Me neither.) Majorana switched to physics, and received his doctorate at the age of 22.

At Fermi's lab, he almost immediately became known as the person who could quickly solve intractable mathematical problems others struggled with for weeks. He also acquired a reputation for working on whatever interested him, declining to collaborate with others. Further, he would often investigate a topic to his own satisfaction, speak of his conclusions to his colleagues, but never get around to writing a formal article for publication—he seemed almost totally motivated by satisfying his own intellectual curiosity and not at all by receiving credit for his work. This infuriated his fiercely competitive boss Fermi, who saw his institute scooped on multiple occasions by others who independently discovered and published work Majorana had done and left to languish in his desk drawer or discarded as being “too obvious to publish”. Still, Fermi regarded Majorana as one of those wild talents who appear upon rare occasions in the history of science. He said,

There are many categories of scientists, people of second and third rank, who do their best, but do not go very far. There are also people of first class, who make great discoveries, which are of capital importance for the development of science. But then there are the geniuses, like Galileo and Newton. Well, Ettore was one of these.

In 1933, Majorana visited Werner Heisenberg in Leipzig and quickly became a close friend of this physicist who was, in most personal traits, his polar opposite. Afterward, he returned to Rome and flip-flopped from his extroversion in the company of Heisenberg to the life of a recluse, rarely leaving his bedroom in the family mansion for almost four years. Then something happened, and he jumped into the competition for the position of full professor at the University of Naples, bypassing the requirement for an examination due to his “exceptional merit”. He emerged from his reclusion, accepted the position, and launched into his teaching career, albeit giving lectures at a level which his students often found bewildering.

Then, on March 26th, 1938, he boarded a ship in Palermo Sicily bound for Naples and was never seen again. Before his departure he had posted enigmatic letters to his employer and family, sent a telegram, and left a further letter in his hotel room which some interpreted as suicide notes, but which forensic scientists who have read thousands of suicide notes say resemble none they've ever seen (but then, would a note by a Galileo or Newton read like that of the run of the mill suicide?). This event set in motion investigation and speculation which continues to this very day. Majorana was said to have withdrawn a large sum of money from his bank a few days before: is this plausible for one bent on self-annihilation (we'll get back to that infra)? Based on his recent interest in religion and reports of his having approached religious communities to join them, members of his family spent a year following up reports that he'd joined a monastery; despite “sightings”, none of these leads panned out. Years later, multiple credible sources with nothing apparently to gain reported that Majorana had been seen on numerous occasions in Argentina, and, abandoning physics (which he had said “was on the wrong path” before his disappearance), pursued a career as an engineer.

This only scratches the surface of the legends which have grown up around Majorana. His disappearance, occurring after nuclear fission had already been produced in Fermi's laboratory, but none of the “boys” had yet realised what they'd seen, spawns speculation that Majorana, as he often did, figured it out, worked out the implications, spoke of it to someone, and was kidnapped by the Germans (maybe he mentioned it to his friend Heisenberg), the Americans, or the Soviets. There is an Italian comic book in which Majorana is abducted by Americans, spirited off to Los Alamos to work on the Manhattan Project, only to be abducted again (to his great relief) by aliens in a flying saucer. Nobody knows—this is just one of the many mysteries bearing the name Majorana.

Today, Majorana is best known for his work on the neutrino. He responded to Paul Dirac's theory of the neutrino (which he believed unnecessarily complicated and unphysical) with his own, in which, as opposed to there being neutrinos and antineutrinos, the neutrino is its own antiparticle and hence neutrinos of the same flavour can annihilate one another. At the time these theories were proposed the neutrino had not been detected, nor would it be for twenty years. When the existence of the neutrino was confirmed (although few doubted its existence by the time Reines and Cowan detected it in 1956), few believed it would ever be possible to distinguish the Dirac and Majorana theories of the neutrino, because that particle was almost universally believed to be massless. But then the “scientific consensus” isn't always the way to bet.

Starting with solar neutrino experiments in the 1960s, and continuing to the present day, it became clear that neutrinos did have mass, albeit very little compared to the electron. This meant that the distinction between the Dirac and Majorana theories of the neutrino was accessible to experiment, and could, at least in principle, be resolved. “At least in principle”: what a clarion call to the bleeding edge experimentalist! If the neutrino is a Majorana particle, as opposed to a Dirac particle, then neutrinoless double beta decay should occur, and we'll know whether Majorana's model, proposed more than seven decades ago, was correct. I wish there'd been more discussion of the open controversy over experiments which claim a 6σ signal for neutrinoless double beta decay in ⁷⁶Ge, but then one doesn't want to date one's book with matters actively disputed.

To the book: this may be the first exemplar of a new genre I'll dub “gonzo scientific biography”. Like the “new journalism” of the 1960s and '70s, this is as much about the author as the subject; the author figures as a central character in the narrative, whether transcribing his queries in pidgin Italian to the Majorana family:

“Signora wifed a brother of Ettore, Luciano?”
“What age did signora owned at that time”
“But he was olded fifty years!”
“But in end he husbanded you.”

Besides humourously trampling on the language of Dante, the author employs profanity as a superlative as do so many “new journalists”. I find this unseemly in a scientific biography of an ascetic, deeply-conflicted individual who spent most of his short life in a search for the truth and, if he erred, erred always on the side of propriety, self-denial, and commitment to dignity of all people.

Should you read this? Well, if you've come this far, of course you should!   This is an excellent, albeit flawed, biography of a singular, albeit flawed, genius whose intellectual legacy motivates massive experiments conducted deep underground and in the seas today. Suppose a neutrinoless double beta decay experiment should confirm the Majorana theory? Should he receive the Nobel prize for it? On the merits, absolutely: many physics Nobels have been awarded for far less, and let's not talk about the “soft Nobels”. But under the rules a Nobel prize can't be awarded posthumously. Which then compels one to ask, “Is Ettore dead?” Well, sure, that's the way to bet: he was born in 1906 and while many people have lived longer, most don't. But how you can you be certain? I'd say, should an experiment for neutrinoless double beta decay prove conclusive, award him the prize and see if he shows up to accept it. Then we'll all know for sure.

Heck, if he did, it'd probably make Drudge.

December 2009 

Mahon, Basil. The Man Who Changed Everything. Chichester, UK: John Wiley & Sons, 2003. ISBN 978-0-470-86171-4.

In the 19th century, science in general and physics in particular grew up, assuming their modern form which is still recognisable today. At the start of the century, the word “scientist” was not yet in use, and the natural philosophers of the time were often amateurs. University research in the sciences, particularly in Britain, was rare. Those working in the sciences were often occupied by cataloguing natural phenomena, and apart from Newton's monumental achievements, few people focussed on discovering mathematical laws to explain the new physical phenomena which were being discovered such as electricity and magnetism.

One person, James Clerk Maxwell, was largely responsible for creating the way modern science is done and the way we think about theories of physics, while simultaneously restoring Britain's standing in physics compared to work on the Continent, and he created an institution which would continue to do important work from the time of his early death until the present day. While every physicist and electrical engineer knows of Maxwell and his work, he is largely unknown to the general public, and even those who are aware of his seminal work in electromagnetism may be unaware of the extent his footprints are found all over the edifice of 19th century physics.

Maxwell was born in 1831 to a Scottish lawyer, John Clerk, and his wife Frances Cay. Clerk subsequently inherited a country estate, and added “Maxwell” to his name in honour of the noble relatives from whom he inherited it. His son's first name, then was “James” and his surname “Clerk Maxwell”: this is why his full name is always used instead of “James Maxwell”. From childhood, James was curious about everything he encountered, and instead of asking “Why?” over and over like many children, he drove his parents to distraction with “What's the go o' that?”. His father did not consider science a suitable occupation for his son and tried to direct him toward the law, but James's curiosity did not extend to legal tomes and he concentrated on topics that interested him. He published his first scientific paper, on curves with more than two foci, at the age of 14. He pursued his scientific education first at the University of Edinburgh and later at Cambridge, where he graduated in 1854 with a degree in mathematics. He came in second in the prestigious Tripos examination, earning the title of Second Wrangler.

Maxwell was now free to begin his independent research, and he turned to the problem of human colour vision. It had been established that colour vision worked by detecting the mixture of three primary colours, but Maxwell was the first to discover that these primaries were red, green, and blue, and that by mixing them in the correct proportion, white would be produced. This was a matter to which Maxwell would return repeatedly during his life.

In 1856 he accepted an appointment as a full professor and department head at Marischal College, in Aberdeen Scotland. In 1857, the topic for the prestigious Adams Prize was the nature of the rings of Saturn. Maxwell's submission was a tour de force which proved that the rings could not be either solid nor a liquid, and hence had to be made of an enormous number of individually orbiting bodies. Maxwell was awarded the prize, the significance of which was magnified by the fact that his was the only submission: all of the others who aspired to solve the problem had abandoned it as too difficult.

Maxwell's next post was at King's College London, where he investigated the properties of gases and strengthened the evidence for the molecular theory of gases. It was here that he first undertook to explain the relationship between electricity and magnetism which had been discovered by Michael Faraday. Working in the old style of physics, he constructed an intricate mechanical thought experiment model which might explain the lines of force that Faraday had introduced but which many scientists thought were mystical mumbo-jumbo. Maxwell believed the alternative of action at a distance without any intermediate mechanism was wrong, and was able, with his model, to explain the phenomenon of rotation of the plane of polarisation of light by a magnetic field, which had been discovered by Faraday. While at King's College, to demonstrate his theory of colour vision, he took and displayed the first colour photograph.

Maxwell's greatest scientific achievement was done while living the life of a country gentleman at his estate, Glenair. In his textbook, A Treatise on Electricity and Magnetism, he presented his famous equations which showed that electricity and magnetism were two aspects of the same phenomenon. This was the first of the great unifications of physical laws which have continued to the present day. But that isn't all they showed. The speed of light appeared as a conversion factor between the units of electricity and magnetism, and the equations allowed solutions of waves oscillating between an electric and magnetic field which could propagate through empty space at the speed of light. It was compelling to deduce that light was just such an electromagnetic wave, and that waves of other frequencies outside the visual range must exist. Thus was laid the foundation of wireless communication, X-rays, and gamma rays. The speed of light is a constant in Maxwell's equations, not depending upon the motion of the observer. This appears to conflict with Newton's laws of mechanics, and it was not until Einstein's 1905 paper on special relativity that the mystery would be resolved. In essence, faced with a dispute between Newton and Maxwell, Einstein decided to bet on Maxwell, and he chose wisely. Finally, when you look at Maxwell's equations (in their modern form, using the notation of vector calculus), they appear lopsided. While they unify electricity and magnetism, the symmetry is imperfect in that while a moving electric charge generates a magnetic field, there is no magnetic charge which, when moved, generates an electric field. Such a charge would be a magnetic monopole, and despite extensive experimental searches, none has ever been found. The existence of monopoles would make Maxwell's equations even more beautiful, but sometimes nature doesn't care about that. By all evidence to date, Maxwell got it right.

In 1871 Maxwell came out of retirement to accept a professorship at Cambridge and found the Cavendish Laboratory, which would focus on experimental science and elevate Cambridge to world-class status in the field. To date, 29 Nobel Prizes have been awarded for work done at the Cavendish.

Maxwell's theoretical and experimental work on heat and gases revealed discrepancies which were not explained until the development of quantum theory in the 20th century. His suggestion of Maxwell's demon posed a deep puzzle in the foundations of thermodynamics which eventually, a century later, showed the deep connections between information theory and statistical mechanics. His practical work on automatic governors for steam engines foreshadowed what we now call control theory. He played a key part in the development of the units we use for electrical quantities.

By all accounts Maxwell was a modest, generous, and well-mannered man. He wrote whimsical poetry, discussed a multitude of topics (although he had little interest in politics), was an enthusiastic horseman and athlete (he would swim in the sea off Scotland in the winter), and was happily married, with his wife Katherine an active participant in his experiments. All his life, he supported general education in science, founding a working men's college in Cambridge and lecturing at such colleges throughout his career.

Maxwell lived only 48 years—he died in 1879 of the same cancer which had killed his mother when he was only eight years old. When he fell ill, he was engaged in a variety of research while presiding at the Cavendish Laboratory. We shall never know what he might have done had he been granted another two decades.

Apart from the significant achievements Maxwell made in a wide variety of fields, he changed the way physicists look at, describe, and think about natural phenomena. After using a mental model to explore electromagnetism, he discarded it in favour of a mathematical description of its behaviour. There is no theory behind Maxwell's equations: the equations are the theory. To the extent they produce the correct results when experimental conditions are plugged in, and predict new phenomena which are subsequently confirmed by experiment, they are valuable. If they err, they should be supplanted by something more precise. But they say nothing about what is really going on—they only seek to model what happens when you do experiments. Today, we are so accustomed to working with theories of this kind: quantum mechanics, special and general relativity, and the standard model of particle physics, that we don't think much about it, but it was revolutionary in Maxwell's time. His mathematical approach, like Newton's, eschewed explanation in favour of prediction: “We have no idea how it works, but here's what will happen if you do this experiment.” This is perhaps Maxwell's greatest legacy.

This is an excellent scientific biography of Maxwell which also gives the reader a sense of the man. He was such a quintessentially normal person there aren't a lot of amusing anecdotes to relate. He loved life, loved his work, cherished his friends, and discovered the scientific foundations of the technologies which allow you to read this. In the Kindle edition, at least as read on an iPad, the text appears in a curious, spidery, almost vintage, font in which periods are difficult to distinguish from commas. Numbers sometimes have spurious spaces embedded within them, and the index cites pages in the print edition which are useless since the Kindle edition does not include real page numbers.

August 2014 

Mahon, Basil. The Forgotten Genius of Oliver Heaviside. Amherst, NY: Prometheus Books, 2017. ISBN 978-1-63388-331-4.

At age eleven, in 1861, young Oliver Heaviside's family, supported by his father's irregular income as an engraver of woodblock illustrations for publications (an art beginning to be threatened by the advent of photography) and a day school for girls operated by his mother in the family's house, received a small legacy which allowed them to move to a better part of London and enroll Oliver in the prestigious Camden House School, where he ranked among the top of his class, taking thirteen subjects including Latin, English, mathematics, French, physics, and chemistry. His independent nature and iconoclastic views had already begun to manifest themselves: despite being an excellent student he dismissed the teaching of Euclid's geometry in mathematics and English rules of grammar as worthless. He believed that both mathematics and language were best learned, as he wrote decades later, “observationally, descriptively, and experimentally.” These principles would guide his career throughout his life.

At age fifteen he took the College of Perceptors examination, the equivalent of today's A Levels. He was the youngest of the 538 candidates to take the examination and scored fifth overall and first in the natural sciences. This would easily have qualified him for admission to university, but family finances ruled that out. He decided to study on his own at home for two years and then seek a job, perhaps in the burgeoning telegraph industry. He would receive no further formal education after the age of fifteen.

His mother's elder sister had married Charles Wheatstone, a successful and wealthy scientist, inventor, and entrepreneur whose inventions include the concertina, the stereoscope, and the Playfair encryption cipher, and who made major contributions to the development of telegraphy. Wheatstone took an interest in his bright nephew, and guided his self-studies after leaving school, encouraging him to master the Morse code and the German and Danish languages. Oliver's favourite destination was the library, which he later described as “a journey into strange lands to go a book-tasting”. He read the original works of Newton, Laplace, and other “stupendous names” and discovered that with sufficient diligence he could figure them out on his own.

At age eighteen, he took a job as an assistant to his older brother Arthur, well-established as a telegraph engineer in Newcastle. Shortly thereafter, probably on the recommendation of Wheatstone, he was hired by the just-formed Danish-Norwegian-English Telegraph Company as a telegraph operator at a salary of £150 per year (around £12000 in today's money). The company was about to inaugurate a cable under the North Sea between England and Denmark, and Oliver set off to Jutland to take up his new post. Long distance telegraphy via undersea cables was the technological frontier at the time—the first successful transatlantic cable had only gone into service two years earlier, and connecting the continents into a world-wide web of rapid information transfer was the booming high-technology industry of the age. While the job of telegraph operator might seem a routine clerical task, the élite who operated the undersea cables worked in an environment akin to an electrical research laboratory, trying to wring the best performance (words per minute) from the finicky and unreliable technology.

Heaviside prospered in the new job, and after a merger was promoted to chief operator at a salary of £175 per year and transferred back to England, at Newcastle. At the time, undersea cables were unreliable. It was not uncommon for the signal on a cable to fade and then die completely, most often due to a short circuit caused by failure of the gutta-percha insulation between the copper conductor and the iron sheath surrounding it. When a cable failed, there was no alternative but to send out a ship which would find the cable with a grappling hook, haul it up to the surface, cut it, and test whether the short was to the east or west of the ship's position (the cable would work in the good direction but fail in that containing the short. Then the cable would be re-spliced, dropped back to the bottom, and the ship would set off in the direction of the short to repeat the exercise over and over until, by a process similar to binary search, the location of the fault was narrowed down and that section of the cable replaced. This was time consuming and potentially hazardous given the North Sea's propensity for storms, and while the cable remained out of service it made no money for the telegraph company.

Heaviside, who continued his self-study and frequented the library when not at work, realised that knowing the resistance and length of the functioning cable, which could be easily measured, it would be possible to estimate the location of the short simply by measuring the resistance of the cable from each end after the short appeared. He was able to cancel out the resistance of the fault, creating a quadratic equation which could be solved for its location. The first time he applied this technique his bosses were sceptical, but when the ship was sent out to the location he predicted, 114 miles from the English coast, they quickly found the short circuit.

At the time, most workers in electricity had little use for mathematics: their trade journal, The Electrician (which would later publish much of Heaviside's work) wrote in 1861, “In electricity there is seldom any need of mathematical or other abstractions; and although the use of formulæ may in some instances be a convenience, they may for all practical purpose be dispensed with.” Heaviside demurred: while sharing disdain for abstraction for its own sake, he valued mathematics as a powerful tool to understand the behaviour of electricity and attack problems of great practical importance, such as the ability to send multiple messages at once on the same telegraphic line and increase the transmission speed on long undersea cable links (while a skilled telegraph operator could send traffic at thirty words per minute on intercity land lines, the transatlantic cable could run no faster than eight words per minute). He plunged into calculus and differential equations, adding them to his intellectual armamentarium.

He began his own investigations and experiments and began to publish his results, first in English Mechanic, and then, in 1873, the prestigious Philosophical Magazine, where his work drew the attention of two of the most eminent workers in electricity: William Thomson (later Lord Kelvin) and James Clerk Maxwell. Maxwell would go on to cite Heaviside's paper on the Wheatstone Bridge in the second edition of his Treatise on Electricity and Magnetism, the foundation of the classical theory of electromagnetism, considered by many the greatest work of science since Newton's Principia, and still in print today. Heady stuff, indeed, for a twenty-two year old telegraph operator who had never set foot inside an institution of higher education.

Heaviside regarded Maxwell's Treatise as the path to understanding the mysteries of electricity he encountered in his practical work and vowed to master it. It would take him nine years and change his life. He would become one of the first and foremost of the “Maxwellians”, a small group including Heaviside, George FitzGerald, Heinrich Hertz, and Oliver Lodge, who fully grasped Maxwell's abstract and highly mathematical theory (which, like many subsequent milestones in theoretical physics, predicted the results of experiments without providing a mechanism to explain them, such as earlier concepts like an “electric fluid” or William Thomson's intricate mechanical models of the “luminiferous ether”) and built upon its foundations to discover and explain phenomena unknown to Maxwell (who would die in 1879 at the age of just 48).

While pursuing his theoretical explorations and publishing papers, Heaviside tackled some of the main practical problems in telegraphy. Foremost among these was “duplex telegraphy”: sending messages in each direction simultaneously on a single telegraph wire. He invented a new technique and was even able to send two messages at the same time in both directions as fast as the operators could send them. This had the potential to boost the revenue from a single installed line by a factor of four. Oliver published his invention, and in doing so made an enemy of William Preece, a senior engineer at the Post Office telegraph department, who had invented and previously published his own duplex system (which would not work), that was not acknowledged in Heaviside's paper. This would start a feud between Heaviside and Preece which would last the rest of their lives and, on several occasions, thwart Heaviside's ambition to have his work accepted by mainstream researchers. When he applied to join the Society of Telegraph Engineers, he was rejected on the grounds that membership was not open to “clerks”. He saw the hand of Preece and his cronies at the Post Office behind this and eventually turned to William Thomson to back his membership, which was finally granted.

By 1874, telegraphy had become a big business and the work was increasingly routine. In 1870, the Post Office had taken over all domestic telegraph service in Britain and, as government is wont to do, largely stifled innovation and experimentation. Even at privately-owned international carriers like Oliver's employer, operators were no longer concerned with the technical aspects of the work but rather tending automated sending and receiving equipment. There was little interest in the kind of work Oliver wanted to do: exploring the new horizons opened up by Maxwell's work. He decided it was time to move on. So, he quit his job, moved back in with his parents in London, and opted for a life as an independent, unaffiliated researcher, supporting himself purely by payments for his publications.

With the duplex problem solved, the largest problem that remained for telegraphy was the slow transmission speed on long lines, especially submarine cables. The advent of the telephone in the 1870s would increase the need to address this problem. While telegraphic transmission on a long line slowed down the speed at which a message could be sent, with the telephone voice became increasingly distorted the longer the line, to the point where, after around 100 miles, it was incomprehensible. Until this was understood and a solution found, telephone service would be restricted to local areas.

Many of the early workers in electricity thought of it as something like a fluid, where current flowed through a wire like water through a pipe. This approximation is more or less correct when current flow is constant, as in a direct current generator powering electric lights, but when current is varying a much more complex set of phenomena become manifest which require Maxwell's theory to fully describe. Pioneers of telegraphy thought of their wires as sending direct current which was simply switched off and on by the sender's key, but of course the transmission as a whole was a varying current, jumping back and forth between zero and full current at each make or break of the key contacts. When these transitions are modelled in Maxwell's theory, one finds that, depending upon the physical properties of the transmission line (its resistance, inductance, capacitance, and leakage between the conductors) different frequencies propagate along the line at different speeds. The sharp on/off transitions in telegraphy can be thought of, by Fourier transform, as the sum of a wide band of frequencies, with the result that, when each propagates at a different speed, a short, sharp pulse sent by the key will, at the other end of the long line, be “smeared out” into an extended bump with a slow rise to a peak and then decay back to zero. Above a certain speed, adjacent dots and dashes will run into one another and the message will be undecipherable at the receiving end. This is why operators on the transatlantic cables had to send at the painfully slow speed of eight words per minute.

In telephony, it's much worse because human speech is composed of a broad band of frequencies, and the frequencies involved (typically up to around 3400 cycles per second) are much higher than the off/on speeds in telegraphy. The smearing out or dispersion as frequencies are transmitted at different speeds results in distortion which renders the voice signal incomprehensible beyond a certain distance.

In the mid-1850s, during development of the first transatlantic cable, William Thomson had developed a theory called the “KR law” which predicted the transmission speed along a cable based upon its resistance and capacitance. Thomson was aware that other effects existed, but without Maxwell's theory (which would not be published in its final form until 1873), he lacked the mathematical tools to analyse them. The KR theory, which produced results that predicted the behaviour of the transatlantic cable reasonably well, held out little hope for improvement: decreasing the resistance and capacitance of the cable would dramatically increase its cost per unit length.

Heaviside undertook to analyse what is now called the transmission line problem using the full Maxwell theory and, in 1878, published the general theory of propagation of alternating current through transmission lines, what are now called the telegrapher's equations. Because he took resistance, capacitance, inductance, and leakage all into account and thus modelled both the electric and magnetic field created around the wire by the changing current, he showed that by balancing these four properties it was possible to design a transmission line which would transmit all frequencies at the same speed. In other words, this balanced transmission line would behave for alternating current (including the range of frequencies in a voice signal) just like a simple wire did for direct current: the signal would be attenuated (reduced in amplitude) with distance but not distorted.

In an 1887 paper, he further showed that existing telegraph and telephone lines could be made nearly distortionless by adding loading coils to increase the inductance at points along the line (as long as the distance between adjacent coils is small compared to the wavelength of the highest frequency carried by the line). This got him into another battle with William Preece, whose incorrect theory attributed distortion to inductance and advocated minimising self-inductance in long lines. Preece moved to block publication of Heaviside's work, with the result that the paper on distortionless telephony, published in The Electrician, was largely ignored. It was not until 1897 that AT&T in the United States commissioned a study of Heaviside's work, leading to patents eventually worth millions. The credit, and financial reward, went to Professor Michael Pupin of Columbia University, who became another of Heaviside's life-long enemies.

You might wonder why what seems such a simple result (which can be written in modern notation as the equation L/R = C/G) which had such immediate technological utlilty eluded so many people for so long (recall that the problem with slow transmission on the transatlantic cable had been observed since the 1850s). The reason is the complexity of Maxwell's theory and the formidably difficult notation in which it was expressed. Oliver Heaviside spent nine years fully internalising the theory and its implications, and he was one of only a handful of people who had done so and, perhaps, the only one grounded in practical applications such as telegraphy and telephony. Concurrent with his work on transmission line theory, he invented the mathematical field of vector calculus and, in 1884, reformulated Maxwell's original theory which, written in modern notation less cumbersome than that employed by Maxwell, looks like:

into the four famous vector equations we today think of as Maxwell's.

These are not only simpler, condensing twenty equations to just four, but provide (once you learn the notation and meanings of the variables) an intuitive sense for what is going on. This made, for the first time, Maxwell's theory accessible to working physicists and engineers interested in getting the answer out rather than spending years studying an arcane theory. (Vector calculus was independently invented at the same time by the American J. Willard Gibbs. Heaviside and Gibbs both acknowledged the work of the other and there was no priority dispute. The notation we use today is that of Gibbs, but the mathematical content of the two formulations is essentially identical.)

And, during the same decade of the 1880s, Heaviside invented the operational calculus, a method of calculation which reduces the solution of complicated problems involving differential equations to simple algebra. Heaviside was able to solve so many problems which others couldn't because he was using powerful computational tools they had not yet adopted. The situation was similar to that of Isaac Newton who was effortlessly solving problems such as the brachistochrone using the calculus he'd invented while his contemporaries struggled with more cumbersome methods. Some of the things Heaviside did in the operational calculus, such as cancel derivative signs in equations and take the square root of a derivative sign made rigorous mathematicians shudder but, hey, it worked and that was good enough for Heaviside and the many engineers and applied mathematicians who adopted his methods. (In the 1920s, pure mathematicians used the theory of Laplace transforms to reformulate the operational calculus in a rigorous manner, but this was decades after Heaviside's work and long after engineers were routinely using it in their calculations.)

Heaviside's intuitive grasp of electromagnetism and powerful computational techniques placed him in the forefront of exploration of the field. He calculated the electric field of a moving charged particle and found it contracted in the direction of motion, foreshadowing the Lorentz-FitzGerald contraction which would figure in Einstein's special relativity. In 1889 he computed the force on a point charge moving in an electromagnetic field, which is now called the Lorentz force after Hendrik Lorentz who independently discovered it six years later. He predicted that a charge moving faster than the speed of light in a medium (for example, glass or water) would emit a shock wave of electromagnetic radiation; in 1934 Pavel Cherenkov experimentally discovered the phenomenon, now called Cherenkov radiation, for which he won the Nobel Prize in 1958. In 1902, Heaviside applied his theory of transmission lines to the Earth as a whole and explained the propagation of radio waves over intercontinental distances as due to a transmission line formed by conductive seawater and a hypothetical conductive layer in the upper atmosphere dubbed the Heaviside layer. In 1924 Edward V. Appleton confirmed the existence of such a layer, the ionosphere, and won the Nobel prize in 1947 for the discovery.

Oliver Heaviside never won a Nobel Price, although he was nominated for the physics prize in 1912. He shouldn't have felt too bad, though, as other nominees passed over for the prize that year included Hendrik Lorentz, Ernst Mach, Max Planck, and Albert Einstein. (The winner that year was Gustaf Dalén, “for his invention of automatic regulators for use in conjunction with gas accumulators for illuminating lighthouses and buoys”—oh well.) He did receive Britain's highest recognition for scientific achievement, being named a Fellow of the Royal Society in 1891. In 1921 he was the first recipient of the Faraday Medal from the Institution of Electrical Engineers.

Having never held a job between 1874 and his death in 1925, Heaviside lived on his irregular income from writing, the generosity of his family, and, from 1896 onward a pension of £120 per year (less than his starting salary as a telegraph operator in 1868) from the Royal Society. He was a proud man and refused several other offers of money which he perceived as charity. He turned down an offer of compensation for his invention of loading coils from AT&T when they refused to acknowledge his sole responsibility for the invention. He never married, and in his elder years became somewhat of a recluse and, although he welcomed visits from other scientists, hardly ever left his home in Torquay in Devon.

His impact on the physics of electromagnetism and the craft of electrical engineering can be seen in the list of terms he coined which are in everyday use: “admittance”, “conductance”, “electret”, “impedance”, “inductance”, “permeability”, “permittance”, “reluctance”, and “susceptance”. His work has never been out of print, and sparkles with his intuition, mathematical prowess, and wicked wit directed at those he considered pompous or lost in needless abstraction and rigor. He never sought the limelight and among those upon whose work much of our present-day technology is founded, he is among the least known. But as long as electronic technology persists, it is a monument to the life and work of Oliver Heaviside.

November 2018 

Moffat, John W. Reinventing Gravity. New York: Collins, 2008. ISBN 978-0-06-117088-1.

In the latter half of the nineteenth century, astronomers were confronted by a puzzling conflict between their increasingly precise observations and the predictions of Newton's time-tested theory of gravity. The perihelion of the elliptical orbit of the planet Mercury was found to precess by the tiny amount of 43 arc seconds per century more than could be accounted for by the gravitational influence of the Sun and the other planets. While small, the effect was unambiguously measured, and indicated that something was missing in the analysis. Urbain Le Verrier, coming off his successful prediction of the subsequently discovered planet Neptune by analysis of the orbit of Uranus, calculated that Mercury's anomalous precession could be explained by the presence of a yet unobserved planet he dubbed Vulcan. Astronomers set out to observe the elusive inner planet in transit across the Sun or during solar eclipses, and despite several sightings by respectable observers, no confirmed observations were made. Other astronomers suggested a belt of asteroids too small to observe within the orbit of Mercury could explain its orbital precession. For more than fifty years, dark matter—gravitating body or bodies so far unobserved—was invoked to explain a discrepancy between the regnant theory of gravitation and the observations of astronomers. Then, in 1915, Einstein published his General Theory of Relativity which predicted that orbits in strongly curved spacetime would precess precisely the way Mercury's orbit was observed to, and that no dark matter was needed to reconcile the theory of gravitation with observations. So much for planet Vulcan, notwithstanding the subsequent one with all the pointy-eared logicians.

In the second half of the twentieth century, a disparate collection of observations on the galactic scale and beyond: the speed of rotation of stars in the discs of spiral galaxies, the velocities of galaxies in galactic clusters, gravitational lensing of distant objects by foreground galaxy clusters, the apparent acceleration of the expansion of the universe, and the power spectrum of the anisotropies in the cosmic background radiation, have yielded results grossly at variance with the predictions of General Relativity. The only way to make the results fit the theory is to assume that everything we observe in the cosmos makes up less than 5% of its total mass, and that the balance is “dark matter” and “dark energy”, neither of which has yet been observed or detected apart from their imputed gravitational effects. Sound familiar?

In this book, John Moffat, a distinguished physicist who has spent most of his long career exploring extensions to Einstein's theory of General Relativity, dares to suggest that history may be about to repeat itself, and that the discrepancy between what our theories predict and what we observe may not be due to something we haven't seen, but rather limitations in the scope of validity of our theories. Just as Newton's theory of gravity, exquisitely precise on the terrestrial scale and in the outer solar system, failed when applied to the strong gravitational field close to the Sun in which Mercury orbits, perhaps Einstein's theory also requires corrections over the very large distances involved in the galactic and cosmological scales. The author recounts his quest for such a theory, and eventual development of Modified Gravity (MOG), a scalar/tensor/vector field theory which reduces to Einstein's General Relativity when the scalar and vector fields are set to zero.

This theory is claimed to explain all of these large scale discrepancies without invoking dark matter, and to do so, after calibration of the static fields from observational data, with no free parameters (“fudge factors”). Unlike some other speculative theories, MOG makes a number of predictions which it should be possible to test in the next decade. MOG predicts a very different universe in the strong field regime than General Relativity: there are no black holes, no singularities, and the Big Bang is replaced by a universe which starts out with zero matter density and zero entropy at the start and decays because, as we all know, nothing is unstable.

The book is fascinating, but in a way unsatisfying. The mathematical essence of the theory is never explained: you'll have to read the author's professional publications to find it. There are no equations, not even in the end notes, which nonetheless contain prose such as (p. 235):

Wilson loops can describe a gauge theory such as Maxwell's theory of electromagnetism or the gauge theory of the standard model of particle physics. These loops are gauge-invariant observables obtained from the holonomy of the gauge connection around a given loop. The holonomy of a connection in differential geometry on a smooth manifold is defined as the measure to which parallel transport around closed loops fails to preserve the geometrical data being transported. Holonomy has nontrivial local and global features for curved connections.

I know that they say you lose half the audience for every equation you include in a popular science book, but this is pretty forbidding stuff for anybody who wanders into the notes. For a theory like this, the fit to the best available observational data is everything, and this is discussed almost everywhere only in qualitative terms. Let's see the numbers! Although there is a chapter on string theory and quantum gravity, these topics are dropped in the latter half of the book: MOG is a purely classical theory, and there is no discussion of how it might lead toward the quantisation of gravitation or be an emergent effective field theory of a lower level quantum substrate.

There aren't many people with the intellect, dogged persistence, and self-confidence to set out on the road to deepen our understanding of the universe at levels far removed from those of our own experience. Einstein struggled for ten years getting from Special to General Relativity, and Moffat has worked for three times as long arriving at MOG and working out its implications. If it proves correct, it will be seen as one of the greatest intellectual achievements by a single person (with a small group of collaborators) in recent history. Should that be the case (and several critical tests which may knock the theory out of the box will come in the near future), this book will prove a unique look into how the theory was so patiently constructed. It's amusing to reflect, if it turns out that dark matter and dark energy end up being epicycles invoked to avoid questioning a theory never tested in the domains in which it was being applied, how historians of science will look back at our age and wryly ask, “What were they thinking?”.

I have a photo credit on p. 119 for a vegetable.

April 2009 

Pais, Abraham. The Genius of Science. Oxford: Oxford University Press, 2000. ISBN 0-19-850614-7.

In this volume Abraham Pais, distinguished physicist and author of Subtle Is the Lord, the definitive scientific biography of Einstein, presents a “portrait gallery” of eminent twentieth century physicists, including Bohr, Dirac, Pauli, von Neumann, Rabi, and others. If you skip the introduction, you may be puzzled at some of the omissions: Heisenberg, Fermi, and Feynman, among others. Pais wanted to look behind the physics to the physicist, and thus restricted his biographies to scientists he personally knew; those not included simply didn't cross his career path sufficiently to permit sketching them in adequate detail. Many of the chapters were originally written for publication in other venues and revised for this book; consequently the balance of scientific and personal biography varies substantially among them, as does the length of the pieces: the chapter on Victor Weisskopf, adapted from an honorary degree presentation, is a mere two and half pages, while that on George Eugene Uhlenbeck, based on a lecture from a memorial symposium, is 33 pages long. The scientific focus is very much on quantum theory and particle physics, and the collected biographies provide an excellent view of the extent to which researchers groped in the dark before discovering phenomena which, presented in a modern textbook, seem obvious in retrospect. One wonders whether the mysteries of present-day physics will seem as straightforward a century from now.

April 2005 

Penrose, Roger. The Road to Reality. New York: Alfred A. Knopf, 2005. ISBN 0-679-45443-8.

This is simply a monumental piece of work. I can't think of any comparable book published in the last century, or any work with such an ambitious goal which pulls it off so well. In this book, Roger Penrose presents the essentials of fundamental physics as understood at the turn of the century to the intelligent layman in the way working theoretical physicists comprehend them. Starting with the Pythagorean theorem, the reader climbs the ladder of mathematical abstraction to master complex numbers, logarithms, real and complex number calculus, Fourier decomposition, hyperfunctions, quaternions and octionions, manifolds and calculus on manifolds, symmetry groups, fibre bundles and connections, transfinite numbers, spacetime, Hamiltonians and Lagrangians, Clifford and Grassman algebras, tensor calculus, and the rest of the mathematical armamentarium of the theoretical physicist. And that's before we get to the physics, where classical mechanics and electrodynamics, special and general relativity, quantum mechanics, and the standard models of particle physics and cosmology are presented in the elegant and economical notation into which the reader has been initiated in the earlier chapters.

Authors of popular science books are cautioned that each equation they include (except, perhaps E=mc²) will halve the sales of their book. Penrose laughs in the face of such fears. In this “big damned fat square book” of 1050 pages of main text, there's an average of one equation per page, which, according to conventional wisdom should reduce readership by a factor of 2⁻¹⁰⁵⁰ or 8.3×10⁻³¹⁷, so the single copy printed would have to be shared by among the 10⁸⁰ elementary particles in the universe over an extremely long time. But, according to the Amazon sales ranking as of today, this book is number 71 in sales—go figure.

Don't deceive yourself; in committing to read this book you are making a substantial investment of time and brain power to master the underlying mathematical concepts and their application to physical theories. If you've noticed my reading being lighter than usual recently, both in terms of number of books and their intellectual level, it's because I've been chewing through this tome for last two and a half months and it's occupied my cerebral capacity to the exclusion of other works. But I do not regret for a second the time I've spent reading this work and working the exercises, and I will probably make a second pass through it in a couple of years to reinforce the mathematical toolset into my aging neurons. As an engineer whose formal instruction in mathematics ended with differential equations, I found chapters 12–15 to be the “hump”—after making it through them (assuming you've mastered their content), the rest of the book is much more physical and accessible. There's kind of a phase transition between the first part of the book and chapters 28–34. In the latter part of the book, Penrose gives free rein to his own view of fundamental physics, introducing his objective reduction of the quantum state function (OR) by gravity, twistor theory, and a deconstruction of string theory which may induce apoplexy in researchers engaged in that programme. But when discussing speculative theories, he takes pains to identify his own view when it differs from the consensus, and to caution the reader where his own scepticism is at variance with a widely accepted theory (such as cosmological inflation).

If you really want to understand contemporary physics at the level of professional practitioners, I cannot recommend this book too highly. After you've mastered this material, you should be able to read research reports in the General Relativity and Quantum Cosmology preprint archives like the folks who write and read them. Imagine if, instead of two or three hundred taxpayer funded specialists, four or five thousand self-educated people impassioned with figuring out how nature does it contributed every day to our unscrewing of the inscrutable. Why, they'll say it's a movement. And that's exactly what it will be.

March 2005 

Penrose, Roger. Cycles of Time. New York: Alfred A. Knopf, 2010. ISBN 978-0-307-26590-6.

One of the greatest and least appreciated mysteries of contemporary cosmology is the extraordinarily special state of the universe immediately after the big bang. While at first glance an extremely hot and dense mass of elementary particles and radiation near thermal equilibrium might seem to have near-maximum entropy, when gravitation is taken into account, its homogeneity (the absence of all but the most tiny fluctuations in density) actually caused it to have a very small entropy. Only a universe which began in such a state could have a well-defined arrow of time which permits entropy to steadily increase over billions of years as dark matter and gas clump together, stars and galaxies form, and black holes appear and swallow up matter and radiation. If the process of the big bang had excited gravitational degrees of freedom, the overwhelmingly most probable outcome would be a mess of black holes with a broad spectrum of masses, which would evolve into a universe which looks nothing like the one we inhabit. As the author has indefatigably pointed out for many years, for some reason the big bang produced a universe in what appears to be an extremely improbable state. Why is this? (The preceding sketch may be a bit telegraphic because I discussed these issues at much greater length in my review of Sean Carroll's From Eternity to Here [February 2010] and didn't want to repeat it all here. So, if you aren't sure what I just said, you may wish to read that review before going further.)

In this book, Penrose proposes “conformal cyclic cosmology” as the solution to this enigma. Let's pick this apart, word by word. A conformal transformation is a mathematical mapping which preserves angles in infinitesimal figures. It is possible to define a conformal transformation (for example, the hyperbolic transformation illustrated by M. C. Escher's Circle Limit III) which maps an infinite space onto a finite one. The author's own Penrose diagrams map all of (dimension reduced) space-time onto a finite plot via a conformal transformation. Penrose proposes a conformal transformation which maps the distant future of a dead universe undergoing runaway expansion to infinity with the big bang of a successor universe, resulting in a cyclic history consisting of an infinite number of “æons”, each beginning with its own big bang and ending in expansion to infinity. The resulting cosmology is that of a single universe evolving from cycle to cycle, with the end of each cycle producing the seemingly improbable conditions required at the start of the next. There is no need for an inflationary epoch after the big bang, a multitude of unobservable universes in a “multiverse”, or invoking the anthropic principle to explain the apparent fine-tuning of the big bang—in Penrose's cosmology, the physics makes those conditions inevitable.

Now, the conformal rescaling Penrose invokes only works if the universe contains no massive particles, as only massless particles which always travel at the speed of light are invariant under the conformal transformation. Hence for the scheme to work, there must be only massless particles in the universe at the end of the previous æon and immediately after the big bang—the moment dubbed the “crossover”. Penrose argues that at the enormous energies immediately after the big bang, all particles were effectively massless anyway, with mass emerging only through symmetry breaking as the universe expanded and cooled. On the other side of the crossover, he contends that in the distant future of the previous æon almost all mass will have been accreted by black holes which then will evaporate through the Hawking process into particles which will annihilate, yielding a universe containing only massless photons and gravitons. He does acknowledge that some matter may escape the black holes, but then proposes (rather dubiously in my opinion) that all stable massive particles are ultimately unstable on this vast time scale (a hundred orders of magnitude longer than the time since the big bang), or that mass may just “fade away” as the universe ages: kind of like the Higgs particle getting tired (but then most of the mass of stable hadrons doesn't come from the Higgs process, but rather the internal motion of their component quarks and gluons).

Further, Penrose believes that information is lost when it falls to the singularity within a black hole, and is not preserved in some correlation at the event horizon or in the particles emitted as the black hole evaporates. (In this view he is now in a distinct minority of theoretical physicists.) This makes black holes into entropy destroying machines. They devour all of the degrees of freedom of the particles that fall into them and then, when they evaporate with a “pop”, it's all lost and gone away. This allows Penrose to avoid what would otherwise be a gross violation of the second law of thermodynamics. In his scheme the big bang has very low entropy because all of the entropy created in the prior æon has been destroyed by falling into black holes which subsequently evaporate.

All of this is very original, clever, and the mathematics is quite beautiful, but it's nothing more than philosophical speculation unless it makes predictions which can be tested by observation or experiment. Penrose believes that gravitational radiation emitted from the violent merger of galactic-mass black holes in the previous æon may come through the crossover and imprint itself as concentric circles of low temperature variation in the cosmic background radiation we observe today. Further, with a colleague, he argues that precisely such structures have been observed in two separate surveys of the background radiation. Other researchers dispute this claim, and the debate continues.

For the life of me, I cannot figure out to which audience this book is addressed. It starts out discussing the second law of thermodynamics and entropy in language you'd expect in a popularisation aimed at the general public, but before long we're into territory like:

We now ask for the analogues of F and J in the case of the gravitational field, as described by Einstein's general theory of relativity. In this theory there is a curvature to space-time (which can be calculated once knows how the metric g varies throughout the space-time), described by a [ ⁰₄]-tensor R, called the Riemann(-Christoffel) tensor, with somewhat complicated symmetries resulting in R having 20 independent components per point. These components can be separated into two parts, constituting a [ ⁰₄]-tensor C, with 10 independent components, called the Weyl conformal tensor, and a symmetric [ ⁰₂]-tensor E, also with 10 independent components, called the Einstein tensor (this being equivalent to a slightly different [ ⁰₂]-tensor referred to as the Ricci tensor^[2.57]). According to Einstein's field equations, it is E that provides the source to the gravitational field. (p. 129)

Ahhhh…now I understand! Seriously, much of this book is tough going, as technical in some sections as scholarly publications in the field of general relativity, and readers expecting a popular account of Penrose's proposal may not make it to the payoff at the end. For those who thirst for even more rigour there are two breathtakingly forbidding appendices.

The Kindle edition is excellent, with the table of contents, notes, cross-references, and index linked just as they should be.

October 2011 

Penrose, Roger. Fashion, Faith, and Fantasy. Princeton: Princeton University Press, 2016. ISBN 978-0-691-11979-3.

Sir Roger Penrose is one of the most distinguished theoretical physicists and mathematicians working today. He is known for his work on general relativity, including the Penrose-Hawking Singularity Theorems, which were a central part of the renaissance of general relativity and the acceptance of the physical reality of black holes in the 1960s and 1970s. Penrose has contributed to cosmology, argued that consciousness is not a computational process, speculated that quantum mechanical processes are involved in consciousness, proposed experimental tests to determine whether gravitation is involved in the apparent mysteries of quantum mechanics, explored the extraordinarily special conditions which appear to have obtained at the time of the Big Bang and suggested a model which might explain them, and, in mathematics, discovered Penrose tiling, a non-periodic tessellation of the plane which exhibits five-fold symmetry, which was used (without his permission) in the design of toilet paper.

“Fashion, Faith, and Fantasy” seems an odd title for a book about the fundamental physics of the universe by one of the most eminent researchers in the field. But, as the author describes in mathematical detail (which some readers may find forbidding), these all-too-human characteristics play a part in what researchers may present to the public as a dispassionate, entirely rational, search for truth, unsullied by such enthusiasms. While researchers in fundamental physics are rarely blinded to experimental evidence by fashion, faith, and fantasy, their choice of areas to explore, willingness to pursue intellectual topics far from any mooring in experiment, tendency to indulge in flights of theoretical fancy (for which there is no direct evidence whatsoever and which may not be possible to test, even in principle) do, the author contends, affect the direction of research, to its detriment.

To illustrate the power of fashion, Penrose discusses string theory, which has occupied the attentions of theorists for four decades and been described by some of its practitioners as “the only game in town”. (This is a piñata which has been whacked by others, including Peter Woit in Not Even Wrong [June 2006] and Lee Smolin in The Trouble with Physics [September 2006].) Unlike other critiques, which concentrate mostly on the failure of string theory to produce a single testable prediction, and the failure of experimentalists to find any evidence supporting its claims (for example, the existence of supersymmetric particles), Penrose concentrates on what he argues is a mathematical flaw in the foundations of string theory, which those pursuing it sweep under the rug, assuming that when a final theory is formulated (when?), its solution will be evident. Central to Penrose's argument is that string theories are formulated in a space with more dimensions than the three we perceive ourselves to inhabit. Depending upon the version of string theory, it may invoke 10, 11, or 26 dimensions. Why don't we observe these extra dimensions? Well, the string theorists argue that they're all rolled up into a size so tiny that none of our experiments can detect any of their effects. To which Penrose responds, “not so fast”: these extra dimensions, however many, will vastly increase the functional freedom of the theory and lead to a mathematical instability which will cause the theory to blow up much like the ultraviolet catastrophe which was a key motivation for the creation of the original version of quantum theory. String theorists put forward arguments why quantum effects may similarly avoid the catastrophe Penrose describes, but he dismisses them as no more than arm waving. If you want to understand the functional freedom argument in detail, you're just going to have to read the book. Explaining it here would require a ten kiloword review, so I shall not attempt it.

As an example of faith, Penrose cites quantum mechanics (and its extension, compatible with special relativity, quantum field theory), and in particular the notion that the theory applies to all interactions in the universe (excepting gravitation), regardless of scale. Quantum mechanics is a towering achievement of twentieth century physics, and no theory has been tested in so many ways over so many years, without the discovery of the slightest discrepancy between its predictions and experimental results. But all of these tests have been in the world of the very small: from subatomic particles to molecules of modest size. Quantum theory, however, prescribes no limit on the scale of systems to which it is applicable. Taking it to its logical limit, we arrive at apparent absurdities such as Schrödinger's cat, which is both alive and dead until somebody opens the box and looks inside. This then leads to further speculations such as the many-worlds interpretation, where the universe splits every time a quantum event happens, with every possible outcome occurring in a multitude of parallel universes.

Penrose suggests we take a deep breath, step back, and look at what's going on in quantum mechanics at the mathematical level. We have two very different processes: one, which he calls U, is the linear evolution of the wave function “when nobody's looking”. The other is R, the reduction of the wave function into one of a number of discrete states when a measurement is made. What's a measurement? Well, there's another ten thousand papers to read. The author suggests that extrapolating a theory of the very small (only tested on tiny objects under very special conditions) to cats, human observers, planets, and the universe, is an unwarranted leap of faith. Sure, quantum mechanics makes exquisitely precise predictions confirmed by experiment, but why should we assume it is correct when applied to domains which are dozens of orders of magnitude larger and more complicated? It's not physics, but faith.

Finally we come to cosmology: the origin of the universe we inhabit, and in particular the theory of the big bang and cosmic inflation, which Penrose considers an example of fantasy. Again, he turns to the mathematical underpinnings of the theory. Why is there an arrow of time? Why, if all of the laws of microscopic physics are reversible in time, can we so easily detect when a film of some real-world process (for example, scrambling an egg) is run backward? He argues (with mathematical rigour I shall gloss over here) that this is due to the extraordinarily improbable state in which our universe began at the time of the big bang. While the cosmic background radiation appears to be thermalised and thus in a state of very high entropy, the smoothness of the radiation (uniformity of temperature, which corresponds to a uniform distribution of mass-energy) is, when gravity is taken into account, a state of very low entropy which is the starting point that explains the arrow of time we observe.

When the first precision measurements of the background radiation were made, several deep mysteries became immediately apparent. How could regions which, given their observed separation on the sky and the finite speed of light, have arrived at such a uniform temperature? Why was the global curvature of the universe so close to flat? (If you run time backward, this appeared to require a fine-tuning of mind-boggling precision in the early universe.) And finally, why weren't there primordial magnetic monopoles everywhere? The most commonly accepted view is that these problems are resolved by cosmic inflation: a process which occurred just after the moment of creation and before what we usually call the big bang, which expanded the universe by a breathtaking factor and, by that expansion, smoothed out any irregularities in the initial state of the universe and yielded the uniformity we observe wherever we look. Again: “not so fast.”

As Penrose describes, inflation (which he finds dubious due to the lack of a plausible theory of what caused it and resulted in the state we observe today) explains what we observe in the cosmic background radiation, but it does nothing to solve the mystery of why the distribution of mass-energy in the universe was so uniform or, in other words, why the gravitational degrees of freedom in the universe were not excited. He then goes on to examine what he argues are even more fantastic theories including an infinite number of parallel universes, forever beyond our ability to observe.

In a final chapter, Penrose presents his own speculations on how fashion, faith, and fantasy might be replaced by physics: theories which, although they may be completely wrong, can at least be tested in the foreseeable future and discarded if they disagree with experiment or investigated further if not excluded by the results. He suggests that a small effort investigating twistor theory might be a prudent hedge against the fashionable pursuit of string theory, that experimental tests of objective reduction of the wave function due to gravitational effects be investigated as an alternative to the faith that quantum mechanics applies at all scales, and that his conformal cyclic cosmology might provide clues to the special conditions at the big bang which the fantasy of inflation theory cannot. (Penrose's cosmological theory is discussed in detail in Cycles of Time [October 2011]). Eleven mathematical appendices provide an introduction to concepts used in the main text which may be unfamiliar to some readers.

A special treat is the author's hand-drawn illustrations. In addition to being a mathematician, physicist, and master of scientific explanation and the English language, he is an inspired artist.

The Kindle edition is excellent, with the table of contents, notes, cross-references, and index linked just as they should be.

October 2016 

Pickover, Clifford A. Surfing through Hyperspace. Oxford: Oxford University Press, 1999. ISBN 0-19-514241-1.

October 2001 

Pickover, Clifford A. Black Holes: A Traveler's Guide. New York: John Wiley & Sons, 1998. ISBN 0-471-19704-1.

October 2001 

Pickover, Clifford A. Time: A Traveler's Guide. Oxford: Oxford University Press, 1998. ISBN 0-19-513096-0.

May 2002 

Randall, Lisa. Warped Passages. New York: Ecco, 2005. ISBN 0-06-053108-8.

The author is one of most prominent theoretical physicists working today, known primarily for her work on multi-dimensional “braneworld” models for particle physics and gravitation. With Raman Sundrum, she created the Randall-Sundrum models, the papers describing which are among the most highly cited in contemporary physics. In this book, aimed at a popular audience, she explores the revolution in theoretical physics which extra dimensional models have sparked since 1999, finally uniting string theorists, model builders, and experimenters in the expectation of finding signatures of new physics when the Large Hadron Collider (LHC) comes on stream at CERN in 2007.

The excitement among physicists is palpable: there is now reason to believe that the unification of all the forces of physics, including gravity, may not lie forever out of reach at the Planck energy, but somewhere in the TeV range—which will be accessible at the LHC. This book attempts to communicate that excitement to the intelligent layman and, sadly, falls somewhat short of the mark. The problem, in a nutshell, is that while the author is a formidable physicist, she is not, at least at this point in her career, a particularly talented populariser of science. In this book she has undertaken an extremely ambitious task, since laying the groundwork for braneworld models requires recapitulating most of twentieth century physics, including special and general relativity, quantum mechanics, particle physics and the standard model, and the rudiments of string theory. All of this results in a 500 page volume where we don't really get to the new stuff until about page 300. Now, this problem is generic to physics popularisations, but many others have handled it much better; Randall seems compelled to invent an off-the-wall analogy for every single technical item she describes, even when the description itself would be crystal clear to a reader encountering the material for the first time. You almost start to cringe—after every paragraph or two about actual physics, you know there's one coming about water sprinklers, ducks on a pond, bureaucrats shuffling paper, artists mixing paint, drivers and speed traps, and a host of others. There are also far too few illustrations in the chapters describing relativity and quantum mechanics; Isaac Asimov used to consider it a matter of pride to explain things in words rather than using a diagram, but Randall is (as yet) neither the wordsmith nor the explainer that Asimov was, but then who is?

There is a lot to like here, and I know of no other popular source which so clearly explains what may be discovered when the LHC fires up next year. Readers familiar with modern physics might check this book out of the library or borrow a copy from a friend and start reading at chapter 15, or maybe chapter 12 if you aren't up on the hierarchy problem in the standard model. This is a book which could have greatly benefited from a co-author with experience in science popularisation: Randall's technical writing (for example, her chapter in the Wheeler 90th birthday festschrift) is a model of clarity and concision; perhaps with more experience she'll get a better handle on communicating to a general audience.

February 2006 

Rees, Martin. Just Six Numbers: The Deep Forces That Shape the Universe. New York: Basic Books, 2000. ISBN 0-465-03672-4.

January 2001 

Rees, Martin. Our Final Hour. New York: Basic Books, 2003. ISBN 0-465-06862-6.

Rees, the English Astronomer Royal, writes with a literary tic one has become accustomed to in ideologically biased news reporting. Almost every person he names is labeled to indicate Rees' approbation or disdain for that individual's viewpoint. Freeman Dyson—Freeman Dyson!—is dismissed as a “futurist”, Ray Kurzweil and Esther Dyson as “gurus”, and Bjørn Lomborg as an “anti-gloom environmental propagandist”, while those he approves of such as Kurt Gödel (“great logician”), Arnold Schwarzenegger (“greatest Austrian-American body”), Luis Alvarez (“Nobel physicist”), and Bill Joy (“co-founder of Sun Microsystems, and the inventor of the Java computer language”) get off easier. (“Inventor of Java” is perhaps a tad overstated: while Joy certainly played a key rôle in the development of Java, the programming language was principally designed by James Gosling. But that's nothing compared to note 152 on page 204, where the value given for the approximate number of nucleons in the human body is understated by fifty-six orders of magnitude.) The U.K. edition bears the marginally more optimistic title, Our Final Century. but then everything takes longer in Britain.

July 2003 

Reeves, Richard. A Force of Nature. New York: W. W. Norton, 2008. ISBN 978-0-393-33369-5.

In 1851, the Crystal Palace Exhibition opened in London. It was a showcase of the wonders of industry and culture of the greatest empire the world had ever seen and attracted a multitude of visitors. Unlike present-day “World's Fair” boondoggles, it made money, and the profits were used to fund good works, including endowing scholarships for talented students from the far reaches of the Empire to study in Britain. In 1895, Ernest Rutherford, hailing from a remote area in New Zealand and recent graduate of Canterbury College in Christchurch, won a scholarship to study at Cambridge. Upon learning of the award in a field of his family's farm, he threw his shovel in the air and exclaimed, “That's the last potato I'll ever dig.” It was.

When he arrived at Cambridge, he could hardly have been more out of place. He and another scholarship winner were the first and only graduate students admitted who were not Cambridge graduates. Cambridge, at the end of the Victorian era, was a clubby, upper-class place, where even those pursuing mathematics were steeped in the classics, hailed from tony public schools, and spoke with refined accents. Rutherford, by contrast, was a rough-edged colonial, bursting with energy and ambition. He spoke with a bizarre accent (which he retained all his life) which blended the Scottish brogue of his ancestors with the curious intonations of the antipodes. He was anything but the ascetic intellectual so common at Cambridge—he had been a fierce competitor at rugby, spoke about three times as loud as was necessary (many years later, when the eminent Rutherford was tapped to make a radio broadcast from Cambridge, England to Cambridge, Massachusetts, one of his associates asked, “Why use radio?”), and spoke vehemently on any and all topics (again, long afterward, when a ceremonial portrait was unveiled, his wife said she was surprised the artist had caught him with his mouth shut).

But it quickly became apparent that this burly, loud, New Zealander was extraordinarily talented, and under the leadership of J.J. Thomson, he began original research in radio, but soon abandoned the field to pursue atomic research, which Thomson had pioneered with his discovery of the electron. In 1898, with Thomson's recommendation, Rutherford accepted a professorship at McGill University in Montreal. While North America was considered a scientific backwater in the era, the generous salary would allow him to marry his fiancée, who he had left behind in New Zealand until he could find a position which would support them.

At McGill, he and his collaborator Frederick Soddy, studying the radioactive decay of thorium, discovered that radioactive decay was characterised by a unique half-life, and was composed of two distinct components which he named alpha and beta radiation. He later named the most penetrating product of nuclear reactions gamma rays. Rutherford was the first to suggest, in 1902, that radioactivity resulted from the transformation of one chemical element into another—something previously thought impossible.

In 1907, Rutherford was offered, and accepted a chair of physics at the University of Manchester, where, with greater laboratory resources than he had had in Canada, pursued the nature of the products of radioactive decay. By 1907, by a clever experiment, he had identified alpha radiation (or particles, as we now call them) with the nuclei of helium atoms—nuclear decay was heavy atoms being spontaneously transformed into a lighter element and a helium nucleus.

Based upon this work, Rutherford won the Nobel Prize in Chemistry in 1908. As a person who considered himself first and foremost an experimental physicist and who was famous for remarking, “All science is either physics or stamp collecting”, winning the Chemistry Nobel had to feel rather odd. He quipped that while he had observed the transmutation of elements in his laboratory, no transmutation was as startling as discovering he had become a chemist. Still, physicist or chemist, his greatest work was yet to come.

In 1909, along with Hans Geiger (later to invent the Geiger counter) and Ernest Marsden, he conducted an experiment where high-energy alpha particles were directed against a very thin sheet of gold foil. The expectation was that few would be deflected and those only slightly. To the astonishment of the experimenters, some alpha particles were found to be deflected through large angles, some bouncing directly back toward the source. Geiger exclaimed, “It was almost as incredible as if you fired a 15-inch [battleship] shell at a piece of tissue paper and it came back and hit you.” It took two years before Rutherford fully understood and published what was going on, and it forever changed the concept of the atom. The only way to explain the scattering results was to replace the early model of the atom with one in which a diffuse cloud of negatively charged electrons surrounded a tiny, extraordinarily dense, positively charged nucleus (that word was not used until 1913). This experimental result fed directly into the development of quantum theory and the elucidation of the force which bound the particles in the nucleus together, which was not fully understood until more than six decades later.

In 1919 Rutherford returned to Cambridge to become the head of the Cavendish Laboratory, the most prestigious position in experimental physics in the world. Continuing his research with alpha emitters, he discovered that bombarding nitrogen gas with alpha particles would transmute nitrogen into oxygen, liberating a proton (the nucleus of hydrogen). Rutherford simultaneously was the first to deliberately transmute one element into another, and also to discover the proton. In 1921, he predicted the existence of the neutron, completing the composition of the nucleus. The neutron was eventually discovered by his associate, James Chadwick, in 1932.

Rutherford's discoveries, all made with benchtop apparatus and a small group of researchers, were the foundation of nuclear physics. He not only discovered the nucleus, he also found or predicted its constituents. He was the first to identify natural nuclear transmutation and the first to produce it on demand in the laboratory. As a teacher and laboratory director his legacy was enormous: eleven of his students and research associates went on to win Nobel prizes. His students John Cockcroft and Ernest Walton built the first particle accelerator and ushered in the era of “big science”. Rutherford not only created the science of nuclear physics, he was the last person to make major discoveries in the field by himself, alone or with a few collaborators, and with simple apparatus made in his own laboratory.

In the heady years between the wars, there were, in the public mind, two great men of physics: Einstein the theoretician and Rutherford the experimenter. (This perception may have understated the contributions of the creators of quantum mechanics, but they were many and less known.) Today, we still revere Einstein, but Rutherford is less remembered (except in New Zealand, where everybody knows his name and achievements). And yet there are few experimentalists who have discovered so much in their lifetimes, with so little funding and the simplest apparatus. Rutherford, that boisterous, loud, and restless colonial, figured out much of what we now know about the atom, largely by himself, through a multitude of tedious experiments which often failed, and he should rightly be regarded as a pillar of 20th century physics.

This is the thousandth book to appear since I began to keep the reading list in January 2001.

February 2015 

Reich, Eugenie Samuel. Plastic Fantastic. New York: St. Martin's Press, 2009. ISBN 978-0-230-62384-2.

Boosters of Big Science, and the politicians who rely upon its pronouncements to justify their policy prescriptions often cite the self-correcting nature of the scientific process: peer review subjects the work of researchers to independent and dispassionate scrutiny before results are published, and should an incorrect result make it into print, the failure of independent researchers to replicate it will inevitably call it into question and eventually cause it to be refuted.

Well, that's how it works in theory. Theory is very big in contemporary Big Science. This book is about how things work in fact, in the real world, and it's quite a bit different. At the turn of the century, there was no hotter property in condensed matter physics than Hendrik Schön, a junior researcher at Bell Labs who, in rapid succession reported breakthroughs in electronic devices fabricated from organic molecules including:

• Organic field effect transistors
• Field-induced superconductivity in organic crystals
• Fractional quantum Hall effect in organic materials
• Organic crystal laser
• Light emitting organic transistor
• Organic Josephson junction
• High temperature superconductivity in C₆₀
• Single electron organic transistors

In the year 2001, Schön published a paper in a peer reviewed journal at a rate of one every eight days, with many reaching the empyrean heights of Nature, Science, and Physical Review. Other labs were in awe of his results, and puzzled because every attempt they made to replicate his experiments failed, often in ways which seemed to indicate the descriptions of experiments he published were insufficient for others to replicate them. Theorists also raised their eyebrows at Schön's results, because he claimed breakdown properties of sputtered aluminium oxide insulating layers far beyond measured experimental results, and behaviour of charge transport in his organic substrates which didn't make any sense according to the known properties of such materials.

The experimenters were in a tizzy, trying to figure out why they couldn't replicate Schön's results, while the theorists were filling blackboards trying to understand how his incongruous results could possibly make sense. His superiors were basking in the reflected glory of his ascendence into the élite of experimental physicists and the reflection of his glory upon their laboratory.

In April 2002, while waiting in the patent attorney's office at Bell Labs, researchers Julia Hsu and Lynn Loo were thumbing through copies of Schön's papers they'd printed out as background documentation for the patent application they were preparing, when Loo noticed that two graphs of inverter outputs, one in a Nature paper describing a device made of a layer of thousands of organic molecules, and another in a Science paper describing an inverter made of just one or two active molecules were identical, right down to the instrumental noise. When this was brought to the attention of Schön's manager and word of possible irregularities in Schön's publications began to make its way through the condensed matter physics grapevine, his work was subjected to intense scrutiny both within Bell Labs and by outside researchers, and additional instances of identical graphs re-labelled for entirely different experiments came to hand. Bell Labs launched a formal investigation in May 2002, which concluded, in a report issued the following September, that Schön had committed at least 16 instances of scientific misconduct, fabricating the experimental data he reported from mathematical functions, with no evidence whatsoever that he had ever built the devices he claimed to have, or performed the experiments described in his papers. A total of twenty-one papers authored by Schön in Science, Nature, and Physical Review were withdrawn, as well as a number in less prestigious venues.

What is fascinating in this saga of flat-out fraud and ultimate exposure and disgrace is how completely the much-vaunted system of checks and balances of industrial scale Big Science and peer review in the most prestigious journals completely fell on its face at the hands of a fraudster in a junior position with little or no scientific track record who was willing to make up data to confirm the published expectations of the theorists, and figured out how to game the peer review system, using criticisms of his papers as a guide to make up additional data to satisfy the objections of the referees. As a former manager of a group of ambitious and rambunctious technologists, what strikes me is how utterly Schön's colleagues and managers at Bell Labs failed in overseeing his work and vetting his results. “Extraordinary claims require extraordinary evidence”, and Schön was making and publishing extraordinary claims at the rate of almost one a week in 2001, and yet not once did anybody at Bell Labs insist on observing him perform one of the experiments he claimed to be performing, even after other meticulous experimenters in laboratories around the world reported that they were unable to replicate his results. Think about it—if a junior software developer in your company claimed to have developed a miraculous application, wouldn't you want to see a demo before issuing a press release about it and filing a patent application? And yet nobody at Bell Labs thought to do so with Schön's work.

The lessons from this episode are profound, and I see little evidence that they have been internalised by the science establishment. A great deal of experimental science is now guided by the expectations of theorists; it is difficult to obtain funding for an experimental program which looks for effects not anticipated by theory. In such an environment, an unscrupulous scientist willing to make up data that conforms to the prejudices of the theorists may be able to publish in prestigious journals and be considered a rising star of science based on an entirely fraudulent corpus of work. Because scientists, especially in the Anglo-Saxon culture, are loath to make accusations of fraud (as the author notes, in the golden age of British science such an allegation might well result in a duel being fought), failure to replicate experimental results is often assumed to be a failure by the replicator to precisely reproduce the circumstances of the original investigator, not to call into question the veracity of the reported work. Schön's work consisted of desktop experiments involving straightforward measurements of electrical properties of materials, which were about as simple as anything in contemporary science to evaluate and independently replicate. Now think of how vulnerable research on far less clear cut topics such as global climate, effects of diet on public health, and other topics would be to fraudulent, agenda-driven “research”. Also, Schön got caught only because he became sloppy in his frenzy of publication, duplicating graphs and data sets from one paper to another. How long could a more careful charlatan get away with it?

Quite aside from the fascinating story and its implications for the integrity of the contemporary scientific enterprise, this is a superbly written narrative which reads more like a thriller than an account of a regrettable episode in science. But it is entirely factual, and documented with extensive end notes citing original sources.

August 2010 

Robinson, Andrew. The Last Man Who Knew Everything. New York: Pi Press, 2006. ISBN 0-13-134304-1.

The seemingly inexorable process of specialisation in the sciences and other intellectual endeavours—the breaking down of knowledge into categories so narrow and yet so deep that their mastery at the professional level seems to demand forsaking anything beyond a layman's competence in other, even related fields, is discouraging to those who believe that some of the greatest insights come from the cross-pollination of concepts from subjects previously considered unrelated. The twentieth century was inhospitable to polymaths—even within a single field such as physics, ever narrower specialities proliferated, with researchers interacting little with those working in other areas. The divide between theorists and experimentalists has become almost impassable; it is difficult to think of a single individual who achieved greatness in both since Fermi, and he was born in 1901.

As more and more becomes known, it is inevitable that it is increasingly difficult to cram it all into one human skull, and the investment in time to master a variety of topics becomes disproportionate to the length of a human life, especially since breakthrough science is generally the province of the young. And yet, one wonders whether the conventional wisdom that hyper-specialisation is the only way to go and that anybody who aspires to broad and deep understanding of numerous subjects must necessarily be a dilettante worthy of dismissal, might underestimate the human potential and discourage those looking for insights available only by synthesising the knowledge of apparently unrelated disciplines. After all, mathematicians have repeatedly discovered deep connections between topics thought completely unrelated to one another; why shouldn't this be the case in the sciences, arts, and humanities as well?

The life of Thomas Young (1773–1829) is an inspiration to anybody who seeks to understand as much as possible about the world in which they live. The eldest of ten children of a middle class Quaker family in southwest England (his father was a cloth merchant and later a banker), from childhood he immersed himself in every book he could lay his hands upon, and in his seventeenth year alone, he read Newton's Principia and Opticks, Blackstone's Commentaries, Linnaeus, Euclid's Elements, Homer, Virgil, Sophocles, Cicero, Horace, and many other classics in the original Greek or Latin. At age 19 he presented a paper on the mechanism by which the human eye focuses on objects at different distances, and on its merit was elected a Fellow of the Royal Society a week after his 21st birthday.

Young decided upon a career in medicine and studied in Edinburgh, Göttingen, and Cambridge, continuing his voracious reading and wide-ranging experimentation in whatever caught his interest, then embarked upon a medical practice in London and the resort town of Worthing, while pursuing his scientific investigations and publications, and popularising science in public lectures at the newly founded Royal Institution.

The breadth of Young's interests and contributions have caused some biographers, both contemporary and especially more recent, to dismiss him as a dilettante and dabbler, but his achievements give lie to this. Had the Nobel Prize existed in his era, he would almost certainly have won two (Physics for the wave theory of light, explanation of the phenomena of diffraction and interference [including the double slit experiment], and birefringence and polarisation; plus Physiology or Medicine for the explanation of the focusing of the eye [based, in part, upon some cringe-inducing experiments he performed upon himself], the trireceptor theory of colour vision, and the discovery of astigmatism), and possibly three (Physics again, for the theory of elasticity of materials: “Young's modulus” is a standard part of the engineering curriculum to this day).

But he didn't leave it at that. He was fascinated by languages since childhood, and in addition to the customary Latin and Greek, by age thirteen had taught himself Hebrew and read thirty chapters of the Hebrew Bible all by himself. In adulthood he undertook an analysis of four hundred different languages (pp. 184–186) ranging from Chinese to Cherokee, with the goal of classifying them into distinct families. He coined the name “Indo-European” for the group to which most Western languages belong. He became fascinated with the enigma of Egyptian hieroglyphics, and his work on the Rosetta Stone provided the first breakthrough and the crucial insight that hieroglyphic writing was a phonetic alphabet, not a pictographic language like Chinese. Champollion built upon Young's work in his eventual deciphering of hieroglyphics. Young continued to work on the fiendishly difficult demotic script, and was the first person since the fall of the Roman Empire to be able to read some texts written in it.

He was appointed secretary of the Board of Longitude and superintendent of the Nautical Almanac, and was instrumental in the establishment of a Southern Hemisphere observatory at the Cape of Good Hope. He consulted with the admiralty on naval architecture, with the House of Commons on the design for a replacement to the original London Bridge, and served as chief actuary for a London life insurance company and did original research on mortality in different parts of Britain.

Stereotypical characters from fiction might cause you to expect that such an intellect might be a recluse, misanthrope, obsessive, or seeker of self-aggrandisement. But no…, “He was a lively, occasionally caustic letter writer, a fair conversationalist, a knowledgeable musician, a respectable dancer, a tolerable versifier, an accomplished horseman and gymnast, and throughout his life, a participant in the leading society of London and, later, Paris, the intellectual capitals of his day” (p. 12). Most of the numerous authoritative articles he contributed to the Encyclopedia Britannica, including “Bridge”, “Carpentry”, “Egypt”, “Languages”, “Tides”, and “Weights and measures”, as well as 23 biographies, were published anonymously. And he was happily married from age 31 until the end of his life.

Young was an extraordinary person, but he never seems to have thought of himself as exceptional in any way other than his desire to understand how things worked and his willingness to invest as much time and effort as it took at arrive at the goals he set for himself. Reading this book reminded me of a remark by Admiral Hyman G. Rickover, “The only way to make a difference in the world is to put ten times as much effort into everything as anyone else thinks is reasonable. It doesn't leave any time for golf or cocktails, but it gets things done.” Young's life is a testament to just how many things one person can get done in a lifetime, enjoying every minute of it and never losing balance, by judicious application of this principle.

March 2007 

Ryan, Craig. Sonic Wind. New York: Livewright Publishing, 2018. ISBN 978-0-631-49191-0.

Prior to the 1920s, most aircraft pilots had no means of escape in case of mechanical failure or accident. During World War I, one out of every eight combat pilots was shot down or killed in a crash. Germany experimented with cumbersome parachutes stored in bags in a compartment behind the pilot, but these often failed to deploy properly if the plane was in a spin or became tangled in the aircraft structure after deployment. Still, they did save the lives of a number of German pilots. (On the other hand, one of them was Hermann Göring.) Allied pilots were not issued parachutes because their commanders feared the loss of planes more than pilots, and worried pilots would jump rather than try to save a damaged plane.

From the start of World War II, military aircrews were routinely issued parachutes, and backpack or seat pack parachutes with ripcord deployment had become highly reliable. As the war progressed and aircraft performance rapidly increased, it became clear that although parachutes could save air crew, physically escaping from a damaged plane at high velocities and altitudes was a formidable problem. The U.S. P-51 Mustang, of which more than 15,000 were built, cruised at 580 km/hour and had a maximum speed of 700 km/hour. It was physically impossible for a pilot to escape from the cockpit into such a wind blast, and even if they managed to do so, they would likely be torn apart by collision with the fuselage or tail an instant later. A pilot's only hope was that the plane would slow to a speed at which escape was possible before crashing into the ground, bursting into flames, or disintegrating.

In 1944, when the Nazi Luftwaffe introduced the first operational jet fighter, the Messerschmitt Me 262, capable of 900 km/hour flight, they experimented with explosive-powered ejection seats, but never installed them in this front-line fighter. After the war, with each generation of jet fighters flying faster and higher than the previous, and supersonic performance becoming routine, ejection seats became standard equipment in fighter and high performance bomber aircraft, and saved many lives. Still, by the mid-1950s, one in four pilots who tried to eject was killed in the attempt. It was widely believed that the forces of blasting a pilot out of the cockpit, rapid deceleration by atmospheric friction, and wind blast at transonic and supersonic speeds were simply too much for the human body to endure. Some aircraft designers envisioned “escape capsules” in which the entire crew cabin would be ejected and recovered, but these systems were seen to be (and proved when tried) heavy and potentially unreliable.

John Paul Stapp's family came from the Hill Country of south central Texas, but he was born in Brazil in 1910 while his parents were Baptist missionaries there. After high school in Texas, he enrolled in Baylor University in Waco, initially studying music but then switching his major to pre-med. Upon graduation in 1931 with a major in zoology and minor in chemistry, he found that in the depths of the Depression there was no hope of affording medical school, so he enrolled in an M.A. program in biophysics, occasionally dining on pigeons he trapped on the roof of the biology building and grilled over Bunsen burners in the laboratory. He then entered a Ph.D. program in biophysics at the University of Texas, Austin, receiving his doctorate in 1940. Before leaving Austin, he was accepted by the medical school at the University of Minnesota, which promised him employment as a research assistant and instructor to fund his tuition.

In October 1940, with the possibility that war in Europe and the Pacific might entangle the country, the U.S. began military conscription. When the numbers were drawn from the fishbowl, Stapp's was 15th from the top. As a medical student, he received an initial deferment, but when it expired he joined the regular Army under a special program for medical students. While completing medical school, he would receive private's pay of US$ 32 a month (around US$7000 a year in today's money), which would help enormously with tuition and expenses. In December 1943 Stapp received his M.D. degree and passed the Minnesota medical board examination. He was commissioned as a second lieutenant in the Army Medical Corps and placed on suspended active duty for his internship in a hospital in Duluth, Minnesota, where he delivered 200 babies and assisted in 225 surgeries. He found he delighted in emergency and hands-on medicine. In the fall of 1944 he went on full active duty and began training in field medicine. After training, he was assigned as a medical officer at Lincoln Army Air Field in Nebraska, where he would combine graduate training with hospital work.

Stapp had been fascinated by aviation and the exploits of pioneers such as Charles Lindbergh and the stratospheric balloon explorers of the 1930s, and found working at an air base fascinating, sometimes arranging to ride along in training missions with crews he'd treated in the hospital. In April 1945 he was accepted by the Army School of Aviation Medicine in San Antonio, where he and his class of 150 received intense instruction in all aspects of human physiology relating to flight. After graduation and a variety of assignments as a medical officer, he was promoted to captain and invited to apply to the Aero Medical Laboratory at Wright Field in Dayton, Ohio for a research position in the Biophysics Branch. On the one hand, this was an ideal position for the intellectually curious Stapp, as it would combine his Ph.D. work and M.D. career. On the other, he had only eight months remaining in his service commitment, and he had long planned to leave the Army to pursue a career as a private physician. Stapp opted for the challenge and took the post at Wright.

Starting work, he was assigned to the pilot escape technology program as a “project engineer”. He protested, “I'm a doctor, not an engineer!”, but settled into the work and, being fluent in German, was assigned to review 1200 pages of captured German documents relating to crew ejection systems and their effects upon human subjects. Stapp was appalled by the Nazis' callous human experimentation, but, when informed that the Army intended to destroy the documents after his study was complete, took the initiative to preserve them, both for their scientific content and as evidence of the crimes of those whose research produced it.

The German research and the work of the branch in which Stapp worked had begun to persuade him that the human body was far more robust than had been assumed by aircraft designers and those exploring escape systems. It was well established by experiments in centrifuges at Wright and other laboratories that the maximum long-term human tolerance for acceleration (g-force) without special equipment or training was around six times that of Earth's gravity, or 6 g. Beyond that, subjects would lose consciousness, experience tissue damage due to lack of blood flow, or structural damage to the skeleton and/or internal organs. However, a pilot ejecting from a high performance aircraft experienced something entirely different from a subject riding in a centrifuge. Instead of a steady crush by, say, 6 g, the pilot would be subjected to much higher accelerations, perhaps on the order of 20—40 g, with an onset of acceleration (“jerk”) of 500 g per second. The initial blast of the mortar or rockets firing the seat out of the cockpit would be followed by a sharp pulse of deceleration as the pilot was braked from flight speed by air friction, during which he would be subjected to wind blast potentially ten times as strong as any hurricane. Was this survivable at all, and if so, what techniques and protective equipment might increase a pilot's chances of enduring the ordeal?

While pondering these problems and thinking about ways to research possible solutions under controlled conditions, Stapp undertook another challenge: providing supplemental oxygen to crews at very high altitudes. Stapp volunteered as a test subject as well as medical supervisor and began flight tests with a liquid oxygen breathing system on high altitude B-17 flights. Crews flying at these altitudes in unpressurised aircraft during World War II and afterward had frequently experienced symptoms similar to “the bends” (decompression sickness) which struck divers who ascended too quickly from deep waters. Stapp diagnosed the cause as identical: nitrogen dissolved in the blood coming out of solution as bubbles and pooling in joints and other bodily tissues. He devised a procedure of oxygen pre-breathing, where crews would breathe pure oxygen for half an hour before taking off on a high altitude mission, which completely eliminated the decompression symptoms. The identical procedure is used today by astronauts before they begin extravehicular activities in space suits using pure oxygen at low pressure.

From the German documents he studied, Stapp had become convinced that the tool he needed to study crew escape was a rocket propelled sled, running on rails, with a brake mechanism that could be adjusted to provide a precisely calibrated deceleration profile. When he learned that the Army was planning to build such a device at Muroc Army Air Base in California, he arranged to be put in charge of Project MX-981 with a charter to study the “effects of deceleration forces of high magnitude on man”. He arrived at Muroc in March 1947, along with eight crash test dummies to be used in the experiments. If Muroc (now Edwards Air Force Base) of the era was legendary for its Wild West accommodations (Chuck Yeager would not make his first supersonic flight there until October of that year), the North Base, where Stapp's project was located, was something out of Death Valley Days. When Stapp arrived to meet his team of contractors from Northrop Corporation they struck the always buttoned-down Stapp like a “band of pirates”. He also discovered the site had no electricity, no running water, no telephone, and no usable buildings. The Army, preoccupied with its glamourous high speed aviation projects, had neither interest in what amounted to a rocket powered train with a very short track, nor much inclination to provide it the necessary resources. Stapp commenced what he came to call the Battle of Muroc, mastering the ancient military art of scrounging and exchanging favours to get the material he needed and the work done.

As he settled in at Muroc and became acquainted with his fellow denizens of the desert, he was appalled to learn that the Army provided medical care only for active duty personnel, and that civilian contractors and families of servicemen, even the exalted test pilots, had to drive 45 miles to the nearest clinic. He began to provide informal medical care to all comers, often making house calls in the evening hours on his wheezing scooter, in return for home cooked dinners. This built up a network of people who owed him favours, which he was ready to call in when he needed something. He called this the “Curbstone Clinic”, and would continue the practice throughout his career. After some shaky starts and spectacular failures due to unreliable surplus JATO rockets, the equipment was ready to begin experiments with crash test dummies.

Stapp had always intended that the tests with dummies would be simply a qualification phase for later tests with human and animal subjects, and he would ask no volunteer to do something he wouldn't try himself. Starting in December, 1947, Stapp personally made increasingly ambitious runs on the sled, starting at “only” 10 g deceleration and building to 35 g with an onset jerk of 1000 g/second. The runs left him dizzy and aching, but very much alive and quick to recover. Although far from approximating the conditions of ejection from a supersonic fighter, he had already demonstrated that the Air Force's requirements for cockpit seats and crew restraints, often designed around a 6 g maximum shock, were inadequate and deadly. Stapp was about to start making waves, and some of the push-back would be daunting. He was ordered to cease all human experimentation for at least three months.

Many Air Force officers (for the Air Force had been founded in September 1947 and taken charge of the base) would have saluted and returned to testing with instrumented dummies. Stapp, instead, figured out how to obtain thirty adult chimpanzees, along with the facilities needed to house and feed them, and resumed his testing, with anæsthetised animals, up to the limits of survival. Stapp was, and remained throughout his career, a strong advocate for the value of animal experimentation. It was a grim business, but at the time Muroc was frequently losing test pilots at the rate of one a week, and Stapp believed that many of these fatalities were unnecessary and could be avoided with proper escape and survival equipment, which could only be qualified through animal and cautious human experimentation.

By September 1949, approval to resume human testing was given, and Stapp prepared for new, more ambitious runs, with the subject facing forward on the sled instead of backward as before, which would more accurately simulate the forces in an ejection or crash and expose him directly to air blast. He rapidly ramped up the runs, reaching 32 g without permanent injury. To avoid alarm on the part of his superiors in Dayton, a “slight error” was introduced in the reports he sent: all g loads from the runs were accidentally divided by two.

Meanwhile, Stapp was ramping up his lobbying for safer seats in Air Force transport planes, arguing that the existing 6 g forward facing seats and belts were next to useless in many survivable crashes. Finally, with the support of twenty Air Force generals, in 1950 the Air Force adopted a new rear-facing standard seat and belt rated for 16 g which weighed only two pounds more than those it replaced. The 16 g requirement (although not the rearward-facing orientation, which proved unacceptable to paying customers) remains the standard for airliner seats today, seven decades later.

In June, 1951, Stapp made his final run on the MX-981 sled at what was now Edwards Air Force Base, decelerating from 180 miles per hour (290 km/h) to zero in 31 feet (9.45 metres), at 45.4 g, a force comparable to many aircraft and automobile accidents. The limits of the 2000 foot track (and the human body) had been reached. But Stapp was not done: the frontier of higher speeds remained. Shortly thereafter, he was promoted to lieutenant colonel and given command of what was called the Special Projects Section of the Biophysics Branch of the Aero Medical Laboratory. He was reassigned to Holloman Air Force Base in New Mexico, where the Air Force was expanding its existing 3500 foot rocket sled track to 15,000 feet (4.6 km), allowing testing at supersonic speeds. (The Holloman High Speed Test Track remains in service today, having been extended in a series of upgrades over the years to a total of 50,917 feet (15.5 km) and a maximum speed of Mach 8.6, or 2.9 km/sec [6453 miles per hour].)

Northrop was also contractor for the Holloman sled, and devised a water brake system which would be more reliable and permit any desired deceleration profile to be configured for a test. An upgraded instrumentation system would record photographic and acceleration measurements with much better precision than anything at Edwards. The new sled was believed to be easily capable of supersonic speeds and was named Sonic Wind. By March 1954, the preliminary testing was complete and Stapp boarded the sled. He experienced a 12 g acceleration to the peak speed of 421 miles per hour, then 22 g deceleration to a full stop, all in less than eight seconds. He walked away, albeit a little wobbly. He had easily broken the previous land speed record of 402 miles per hour and become “the fastest man on Earth.” But he was not done.

On December 10th, 1954, Stapp rode Sonic Wind, powered by nine solid rocket motors. Five seconds later, he was travelling at 639 miles per hour, faster than the .45 ACP round fired by the M1911A1 service pistol he was issued as an officer, around Mach 0.85 at the elevation of Holloman. The water brakes brought him to a stop in 1.37 seconds, a deceleration of 46.2 g. He survived, walked away (albeit just few steps to the ambulance), and although suffering from vision problems for some time afterward, experienced no lasting consequences. It was estimated that the forces he survived were equivalent to those from ejecting at an altitude of 36,000 feet from an airplane travelling at 1800 miles per hour (Mach 2.7). As this was faster than any plane the Air Force had in service or on the drawing board, he proved that, given a suitable ejection seat, restraints, and survival equipment, pilots could escape and survive even under these extreme circumstances. The Big Run, as it came to be called, would be Stapp's last ride on a rocket sled and the last human experiment on the Holloman track. He had achieved the goal he set for himself in 1947: to demonstrate that crew survival in high performance aircraft accidents was a matter of creative and careful engineering, not the limits of the human body. The manned land speed record set on the Big Run would stand until October 1983, when Richard Noble's jet powered Thrust2 car set a new record of 650.88 miles per hour in the Nevada desert. Stapp remarked at the time that Noble had gone faster but had not, however, stopped from that speed in less than a second and a half.

From the early days of Stapp's work on human tolerance to deceleration, he was acutely aware that the forces experienced by air crew in crashes were essentially identical to those in automobile accidents. As a physician interested in public health issues, he had noted that the Air Force was losing more personnel killed in car crashes than in airplane accidents. When the Military Air Transport Service (MATS) adopted his recommendation and installed 16 g aft-facing seats in its planes, deaths and injuries from crashes had fallen by two-thirds. By the mid 1950s, the U.S. was suffering around 35,000 fatalities per year in automobile accidents—comparable to a medium-sized war—year in and year out, yet next to nothing had been done to make automobiles crash resistant and protect their occupants in case of an accident. Even the simplest precaution of providing lap belts, standard in aviation for decades, had not been taken; seats were prone to come loose and fly forward even in mild impacts; steering columns and dashboards seemed almost designed to impale drivers and passengers; and “safety” glass often shredded the flesh of those projected through it in a collision.

In 1954, Stapp turned some of his celebrity as the fastest man on Earth toward the issue of automobile safety and organised, in conjunction with the Society of Automotive Engineers (SAE), the first Automobile Crash Research Field Demonstration and Conference, which was attended by representatives of all of the major auto manufacturers, medical professional societies, and public health researchers. Stapp and the SAE insisted that the press be excluded: he wanted engineers from the automakers free to speak without fear their candid statements about the safety of their employers' products would be reported sensationally. Stapp conducted a demonstration in which a car was towed into a fixed barrier at 40 miles an hour with two dummies wearing restraints and two others just sitting in the seats. The belted dummies would have walked away, while the others flew into the barrier and would have almost certainly been killed. It was at this conference that many of the attendees first heard the term “second collision”. In car crashes, it was often not the crash of the car into another car or a barrier that killed the occupants: it was their colliding with dangerous items within the vehicle after flying loose following the initial impact.

Despite keeping the conference out of the press, word of Stapp's vocal advocacy of automobile safety quickly reached the auto manufacturers, who were concerned both about the marketing impact of the public becoming aware not only of the high level of deaths on the highways but also the inherent (and unnecessary) danger of their products to those who bought them, and also the bottom-line impact of potential government-imposed safety mandates. Auto state congressmen got the message, and the Air Force heard it from them: the Air Force threatened to zero out aeromedical research funding unless car crash testing was terminated. It was.

Still, the conferences continued (they would eventually be renamed “Stapp Car Crash Conferences”), and Stapp became a regular witness before congressional committees investigating automobile safety. Testifying about whether it was appropriate for Air Force funds to be used in studying car crashes, in 1957 he said, “I have done autopsies on aircrew members who died in airplane crashes. I have also performed autopsies on aircrew members who died in car crashes. The only conclusion I could come to is that they were just as dead after a car crash as they were after an airplane crash.” He went on to note that simply mandating seatbelts in Air Force ground vehicles would save around 125 lives a year, and if they were installed and used by the occupants of all cars in the U.S., around 20,000 lives—more than half the death toll—could be saved. When he appeared before congress, he bore not only the credentials of a medical doctor, Ph.D. in biophysics, Air Force colonel, but the man who had survived more violent decelerations equivalent to a car crash than any other human.

It was not until the 1960s that a series of mandates were adopted in the U.S. which required seat belts, first in the front seat and eventually for all passengers. Testifying in 1963 at a hearing to establish a National Accident Prevention Center, Stapp noted that the Air Force, which had already adopted and required the use of seat belts, had reduced fatalities in ground vehicle accidents by 50% with savings estimated at US$ 12 million per year. In September 1966, President Lyndon Johnson signed two bills, the National Traffic and Motor Vehicle Safety Act and the Highway Safety Act, creating federal agencies to research vehicle safety and mandate standards. Standing behind the president was Colonel John Paul Stapp: the long battle was, if not won, at least joined.

Stapp had hoped for a final promotion to flag rank before retirement, but concluded he had stepped on too many toes and ignored too many Pentagon directives during his career to ever wear that star. In 1967, he was loaned by the Air Force to the National Highway Traffic Safety Administration to continue his auto safety research. He retired from the Air Force in 1970 with the rank of full colonel and in 1973 left what he had come to call the “District of Corruption” to return to New Mexico. He continued to attend and participate in the Stapp Car Crash Conferences, his last being the Forty-Third in 1999. He died at his home in Alamogordo, New Mexico in November that year at the age of 89.

In his later years, John Paul Stapp referred to the survivors of car crashes who would have died without the equipment designed and eventually mandated because of his research as “the ghosts that never happened”. In 1947, when Stapp began his research on deceleration and crash survival, motor vehicle deaths in the U.S. were 8.41 per 100 million vehicle miles travelled (VMT). When he retired from the Air Force in 1970, after adoption of the first round of seat belt and auto design standards, they had fallen to 4.74 (which covers the entire fleet, many of which were made before the adoption of the new standards). At the time of his death in 1999, fatalities per 100 million VMT were 1.55, an improvement in safety of more than a factor of five. Now, Stapp was not solely responsible for this, but it was his putting his own life on the line which showed that crashes many considered “unsurvivable” were nothing of the sort with proper engineering and knowledge of human physiology. There are thousands of aircrew and tens or hundreds of thousands of “ghosts that never happened” who owe their lives to John Paul Stapp. Maybe you know one; maybe you are one. It's worth a moment remembering and giving thanks to the largely forgotten man who saved them.

February 2020 

Scheider, Walter. A Serious But Not Ponderous Book About Nuclear Energy. Ann Arbor MI: Cavendish Press, 2001. ISBN 0-9676944-2-6.

May 2001 

Segrè, Gino and Bettina Hoerlin. The Pope of Physics. New York: Henry Holt, 2016. ISBN 978-1-62779-005-5.

By the start of the 20th century, the field of physics had bifurcated into theoretical and experimental specialties. While theorists and experimenters were acquainted with the same fundamentals and collaborated, with theorists suggesting phenomena to be explored in experiments and experimenters providing hard data upon which theorists could build their models, rarely did one individual do breakthrough work in both theory and experiment. One outstanding exception was Enrico Fermi, whose numerous achievements seemed to jump effortlessly between theory and experiment.

Fermi was born in 1901 to a middle class family in Rome, the youngest of three children born in consecutive years. As was common at the time, Enrico and his brother Giulio were sent to be wet-nursed and raised by a farm family outside Rome and only returned to live with their parents when two and a half years old. His father was a division head in the state railway and his mother taught elementary school. Neither parent had attended university, but hoped all of their children would have the opportunity. All were enrolled in schools which concentrated on the traditional curriculum of Latin, Greek, and literature in those languages and Italian. Fermi was attracted to mathematics and science, but little instruction was available to him in those fields.

At age thirteen, the young Fermi made the acquaintance of Adolfo Amidei, an engineer who worked with his father. Amidei began to loan the lad mathematics and science books, which Fermi devoured—often working out solutions to problems which Amidei was unable to solve. Within a year, studying entirely on his own, he had mastered geometry and calculus. In 1915, Fermi bought a used book, Elementorum Physicæ Mathematica, at a flea market in Rome. Published in 1830 and written entirely in Latin, it was a 900 page compendium covering mathematical physics of that era. By that time, he was completely fluent in the language and the mathematics used in the abundant equations, and worked his way through the entire text. As the authors note, “Not only was Fermi the only twentieth-century physics genius to be entirely self-taught, he surely must be the only one whose first acquaintance with the subject was through a book in Latin.”

At sixteen, Fermi skipped the final year of high school, concluding it had nothing more to teach him, and with Amidei's encouragement, sat for a competitive examination for a place at the elite Sculoa Normale Superiore, which provided a complete scholarship including room and board to the winners. He ranked first in all of the examinations and left home to study in Pisa. Despite his talent for and knowledge of mathematics, he chose physics as his major—he had always been fascinated by mechanisms and experiments, and looked forward to working with them in his career. Italy, at the time a leader in mathematics, was a backwater in physics. The university in Pisa had only one physics professor who, besides having already retired from research, had knowledge in the field not much greater than Fermi's own. Once again, this time within the walls of a university, Fermi would teach himself, taking advantage of the university's well-equipped library. He taught himself German and English in addition to Italian and French (in which he was already fluent) in order to read scientific publications. The library subscribed to the German journal Zeitschrift für Physik, one of the most prestigious sources for contemporary research, and Fermi was probably the only person to read it there. In 1922, after completing a thesis on X-rays and having already published three scientific papers, two on X-rays and one on general relativity (introducing what are now called Fermi coordinates, the first of many topics in physics which would bear his name), he received his doctorate in physics, magna cum laude. Just twenty-one, he had his academic credential, published work to his name, and the attention of prominent researchers aware of his talent. What he lacked was the prospect of a job in his chosen field.

Returning to Rome, Fermi came to the attention of Orso Mario Corbino, a physics professor and politician who had become a Senator of the Kingdom and appointed minister of public education. Corbino's ambition was to see Italy enter the top rank of physics research, and saw in Fermi the kind of talent needed to achieve this goal. He arranged a scholarship so Fermi could study physics in one the centres of research in northern Europe. Fermi chose Göttingen, Germany, a hotbed of work in the emerging field of quantum mechanics. Fermi was neither particularly happy nor notably productive during his eight months there, but was impressed with the German style of research and the intellectual ferment of the large community of German physicists. Henceforth, he published almost all of his research in either German or English, with a parallel paper submitted to an Italian journal. A second fellowship allowed him to spend 1924 in the Netherlands, working with Paul Ehrenfest's group at Leiden, deepening his knowledge of statistical and quantum mechanics.

Finally, upon returning to Italy, Corbino and his colleague Antonio Garbasso found Fermi a post as a lecturer in physics in Florence. The position paid poorly and had little prestige, but at least it was a step onto the academic ladder, and Fermi was happy to accept it. There, Fermi and his colleague Franco Rasetti did experimental work measuring the spectra of atoms under the influence of radio frequency fields. Their work was published in prestigious journals such as Nature and Zeitschrift für Physik.

In 1925, Fermi took up the problem of reconciling the field of statistical mechanics with the discovery by Wolfgang Pauli of the exclusion principle, a purely quantum mechanical phenomenon which restricts certain kinds of identical particles from occupying the same state at the same time. Fermi's paper, published in 1926, resolved the problem, creating what is now called Fermi-Dirac statistics (British physicist Paul Dirac independently discovered the phenomenon, but Fermi published first) for the particles now called fermions, which include all of the fundamental particles that make up matter. (Forces are carried by other particles called bosons, which go beyond the scope of this discussion.)

This paper immediately elevated the twenty-five year old Fermi to the top tier of theoretical physicists. It provided the foundation for understanding of the behaviour of electrons in solids, and thus the semiconductor technology upon which all our modern computing and communications equipment is based. Finally, Fermi won what he had aspired to: a physics professorship in Rome. In 1928, he married Laura Capon, whom he had first met in 1924. The daughter of an admiral in the World War I Italian navy, she was a member of one of the many secular and assimilated Jewish families in Rome. She was less than impressed on first encountering Fermi:

He shook hands and gave me a friendly grin. You could call it nothing but a grin, for his lips were exceedingly thin and fleshless, and among his upper teeth a baby tooth too lingered on, conspicuous in its incongruity. But his eyes were cheerful and amused.

Both Laura and Enrico shared the ability to see things precisely as they were, then see beyond that to what they could become.

In Rome, Fermi became head of the mathematical physics department at the Sapienza University of Rome, which his mentor, Corbino, saw as Italy's best hope to become a world leader in the field. He helped Fermi recruit promising physicists, all young and ambitious. They gave each other nicknames: ecclesiastical in nature, befitting their location in Rome. Fermi was dubbed Il Papa (The Pope), not only due to his leadership and seniority, but because he had already developed a reputation for infallibility: when he made a calculation or expressed his opinion on a technical topic, he was rarely if ever wrong. Meanwhile, Mussolini was increasing his grip on the country. In 1929, he announced the appointment of the first thirty members of the Royal Italian Academy, with Fermi among the laureates. In return for a lifetime stipend which would put an end to his financial worries, he would have to join the Fascist party. He joined. He did not take the Academy seriously and thought its comic opera uniforms absurd, but appreciated the money.

By the 1930s, one of the major mysteries in physics was beta decay. When a radioactive nucleus decayed, it could emit one or more kinds of radiation: alpha, beta, or gamma. Alpha particles had been identified as the nuclei of helium, beta particles as electrons, and gamma rays as photons: like light, but with a much shorter wavelength and correspondingly higher energy. When a given nucleus decayed by alpha or gamma, the emission always had the same energy: you could calculate the energy carried off by the particle emitted and compare it to the nucleus before and after, and everything added up according to Einstein's equation of E=mc². But something appeared to be seriously wrong with beta (electron) decay. Given a large collection of identical nuclei, the electrons emitted flew out with energies all over the map: from very low to an upper limit. This appeared to violate one of the most fundamental principles of physics: the conservation of energy. If the nucleus after plus the electron (including its kinetic energy) didn't add up to the energy of the nucleus before, where did the energy go? Few physicists were ready to abandon conservation of energy, but, after all, theory must ultimately conform to experiment, and if a multitude of precision measurements said that energy wasn't conserved in beta decay, maybe it really wasn't.

Fermi thought otherwise. In 1933, he proposed a theory of beta decay in which the emission of a beta particle (electron) from a nucleus was accompanied by emission of a particle he called a neutrino, which had been proposed earlier by Pauli. In one leap, Fermi introduced a third force, alongside gravity and electromagnetism, which could transform one particle into another, plus a new particle: without mass or charge, and hence extraordinarily difficult to detect, which nonetheless was responsible for carrying away the missing energy in beta decay. But Fermi did not just propose this mechanism in words: he presented a detailed mathematical theory of beta decay which made predictions for experiments which had yet to be performed. He submitted the theory in a paper to Nature in 1934. The editors rejected it, saying “it contained abstract speculations too remote from physical reality to be of interest to the reader.” This was quickly recognised and is now acknowledged as one of the most epic face-plants of peer review in theoretical physics. Fermi's theory rapidly became accepted as the correct model for beta decay. In 1956, the neutrino (actually, antineutrino) was detected with precisely the properties predicted by Fermi. This theory remained the standard explanation for beta decay until it was extended in the 1970s by the theory of the electroweak interaction, which is valid at higher energies than were available to experimenters in Fermi's lifetime.

Perhaps soured on theoretical work by the initial rejection of his paper on beta decay, Fermi turned to experimental exploration of the nucleus, using the newly-discovered particle, the neutron. Unlike alpha particles emitted by the decay of heavy elements like uranium and radium, neutrons had no electrical charge and could penetrate the nucleus of an atom without being repelled. Fermi saw this as the ideal probe to examine the nucleus, and began to use neutron sources to bombard a variety of elements to observe the results. One experiment directed neutrons at a target of silver and observed the creation of isotopes of silver when the neutrons were absorbed by the silver nuclei. But something very odd was happening: the results of the experiment seemed to differ when it was run on a laboratory bench with a marble top compared to one of wood. What was going on? Many people might have dismissed the anomaly, but Fermi had to know. He hypothesised that the probability a neutron would interact with a nucleus depended upon its speed (or, equivalently, energy): a slower neutron would effectively have more time to interact than one which whizzed through more rapidly. Neutrons which were reflected by the wood table top were “moderated” and had a greater probability of interacting with the silver target.

Fermi quickly tested this supposition by using paraffin wax and water as neutron moderators and measuring the dramatically increased probability of interaction (or as we would say today, neutron capture cross section) when neutrons were slowed down. This is fundamental to the design of nuclear reactors today. It was for this work that Fermi won the Nobel Prize in Physics for 1938.

By 1938, conditions for Italy's Jewish population had seriously deteriorated. Laura Fermi, despite her father's distinguished service as an admiral in the Italian navy, was now classified as a Jew, and therefore subject to travel restrictions, as were their two children. The Fermis went to their local Catholic parish, where they were (re-)married in a Catholic ceremony and their children baptised. With that paperwork done, the Fermi family could apply for passports and permits to travel to Stockholm to receive the Nobel prize. The Fermis locked their apartment, took a taxi, and boarded the train. Unbeknownst to the fascist authorities, they had no intention of returning.

Fermi had arranged an appointment at Columbia University in New York. His Nobel Prize award was US$45,000 (US$789,000 today). If he returned to Italy with the sum, he would have been forced to convert it to lire and then only be able to take the equivalent of US$50 out of the country on subsequent trips. Professor Fermi may not have been much interested in politics, but he could do arithmetic. The family went from Stockholm to Southampton, and then on an ocean liner to New York, with nothing other than their luggage, prize money, and, most importantly, freedom.

In his neutron experiments back in Rome, there had been curious results he and his colleagues never explained. When bombarding nuclei of uranium, the heaviest element then known, with neutrons moderated by paraffin wax, they had observed radioactive results which didn't make any sense. They expected to create new elements, heavier than uranium, but what they saw didn't agree with the expectations for such elements. Another mystery…in those heady days of nuclear physics, there was one wherever you looked. At just about the time Fermi's ship was arriving in New York, news arrived from Germany about what his group had observed, but not understood, four years before. Slow neutrons, which Fermi's group had pioneered, were able to split, or fission the nucleus of uranium into two lighter elements, releasing not only a large amount of energy, but additional neutrons which might be able to propagate the process into a “chain reaction”, producing either a large amount of energy or, perhaps, an enormous explosion.

As one of the foremost researchers in neutron physics, it was immediately apparent to Fermi that his new life in America was about to take a direction he'd never anticipated. By 1941, he was conducting experiments at Columbia with the goal of evaluating the feasibility of creating a self-sustaining nuclear reaction with natural uranium, using graphite as a moderator. In 1942, he was leading a project at the University of Chicago to build the first nuclear reactor. On December 2nd, 1942, Chicago Pile-1 went critical, producing all of half a watt of power. But the experiment proved that a nuclear chain reaction could be initiated and controlled, and it paved the way for both civil nuclear power and plutonium production for nuclear weapons. At the time he achieved one of the first major milestones of the Manhattan Project, Fermi's classification as an “enemy alien” had been removed only two months before. He and Laura Fermi did not become naturalised U.S. citizens until July of 1944.

Such was the breakneck pace of the Manhattan Project that even before the critical test of the Chicago pile, the DuPont company was already at work planning for the industrial scale production of plutonium at a facility which would eventually be built at the Hanford site near Richland, Washington. Fermi played a part in the design and commissioning of the X-10 Graphite Reactor in Oak Ridge, Tennessee, which served as a pathfinder and began operation in November, 1943, operating at a power level which was increased over time to 4 megawatts. This reactor produced the first substantial quantities of plutonium for experimental use, revealing the plutonium-240 contamination problem which necessitated the use of implosion for the plutonium bomb. Concurrently, he contributed to the design of the B Reactor at Hanford, which went critical in September 1944, running at 250 megawatts, that produced the plutonium for the Trinity test and the Fat Man bomb dropped on Nagasaki.

During the war years, Fermi divided his time among the Chicago research group, Oak Ridge, Hanford, and the bomb design and production group at Los Alamos. As General Leslie Groves, head of Manhattan Project, had forbidden the top atomic scientists from travelling by air, “Henry Farmer”, his wartime alias, spent much of his time riding the rails, accompanied by a bodyguard. As plutonium production ramped up, he increasingly spent his time with the weapon designers at Los Alamos, where Oppenheimer appointed him associate director and put him in charge of “Division F” (for Fermi), which acted as a consultant to all of the other divisions of the laboratory.

Fermi believed that while scientists could make major contributions to the war effort, how their work and the weapons they created were used were decisions which should be made by statesmen and military leaders. When appointed in May 1945 to the Interim Committee charged with determining how the fission bomb was to be employed, he largely confined his contributions to technical issues such as weapons effects. He joined Oppenheimer, Compton, and Lawrence in the final recommendation that “we can propose no technical demonstration likely to bring an end to the war; we see no acceptable alternative to direct military use.”

On July 16, 1945, Fermi witnessed the Trinity test explosion in New Mexico at a distance of ten miles from the shot tower. A few seconds after the blast, he began to tear little pieces of paper from from a sheet and drop them toward the ground. When the shock wave arrived, he paced out the distance it had blown them and rapidly computed the yield of the bomb as around ten kilotons of TNT. Nobody familiar with Fermi's reputation for making off-the-cuff estimates of physical phenomena was surprised that his calculation, done within a minute of the explosion, agreed within the margin of error with the actual yield of 20 kilotons, determined much later.

After the war, Fermi wanted nothing more than to return to his research. He opposed the continuation of wartime secrecy to postwar nuclear research, but, unlike some other prominent atomic scientists, did not involve himself in public debates over nuclear weapons and energy policy. When he returned to Chicago, he was asked by a funding agency simply how much money he needed. From his experience at Los Alamos he wanted both a particle accelerator and a big computer. By 1952, he had both, and began to produce results in scattering experiments which hinted at the new physics which would be uncovered throughout the 1950s and '60s. He continued to spend time at Los Alamos, and between 1951 and 1953 worked two months a year there, contributing to the hydrogen bomb project and analysis of Soviet atomic tests.

Everybody who encountered Fermi remarked upon his talents as an explainer and teacher. Seven of his students: six from Chicago and one from Rome, would go on to win Nobel Prizes in physics, in both theory and experiment. He became famous for posing “Fermi problems”, often at lunch, exercising the ability to make and justify order of magnitude estimates of difficult questions. When Freeman Dyson met with Fermi to present a theory he and his graduate students had developed to explain the scattering results Fermi had published, Fermi asked him how many free parameters Dyson had used in his model. Upon being told the number was four, he said, “I remember my old friend Johnny von Neumann used to say, with four parameters I can fit an elephant, and with five I can make him wiggle his trunk.” Chastened, Dyson soon concluded his model was a blind alley.

After returning from a trip to Europe in the fall of 1954, Fermi, who had enjoyed robust good health all his life, began to suffer from problems with digestion. Exploratory surgery found metastatic stomach cancer, for which no treatment was possible at the time. He died at home on November 28, 1954, two months past his fifty-third birthday. He had made a Fermi calculation of how long to rent the hospital bed in which he died: the rental expired two days after he did.

There was speculation that Fermi's life may have been shortened by his work with radiation, but there is no evidence of this. He was never exposed to unusual amounts of radiation in his work, and none of his colleagues, who did the same work at his side, experienced any medical problems.

This is a masterful biography of one of the singular figures in twentieth century science. The breadth of his interests and achievements is reflected in the list of things named after Enrico Fermi. Given the hyper-specialisation of modern science, it is improbable we will ever again see his like.

July 2017 

Smolin, Lee. The Trouble with Physics. New York: Houghton Mifflin, 2006. ISBN 0-618-55105-0.

The first forty years of the twentieth century saw a revolution in fundamental physics: special and general relativity changed our perception of space, time, matter, energy, and gravitation; quantum theory explained all of chemistry while wiping away the clockwork determinism of classical mechanics and replacing it with a deeply mysterious theory which yields fantastically precise predictions yet nobody really understands at its deepest levels; and the structure of the atom was elucidated, along with important clues to the mysteries of the nucleus. In the large, the universe was found to be enormously larger than expected and expanding—a dynamic arena which some suspected might have an origin and a future vastly different than its present state.

The next forty years worked out the structure and interactions of the particles and forces which constitute matter and govern its interactions, resulting in a standard model of particle physics with precisely defined theories which predicted all of the myriad phenomena observed in particle accelerators and in the highest energy events in the heavens. The universe was found to have originated in a big bang no more distant than three times the age of the Earth, and the birth cry of the universe had been detected by radio telescopes.

And then? Unexpected by almost all practitioners of high energy particle physics, which had become an enterprise larger by far than all of science at the start of the century, progress stopped. Since the wrapping up of the standard model around 1975, experiments have simply confirmed its predictions (with the exception of the discovery of neutrino oscillations and consequent mass, but that can be accommodated within the standard model without changing its structure), and no theoretical prediction of phenomena beyond the standard model has been confirmed experimentally.

What went wrong? Well, we certainly haven't reached the End of Science or even the End of Physics, because the theories which govern phenomena in the very small and very large—quantum mechanics and general relativity—are fundamentally incompatible with one another and produce nonsensical or infinite results when you attempt to perform calculations in the domain—known to exist from astronomical observations—where both must apply. Even a calculation as seemingly straightforward as estimating the energy of empty space yields a result which is 120 orders of magnitude greater than experiment shows it to be: perhaps the most embarrassing prediction in the history of science.

In the first chapter of this tour de force, physicist Lee Smolin poses “The Five Great Problems in Theoretical Physics”, all of which are just as mysterious today as they were thirty-five years ago. Subsequent chapters explore the origin and nature of these problems, and how it came to be, despite unprecedented levels of funding for theoretical and experimental physics, that we seem to be getting nowhere in resolving any of these fundamental enigmas.

This prolonged dry spell in high energy physics has seen the emergence of string theory (or superstring theory, or M-theory, or whatever they're calling it this year) as the dominant research program in fundamental physics. At the outset, there were a number of excellent reasons to believe that string theory pointed the way to a grand unification of all of the forces and particles of physics, and might answer many, if not all, of the Great Problems. This motivated many very bright people, including the author (who, although most identified with loop quantum gravity research, has published in string theory as well) to pursue this direction. What is difficult for an outsider to comprehend, however, is how a theoretical program which, after thirty-five years of intensive effort, has yet to make a single prediction testable by a plausible experiment; has failed to predict any of the major scientific surprises that have occurred over those years such as the accelerating expansion of the universe and the apparent variation in the fine structure constant; that does not even now exist in a well-defined mathematical form; and has not been rigorously proved to be a finite theory; has established itself as a virtual intellectual monopoly in the academy, forcing aspiring young theorists to work in string theory if they are to have any hope of finding a job, receiving grants, or obtaining tenure.

It is this phenomenon, not string theory itself, which, in the author's opinion, is the real “Trouble with Physics”. He considers string theory as quite possibly providing clues (though not the complete solution) to the great problems, and finds much to admire in many practitioners of this research. But monoculture is as damaging in academia as in agriculture, and when it becomes deeply entrenched in research institutions, squeezes out other approaches of equal or greater merit. He draws the distinction between “craftspeople”, who are good at performing calculations, filling in blanks, and extending an existing framework, and “seers”, who make the great intellectual leaps which create entirely new frameworks. After thirty-five years with no testable result, there are plenty of reasons to suspect a new framework is needed, yet our institutions select out those most likely to discover them, or force them to spend their most intellectually creative years doing tedious string theory calculations at the behest of their elders.

In the final chapters, Smolin looks at how academic science actually works today: how hiring and tenure decisions are made, how grant applications are evaluated, and the difficult career choices young physicists must make to work within this system. When reading this, the word “Gosplan” (Госпла́н) kept flashing through my mind, for the process he describes resembles nothing so much as central planning in a command economy: a small group of senior people, distant from the facts on the ground and the cutting edge of intellectual progress, trying to direct a grand effort in the interest of “efficiency”. But the lesson of more than a century of failed socialist experiments is that, in the timeless words of Rocket J. Squirrel, “that trick never works”—the decisions inevitably come down on the side of risk aversion, and are often influenced by cronyism and toadying to figures in authority. The concept of managing risk and reward by building a diversified portfolio of low and high risk placements which is second nature to managers of venture capital funds and industrial research and development laboratories appears to be totally absent in academic science, which is supposed to be working on the most difficult and fundamental questions. Central planning works abysmally for cement and steel manufacturing; how likely is it to spark the next scientific revolution?

There is much more to ponder: why string theory, as presently defined, cannot possibly be a complete theory which subsumes general relativity; hints from experiments which point to new physics beyond string theory; stories of other mathematically beautiful theories (such as SU(5) grand unification) which experiment showed to be dead wrong; and a candid view of the troubling groupthink, appeal to authority, and intellectual arrogance of some members of the string theory community. As with all of Smolin's writing, this is a joy to read, and you get the sense that he's telling you the straight story, as honestly as he can, not trying to sell you something. If you're interested in these issues, you'll probably also want to read Leonard Susskind's pro-string The Cosmic Landscape (March 2006) and Peter Woit's sceptical Not Even Wrong (June 2006).

September 2006 

Smolin, Lee. Time Reborn. New York: Houghton Mifflin, 2013. ISBN 978-0-547-51172-6.

Early in his career, the author received some unorthodox career advice from Richard Feynman. Feynman noted that in physics, as in all sciences, there were a large number of things that most professional scientists believed which nobody had been able to prove or demonstrate experimentally. Feynman's insight was that, when considering one of these problems as an area to investigate, there were two ways to approach it. The first was to try to do what everybody had failed previously to accomplish. This, he said, was extremely difficult and unlikely to succeed, since it assumes you're either smarter than everybody who has tried before or have some unique insight which eluded them. The other path is to assume that the failure of numerous brilliant people might indicate that what they were trying to demonstrate was, in fact, wrong, and that it might be wiser for the ambitious scientist to search for evidence to the contrary.

Based upon the author's previous work and publications, I picked up this book expecting a discussion of the problem of time in quantum gravity. What I found was something breathtakingly more ambitious. In essence, the author argues that when it comes to cosmology: the physics of the universe as a whole, physicists have been doing it wrong for centuries, and that what he calls the “Newtonian paradigm” must be replaced with one in which time is fundamental in order to stop speaking nonsense.

The equations of general relativity, especially when formulated in attempts to create a quantum theory of gravitation, seem to suggest that our perception of time is an illusion: we live in a timeless block universe, in which our consciousness can be thought of as a cursor moving through a fixed, deterministic spacetime. In general relativity, the rate of perceived flow of time depends upon one's state of motion and the amount of mass-energy in the vicinity of the observer, so it makes no sense to talk about any kind of global time co-ordinate. Quantum mechanics, on the other hand, assumes there is a global clock, external to the system and unaffected by it, which governs the evolution of the wave function. These views are completely incompatible—hence the problem of time in quantum gravity.

But the author argues that “timelessness” has its roots much deeper in the history and intellectual structure of physics. When one uses Newtonian mechanics to write down a differential equation which describes the path of a ball thrown upward, one is reducing a process which would otherwise require enumerating a list of positions and times to a timeless relationship which is valid over the entire trajectory. Time appears in the equation simply as a label which causes it to emit the position at that moment. The equation of motion, and, more importantly, the laws of motion which allow us to write it down for this particular case, are entirely timeless: they affect the object but are not affected by it, and they appear to be specified outside the system.

This, when you dare to step back and think about it, is distinctly odd. Where did these laws come from? Well, in Newton's day and in much of the history of science since, most scientists would say they were prescribed by a benevolent Creator. (My own view that they were put into the simulation by the 13 year old superkid who created it in order to win the Science Fair with the most interesting result, generating the maximum complexity, is isomorphic to this explanation.) Now, when you're analysing a system “in a box”, it makes perfect sense to assume the laws originate from outside and are fixed; after all, we can compare experiments run in different boxes and convince ourselves that the same laws obtain regardless of symmetries such as translation, orientation, or boost. But note that once we try to generalise this to the entire universe, as we must in cosmology, we run into a philosophical speed bump of singularity scale. Now we cannot escape the question of where the laws came from. If they're from inside the universe, then there must have been some dynamical process which created them. If they're outside the universe, they must have had to be imposed by some process which is external to the universe, which makes no sense if you define the universe as all there is.

Smolin suggests that laws exist within our universe, and that they evolve in an absolute time, which is primordial. There is no unmoved mover: the evolution of the universe (and the possibility that universes give birth to other universes) drives the evolution of the laws of physics. Perhaps the probabilistic results we observe in quantum mechanical processes are not built-in ahead of time and prescribed by timeless laws outside the universe, but rather a random choice from the results of previous similar measurements. This “principle of precedence”, which is remarkably similar to that of English common law, perfectly reproduces the results of most tests of quantum mechanics, but may be testable by precision experiments where circumstances never before created in the universe are measured, for example in quantum computing. (I am certain Prof. Smolin would advocate for my being beheaded were I to point out the similarity of this hypothesis with Rupert Sheldrake's concept of morphic resonance; some years ago I suggested to Dr Sheldrake a protein crystallisation experiment on the International Space Station to test this theory; it is real science, but to this date nobody has done it. Few wish to risk their careers testing what “everybody knows”.)

This is one those books you'll need to think about after you've read it, then after some time, re-read to get the most out of it. A collection of online appendices expand upon topics discussed in the book. An hour-long video discussion of the ideas in the book by the author and the intellectual path which led him to them is available.

June 2013 

Smolin, Lee. Einstein's Unfinished Revolution. New York: Penguin Press, 2019. ISBN 978-1-59420-619-1.

In the closing years of the nineteenth century, one of those nagging little discrepancies vexing physicists was the behaviour of the photoelectric effect. Originally discovered in 1887, the phenomenon causes certain metals, when illuminated by light, to absorb the light and emit electrons. The perplexing point was that there was a minimum wavelength (colour of light) necessary for electron emission, and for longer wavelengths, no electrons would be emitted at all, regardless of the intensity of the beam of light. For example, a certain metal might emit electrons when illuminated by green, blue, violet, and ultraviolet light, with the intensity of electron emission proportional to the light intensity, but red or yellow light, regardless of how intense, would not result in a single electron being emitted.

This didn't make any sense. According to Maxwell's wave theory of light, which was almost universally accepted and had passed stringent experimental tests, the energy of light depended upon the amplitude of the wave (its intensity), not the wavelength (or, reciprocally, its frequency). And yet the photoelectric effect didn't behave that way—it appeared that whatever was causing the electrons to be emitted depended on the wavelength of the light, and what's more, there was a sharp cut-off below which no electrons would be emitted at all.

In 1905, in one of his “miracle year” papers, “On a Heuristic Viewpoint Concerning the Production and Transformation of Light”, Albert Einstein suggested a solution to the puzzle. He argued that light did not propagate as a wave at all, but rather in discrete particles, or “quanta”, later named “photons”, whose energy was proportional to the wavelength of the light. This neatly explained the behaviour of the photoelectric effect. Light with a wavelength longer than the cut-off point was transmitted by photons whose energy was too low to knock electrons out of metal they illuminated, while those above the threshold could liberate electrons. The intensity of the light was a measure of the number of photons in the beam, unrelated to the energy of the individual photons.

This paper became one of the cornerstones of the revolutionary theory of quantum mechanics, the complete working out of which occupied much of the twentieth century. Quantum mechanics underlies the standard model of particle physics, which is arguably the most thoroughly tested theory in the history of physics, with no experiment showing results which contradict its predictions since it was formulated in the 1970s. Quantum mechanics is necessary to explain the operation of the electronic and optoelectronic devices upon which our modern computing and communication infrastructure is built, and describes every aspect of physical chemistry.

But quantum mechanics is weird. Consider: if light consists of little particles, like bullets, then why when you shine a beam of light on a barrier with two slits do you get an interference pattern with bright and dark bands precisely as you get with, say, water waves? And if you send a single photon at a time and try to measure which slit it went through, you find it always went through one or the other, but then the interference pattern goes away. It seems like whether the photon behaves as a wave or a particle depends upon how you look at it. If you have an hour, here is grand master explainer Richard Feynman (who won his own Nobel Prize in 1965 for reconciling the quantum mechanical theory of light and the electron with Einstein's special relativity) exploring how profoundly weird the double slit experiment is.

Fundamentally, quantum mechanics seems to violate the principle of realism, which the author defines as follows.

The belief that there is an objective physical world whose properties are independent of what human beings know or which experiments we choose to do. Realists also believe that there is no obstacle in principle to our obtaining complete knowledge of this world.

This has been part of the scientific worldview since antiquity and yet quantum mechanics, confirmed by innumerable experiments, appears to indicate we must abandon it. Quantum mechanics says that what you observe depends on what you choose to measure; that there is an absolute limit upon the precision with which you can measure pairs of properties (for example position and momentum) set by the uncertainty principle; that it isn't possible to predict the outcome of experiments but only the probability among a variety of outcomes; and that particles which are widely separated in space and time but which have interacted in the past are entangled and display correlations which no classical mechanistic theory can explain—Einstein called the latter “spooky action at a distance”. Once again, all of these effects have been confirmed by precision experiments and are not fairy castles erected by theorists.

From the formulation of the modern quantum theory in the 1920s, often called the Copenhagen interpretation after the location of the institute where one of its architects, Neils Bohr, worked, a number of eminent physicists including Einstein and Louis de Broglie were deeply disturbed by its apparent jettisoning of the principle of realism in favour of what they considered a quasi-mystical view in which the act of “measurement” (whatever that means) caused a physical change (wave function collapse) in the state of a system. This seemed to imply that the photon, or electron, or anything else, did not have a physical position until it interacted with something else: until then it was just an immaterial wave function which filled all of space and (when squared) gave the probability of finding it at that location.

In 1927, de Broglie proposed a pilot wave theory as a realist alternative to the Copenhagen interpretation. In the pilot wave theory there is a real particle, which has a definite position and momentum at all times. It is guided in its motion by a pilot wave which fills all of space and is defined by the medium through which it propagates. We cannot predict the exact outcome of measuring the particle because we cannot have infinitely precise knowledge of its initial position and momentum, but in principle these quantities exist and are real. There is no “measurement problem” because we always detect the particle, not the pilot wave which guides it. In its original formulation, the pilot wave theory exactly reproduced the predictions of the Copenhagen formulation, and hence was not a competing theory but rather an alternative interpretation of the equations of quantum mechanics. Many physicists who preferred to “shut up and calculate” considered interpretations a pointless exercise in phil-oss-o-phy, but de Broglie and Einstein placed great value on retaining the principle of realism as a cornerstone of theoretical physics. Lee Smolin sketches an alternative reality in which “all the bright, ambitious students flocked to Paris in the 1930s to follow de Broglie, and wrote textbooks on pilot wave theory, while Bohr became a footnote, disparaged for the obscurity of his unnecessary philosophy”. But that wasn't what happened: among those few physicists who pondered what the equations meant about how the world really works, the Copenhagen view remained dominant.

In the 1950s, independently, David Bohm invented a pilot wave theory which he developed into a complete theory of nonrelativistic quantum mechanics. To this day, a small community of “Bohmians” continue to explore the implications of his theory, working on extending it to be compatible with special relativity. From a philosophical standpoint the de Broglie-Bohm theory is unsatisfying in that it involves a pilot wave which guides a particle, but upon which the particle does not act. This is an “unmoved mover”, which all of our experience of physics argues does not exist. For example, Newton's third law of motion holds that every action has an equal and opposite reaction, and in Einstein's general relativity, spacetime tells mass-energy how to move while mass-energy tells spacetime how to curve. It seems odd that the pilot wave could be immune from influence of the particle it guides. A few physicists, such as Jack Sarfatti, have proposed “post-quantum” extensions to Bohm's theory in which there is back-reaction from the particle on the pilot wave, and argue that this phenomenon might be accessible to experimental tests which would distinguish post-quantum phenomena from the predictions of orthodox quantum mechanics. A few non-physicist crackpots have suggested these phenomena might even explain flying saucers.

Moving on from pilot wave theory, the author explores other attempts to create a realist interpretation of quantum mechanics: objective collapse of the wave function, as in the Penrose interpretation; the many worlds interpretation (which Smolin calls “magical realism”); and decoherence of the wavefunction due to interaction with the environment. He rejects all of them as unsatisfying, because they fail to address glaring lacunæ in quantum theory which are apparent from its very equations.

The twentieth century gave us two pillars of theoretical physics: quantum mechanics and general relativity—Einstein's geometric theory of gravitation. Both have been tested to great precision, but they are fundamentally incompatible with one another. Quantum mechanics describes the very small: elementary particles, atoms, and molecules. General relativity describes the very large: stars, planets, galaxies, black holes, and the universe as a whole. In the middle, where we live our lives, neither much affects the things we observe, which is why their predictions seem counter-intuitive to us. But when you try to put the two theories together, to create a theory of quantum gravity, the pieces don't fit. Quantum mechanics assumes there is a universal clock which ticks at the same rate everywhere in the universe. But general relativity tells us this isn't so: a simple experiment shows that a clock runs slower when it's in a gravitational field. Quantum mechanics says that it isn't possible to determine the position of a particle without its interacting with another particle, but general relativity requires the knowledge of precise positions of particles to determine how spacetime curves and governs the trajectories of other particles. There are a multitude of more gnarly and technical problems in what Stephen Hawking called “consummating the fiery marriage between quantum mechanics and general relativity”. In particular, the equations of quantum mechanics are linear, which means you can add together two valid solutions and get another valid solution, while general relativity is nonlinear, where trying to disentangle the relationships of parts of the systems quickly goes pear-shaped and many of the mathematical tools physicists use to understand systems (in particular, perturbation theory) blow up in their faces.

Ultimately, Smolin argues, giving up realism means abandoning what science is all about: figuring out what is really going on. The incompatibility of quantum mechanics and general relativity provides clues that there may be a deeper theory to which both are approximations that work in certain domains (just as Newtonian mechanics is an approximation of special relativity which works when velocities are much less than the speed of light). Many people have tried and failed to “quantise general relativity”. Smolin suggests the problem is that quantum theory itself is incomplete: there is a deeper theory, a realistic one, to which our existing theory is only an approximation which works in the present universe where spacetime is nearly flat. He suggests that candidate theories must contain a number of fundamental principles. They must be background independent, like general relativity, and discard such concepts as fixed space and a universal clock, making both dynamic and defined based upon the components of a system. Everything must be relational: there is no absolute space or time; everything is defined in relation to something else. Everything must have a cause, and there must be a chain of causation for every event which traces back to its causes; these causes flow only in one direction. There is reciprocity: any object which acts upon another object is acted upon by that object. Finally, there is the “identity of indescernibles”: two objects which have exactly the same properties are the same object (this is a little tricky, but the idea is that if you cannot in some way distinguish two objects [for example, by their having different causes in their history], then they are the same object).

This argues that what we perceive, at the human scale and even in our particle physics experiments, as space and time are actually emergent properties of something deeper which was manifest in the early universe and in extreme conditions such as gravitational collapse to black holes, but hidden in the bland conditions which permit us to exist. Further, what we believe to be “laws” and “constants” may simply be precedents established by the universe as it tries to figure out how to handle novel circumstances. Just as complex systems like markets and evolution in ecosystems have rules that change based upon events within them, maybe the universe is “making it up as it goes along”, and in the early universe, far from today's near-equilibrium, wild and crazy things happened which may explain some of the puzzling properties of the universe we observe today.

This needn't forever remain in the realm of speculation. It is easy, for example, to synthesise a protein which has never existed before in the universe (it's an example of a combinatorial explosion). You might try, for example, to crystallise this novel protein and see how difficult it is, then try again later and see if the universe has learned how to do it. To be extra careful, do it first on the International Space Station and then in a lab on the Earth. I suggested this almost twenty years ago as a test of Rupert Sheldrake's theory of morphic resonance, but (although doubtless Smolin would shun me for associating his theory with that one), it might produce interesting results.

The book concludes with a very personal look at the challenges facing a working scientist who has concluded the paradigm accepted by the overwhelming majority of his or her peers is incomplete and cannot be remedied by incremental changes based upon the existing foundation. He notes:

There is no more reasonable bet than that our current knowledge is incomplete. In every era of the past our knowledge was incomplete; why should our period be any different? Certainly the puzzles we face are at least as formidable as any in the past. But almost nobody bets this way. This puzzles me.

Well, it doesn't puzzle me. Ever since I learned classical economics, I've always learned to look at the incentives in a system. When you regard academia today, there is huge risk and little reward to get out a new notebook, look at the first blank page, and strike out in an entirely new direction. Maybe if you were a twenty-something patent examiner in a small city in Switzerland in 1905 with no academic career or reputation at risk you might go back to first principles and overturn space, time, and the wave theory of light all in one year, but today's institutional structure makes it almost impossible for a young researcher (and revolutionary ideas usually come from the young) to strike out in a new direction. It is a blessing that we have deep thinkers such as Lee Smolin setting aside the easy path to retirement to ask these deep questions today.

Here is a lecture by the author at the Perimeter Institute about the topics discussed in the book. He concentrates mostly on the problems with quantum theory and not the speculative solutions discussed in the latter part of the book.

May 2019 

Smyth, Henry D. Atomic Energy for Military Purposes. Stanford, CA, Stanford University Press, [1945] 1990. ISBN 978-0-8047-1722-9.

This document was released to the general public by the United States War Department on August 12th, 1945, just days after nuclear weapons had been dropped on Japan (Hiroshima on August 6th and Nagasaki on August 9th). The author, Prof. Henry D. Smyth of Princeton University, had worked on the Manhattan Project since early 1941, was involved in a variety of theoretical and practical aspects of the effort, and possessed security clearances which gave him access to all of the laboratories and production facilities involved in the project. In May, 1944, Smyth, who had suggested such a publication, was given the go ahead by the Manhattan Project's Military Policy Committee to prepare an unclassified summary of the bomb project. This would have a dual purpose: to disclose to citizens and taxpayers what had been done on their behalf, and to provide scientists and engineers involved in the project a guide to what they could discuss openly in the postwar period: if it was in the “Smyth Report” (as it came to be called), it was public information, otherwise mum's the word.

The report is a both an introduction to the physics underlying nuclear fission and its use in both steady-state reactors and explosives, production of fissile material (both separation of reactive Uranium-235 from the much more abundant Uranium-238 and production of Plutonium-239 in nuclear reactors), and the administrative history and structure of the project. Viewed as a historical document, the report is as interesting in what it left out as what was disclosed. Essentially none of the key details discovered and developed by the Manhattan Project which might be of use to aspiring bomb makers appear here. The key pieces of information which were not known to interested physicists in 1940 before the curtain of secrecy descended upon anything related to nuclear fission were inherently disclosed by the very fact that a fission bomb had been built, detonated, and produced a very large explosive yield.

• It was possible to achieve a fast fission reaction with substantial explosive yield.
• It was possible to prepare a sufficient quantity of fissile material (uranium or plutonium) to build a bomb.
• The critical mass required by a bomb was within the range which could be produced by a country with the industrial resources of the United States and small enough that it could be delivered by an aircraft.

None of these were known at the outset of the Manhattan Project (which is why it was such a gamble to undertake it), but after the first bombs were used, they were apparent to anybody who was interested, most definitely including the Soviet Union (who, unbeknownst to Smyth and the political and military leaders of the Manhattan Project, already had the blueprints for the Trinity bomb and extensive information on all aspects of the project from their spies.)

Things never disclosed in the Smyth Report include the critical masses of uranium and plutonium, the problem of contamination of reactor-produced plutonium with the Plutonium-240 isotope and the consequent impossibility of using a gun-type design with plutonium, the technique of implosion and the technologies required to achieve it such as explosive lenses and pulsed power detonators (indeed, the word “implosion” appears nowhere in the document), and the chemical processes used to separate plutonium from uranium and fission products irradiated in a production reactor. In many places, it is explicitly said that military security prevents discussion of aspects of the project, but in others nasty surprises which tremendously complicated the effort are simply not mentioned—left for others wishing to follow in its path to discover for themselves.

Reading the first part of the report, you get the sense that it had not yet been decided whether to disclose the existence or scale of the Los Alamos operation. Only toward the end of the work is Los Alamos named and the facilities and tasks undertaken there described. The bulk of the report was clearly written before the Trinity test of the plutonium bomb on July 16, 1945. It is described in an appendix which reproduces verbatim the War Department press release describing the test, which was only issued after the bombs were used on Japan.

This document is of historical interest only. If you're interested in the history of the Manhattan Project and the design of the first fission bombs, more recent works such as Richard Rhodes' The Making of the Atomic Bomb are much better sources. For those aware of the scope and details of the wartime bomb project, the Smyth report is an interesting look at what those responsible for it felt comfortable disclosing and what they wished to continue to keep secret. The forward by General Leslie R. Groves reminds readers that “Persons disclosing or securing additional information by any means whatsoever without authorization are subject to severe penalties under the Espionage Act.”

I read a Kindle edition from another publisher which is much less expensive than the Stanford paperback but contains a substantial number of typographical errors probably introduced by scanning a paper source document with inadequate subsequent copy editing.

November 2019 

Staley, Kent W. The Evidence for the Top Quark. Cambridge: Cambridge University Press, 2004. ISBN 0-521-82710-8.

A great deal of nonsense and intellectual nihilism has been committed in the name of “science studies”. Here, however, is an exemplary volume which shows not only how the process of scientific investigation should be studied, but also why. The work is based on the author's dissertation in philosophy, which explored the process leading to the September 1994 publication of the “Evidence for top quark production in pp collisions at √s = 1.8 TeV” paper in Physical Review D. This paper is a quintessential example of Big Science: more than four hundred authors, sixty pages of intricate argumentation from data produced by a detector weighing more than two thousand tons, and automated examination of millions and millions of collisions between protons and antiprotons accelerated to almost the speed of light by the Tevatron, all to search, over a period of months, for an elementary particle which cannot be observed in isolation, and finally reporting “evidence” for its existence (but not “discovery” or “observation”) based on a total of just twelve events “tagged” by three different algorithms, when a total of about 5.7 events would have been expected due to other causes (“background”) purely by chance alone.

Through extensive scrutiny of contemporary documents and interviews with participants in the collaboration which performed the experiment, the author provides a superb insight into how science on this scale is done, and the process by which the various kinds of expertise distributed throughout a large collaboration come together to arrive at the consensus they have found something worthy of publication. He explores the controversies about the paper both within the collaboration and subsequent to its publication, and evaluates claims that choices made by the experimenters may have a produced a bias in the results, and/or that choosing experimental “cuts” after having seen data from the detector might constitute “tuning on the signal”: physicist-speak for choosing the criteria for experimental success after having seen the results from the experiment, a violation of the “predesignation” principle usually assumed in statistical tests.

In the final two, more philosophical, chapters, the author introduces the concept of “Error-Statistical Evidence”, and evaluates the analysis in the “Evidence” paper in those terms, concluding that despite all the doubt and controversy, the decision making process was, in the end, ultimately objective. (And, of course, subsequent experimentation has shown the information reported in the Evidence paper to be have been essentially correct.)

Popular accounts of high energy physics sometimes gloss over the fantastically complicated and messy observations which go into a reported result to such an extent you might think experimenters are just waiting around looking at a screen waiting for a little ball to pop out with a “t” or whatever stencilled on the side. This book reveals the subtlety of the actual data from these experiments, and the intricate chain of reasoning from the multitudinous electronic signals issuing from a particle detector to the claim of having discovered a new particle. This is not, however, remotely a work of popularisation. While attempting to make the physics accessible to philosophers of science and the philosophy comprehensible to physicists, each will find the portions outside their own speciality tough going. A reader without a basic understanding of the standard model of particle physics and the principles of statistical hypothesis testing will probably end up bewildered and may not make it to the end, but those who do will be rewarded with a detailed understanding of high energy particle physics experiments and the operation of large collaborations of researchers which is difficult to obtain anywhere else.

August 2006 

Stenhoff, Mark. Ball Lightning. New York: Kluwer Academic / Plenum Publishers, 1999. ISBN 0-306-46150-1.

Reports of ball lightning—glowing spheres of light which persist for some number of seconds, usually associated with cloud to ground lightning strikes during thunderstorms, date back to the classical Greeks. Since 1838, when physicist and astronomer Dominique Arago published a survey of twenty reports of ball lightning, a long list of scientists, many eminent, have tried their hands at crafting a theory which might explain such an odd phenomenon yet, at the start of the twenty-first century ball lightning remains, as Arago said in 1854, “One of the most inexplicable problems of physics today.”

Well, actually, ball lightning only poses problems to the physics of yesterday and today if it, you know, exists, and the evidence that it does is rather weak, as this book demonstrates. (Its author does come down in favour of the existence of ball lightning, and wrote the 1976 Nature paper which helped launched the modern study of the phenomenon.) As of the date this book was published, not a single unambiguous photograph, movie, or video recording of ball lightning was known to exist, and most of the “classic” photographs illustrated in chapter 9 are obvious fakes created by camera motion and double exposure. It is also difficult when dealing with reports by observers unacquainted with the relevant phenomena to sort out genuine ball lightning (if such exists) from other well-documented and understood effects such as corona discharges (St. Elmo's fire), that perennial favourite of UFO debunkers: ignis fatuus or swamp gas, and claims of damage caused by the passage of ball lightning or its explosive dissipation from those produced by conventional lightning strikes. See the author's re-casting of a lightning strike to a house which he personally investigated into “ball lightning language” on pp. 105–106 for an example of how such reports can originate.

Still, after sorting out the mis-identifications, hoaxes, and other dross, a body of reports remains, some by expert observers of atmospheric phenomena, which have a consistency not to be found, for example, in UFO reports. A number of observations of ball lightning within metallic aircraft fuselages are almost identical and pose a formidable challenge to most models. The absence of unambiguous evidence has not in any way deterred the theoretical enterprise, and chapters 11–13 survey models based on, among other mechanisms, heated air, self-confining plasma vortices and spheroids, radial charge separation, chemical reactions and combustion, microwave excitation of metastable molecules of atmospheric gases, nuclear fusion and the production of unstable isotopes of oxygen and nitrogen, focusing of cosmic rays, antimatter meteorites, and microscopic black holes. One does not get the sense of this converging upon a consensus. Among the dubious theories, there are some odd claims of experimental results such as the production of self-sustaining plasma balls by placing a short burning candle in a kitchen microwave oven (didn't work for me, anyway—if you must try it yourself, please use common sense and be careful), and reports of producing ball lightning sustained by fusion of deuterium in atmospheric water vapour by short circuiting a 200 tonne submarine accumulator battery. (Don't try this one at home, kids!)

The book concludes with the hope that with increasing interest in ball lightning, as evidenced by conferences such as the International Symposia on Ball Lightning, and additional effort in collecting and investigating reports, this centuries-old puzzle may be resolved within this decade. I'm not so sure—the UFO precedent does not incline one to optimism. For those motivated to pursue the matter further, a bibliography of more than 75 pages and 2400 citations is included.

June 2005 

Susskind, Leonard. The Cosmic Landscape. New York: Little, Brown, 2006. ISBN 0-316-15579-9.

Leonard Susskind (and, independently, Yoichiro Nambu) co-discovered the original hadronic string theory in 1969. He has been a prominent contributor to a wide variety of topics in theoretical physics over his long career, and is a talented explainer of abstract theoretical concepts to the general reader. This book communicates both the physics and cosmology of the “string landscape” (a term he coined in 2003) revolution which has swiftly become the consensus among string theorists, as well as the intellectual excitement of those exploring this new frontier.

The book is subtitled “String Theory and the Illusion of Intelligent Design” which may be better marketing copy—controversy sells—than descriptive of the contents. There is very little explicit discussion of intelligent design in the book at all except in the first and last pages, and what is meant by “intelligent design” is not what the reader might expect: design arguments in the origin and evolution of life, but rather the apparent fine-tuning of the physical constants of our universe, the cosmological constant in particular, without which life as we know it (and, in many cases, not just life but even atoms, stars, and galaxies) could not exist. Susskind is eloquent in describing why the discovery that the cosmological constant, which virtually every theoretical physicist would have bet had to be precisely zero, is (apparently) a small tiny positive number, seemingly fine tuned to one hundred and twenty decimal places “hit us like the proverbial ton of bricks” (p. 185)—here was a number which, not only did theory suggest should be 120 orders of magnitude greater, but which, had it been slightly larger than its minuscule value, would have precluded structure formation (and hence life) in the universe. One can imagine some as-yet-undiscovered mathematical explanation why a value is precisely zero (and, indeed, physicists did: it's called supersymmetry, and searching for evidence of it is one of the reasons they're spending billions of taxpayer funds to build the Large Hadron Collider), but when you come across a dial set with the almost ridiculous precision of 120 decimal places and it's a requirement for our own existence, thoughts of a benevolent Creator tend to creep into the mind of even the most doctrinaire scientific secularist. This is how the appearance of “intelligent design” (as the author defines it) threatens to get into the act, and the book is an exposition of the argument string theorists and cosmologists have developed to contend that such apparent design is entirely an illusion.

The very title of the book, then invites us to contrast two theories of the origin of the universe: “intelligent design” and the “string landscape”. So, let's accept that challenge and plunge right in, shall we? First of all, permit me to observe that despite frequent claims to the contrary, including some in this book, intelligent design need not presuppose a supernatural being operating outside the laws of science and/or inaccessible to discovery through scientific investigation. The origin of life on Earth due to deliberate seeding with engineered organisms by intelligent extraterrestrials is a theory of intelligent design which has no supernatural component, evidence of which may be discovered by science in the future, and which is sufficiently plausible to have persuaded Francis Crick, co-discoverer of the structure of DNA, was the most likely explanation. If you observe a watch, you're entitled to infer the existence of a watchmaker, but there's no reason to believe he's a magician, just a craftsman.

If we're to compare these theories, let us begin by stating them both succinctly:

Theory 1: Intelligent Design.   An intelligent being created the universe and chose the initial conditions and physical laws so as to permit the existence of beings like ourselves.

Theory 2: String Landscape.   The laws of physics and initial conditions of the universe are chosen at random from among 10⁵⁰⁰ possibilities, only a vanishingly small fraction of which (probably no more than one in 10¹²⁰) can support life. The universe we observe, which is infinite in extent and may contain regions where the laws of physics differ, is one of an infinite number of causally disconnected “pocket universes“ which spontaneously form from quantum fluctuations in the vacuum of parent universes, a process which has been occurring for an infinite time in the past and will continue in the future, time without end. Each of these pocket universes which, together, make up the “megaverse”, has its own randomly selected laws of physics, and hence the overwhelming majority are sterile. We find ourselves in one of the tiny fraction of hospitable universes because if we weren't in such an exceptionally rare universe, we wouldn't exist to make the observation. Since there are an infinite number of universes, however, every possibility not only occurs, but occurs an infinite number of times, so not only are there an infinite number of inhabited universes, there are an infinite number identical to ours, including an infinity of identical copies of yourself wondering if this paragraph will ever end. Not only does the megaverse spawn an infinity of universes, each universe itself splits into two copies every time a quantum measurement occurs. Our own universe will eventually spawn a bubble which will destroy all life within it, probably not for a long, long time, but you never know. Evidence for all of the other universes is hidden behind a cosmic horizon and may remain forever inaccessible to observation.

Paging Friar Ockham! If unnecessarily multiplying hypotheses are stubble indicating a fuzzy theory, it's pretty clear which of these is in need of the razor! Further, while one can imagine scientific investigation discovering evidence for Theory 1, almost all of the mechanisms which underlie Theory 2 remain, barring some conceptual breakthrough equivalent to looking inside a black hole, forever hidden from science by an impenetrable horizon through which no causal influence can propagate. So severe is this problem that chapter 9 of the book is devoted to the question of how far theoretical physics can go in the total absence of experimental evidence. What's more, unlike virtually every theory in the history of science, which attempted to describe the world we observe as accurately and uniquely as possible, Theory 2 predicts every conceivable universe and says, hey, since we do, after all, inhabit a conceivable universe, it's consistent with the theory. To one accustomed to the crystalline inevitability of Newtonian gravitation, general relativity, quantum electrodynamics, or the laws of thermodynamics, this seems by comparison like a California blonde saying “whatever”—the cosmology of despair.

Scientists will, of course, immediately rush to attack Theory 1, arguing that a being such as that it posits would necessarily be “indistinguishable from magic”, capable of explaining anything, and hence unfalsifiable and beyond the purview of science. (Although note that on pp. 192–197 Susskind argues that Popperian falsifiability should not be a rigid requirement for a theory to be deemed scientific. See Lee Smolin's Scientific Alternatives to the Anthropic Principle for the argument against the string landscape theory on the grounds of falsifiability, and the 2004 Smolin/Susskind debate for a more detailed discussion of this question.) But let us look more deeply at the attributes of what might be called the First Cause of Theory 2. It not only permeates all of our universe, potentially spawning a bubble which may destroy it and replace it with something different, it pervades the abstract landscape of all possible universes, populating them with an infinity of independent and diverse universes over an eternity of time: omnipresent in spacetime. When a universe is created, all the parameters which ultimately govern its ultimate evolution (under the probabilistic laws of quantum mechanics, to be sure) are fixed at the moment of creation: omnipotent to create any possibility, perhaps even varying the mathematical structures underlying the laws of physics. As a budded off universe evolves, whether a sterile formless void or teeming with intelligent life, no information is ever lost in its quantum evolution, not even down a black hole or across a cosmic horizon, and every quantum event splits the universe and preserves all possible outcomes. The ensemble of universes is thus omniscient of all its contents. Throw in intelligent and benevolent, and you've got the typical deity, and since you can't observe the parallel universes where the action takes place, you pretty much have to take it on faith. Where have we heard that before?

Lest I be accused of taking a cheap shot at string theory, or advocating a deistic view of the universe, consider the following creation story which, after John A. Wheeler, I shall call “Creation without the Creator”. Many extrapolations of continued exponential growth in computing power envision a technological singularity in which super-intelligent computers designing their own successors rapidly approach the ultimate physical limits on computation. Such computers would be sufficiently powerful to run highly faithful simulations of complex worlds, including intelligent beings living within them which need not be aware they were inhabiting a simulation, but thought they were living at the “top level”, who eventually passed through their own technological singularity, created their own simulated universes, populated them with intelligent beings who, in turn,…world without end. Of course, each level of simulation imposes a speed penalty (though, perhaps not much in the case of quantum computation), but it's not apparent to the inhabitants of the simulation since their own perceived time scale is in units of the “clock rate” of the simulation.

If an intelligent civilisation develops to the point where it can build these simulated universes, will it do so? Of course it will—just look at the fascination crude video game simulations have for people today. Now imagine a simulation as rich as reality and unpredictable as tomorrow, actually creating an inhabited universe—who could resist? As unlimited computing power becomes commonplace, kids will create innovative universes and evolve them for billions of simulated years for science fair projects. Call the mean number of simulated universes created by intelligent civilisations in a given universe (whether top-level or itself simulated) the branching factor. If this is greater than one, and there is a single top-level non-simulated universe, then it will be outnumbered by simulated universes which grow exponentially in numbers with the depth of the simulation. Hence, by the Copernican principle, or principle of mediocrity, we should expect to find ourselves in a simulated universe, since they vastly outnumber the single top-level one, which would be an exceptional place in the ensemble of real and simulated universes. Now here's the point: if, as we should expect from this argument, we do live in a simulated universe, then our universe is the product of intelligent design and Theory 1 is an absolutely correct description of its origin.

Suppose this is the case: we're inside a simulation designed by a freckle-faced superkid for extra credit in her fifth grade science class. Is this something we could discover, or must it, like so many aspects of Theory 2, be forever hidden from our scientific investigation? Surprisingly, this variety of Theory 1 is quite amenable to experiment: neither revelation nor faith is required. What would we expect to see if we inhabited a simulation? Well, there would probably be a discrete time step and granularity in position fixed by the time and position resolution of the simulation—check, and check: the Planck time and distance appear to behave this way in our universe. There would probably be an absolute speed limit to constrain the extent we could directly explore and impose a locality constraint on propagating updates throughout the simulation—check: speed of light. There would be a limit on the extent of the universe we could observe—check: the Hubble radius is an absolute horizon we cannot penetrate, and the last scattering surface of the cosmic background radiation limits electromagnetic observation to a still smaller radius. There would be a limit on the accuracy of physical measurements due to the finite precision of the computation in the simulation—check: Heisenberg uncertainty principle—and, as in games, randomness would be used as a fudge when precision limits were hit—check: quantum mechanics.

Might we expect surprises as we subject our simulated universe to ever more precise scrutiny, perhaps even astonishing the being which programmed it with our cunning and deviousness (as the author of any software package has experienced at the hands of real-world users)? Who knows, we might run into round-off errors which “hit us like a ton of bricks”! Suppose there were some quantity, say, that was supposed to be exactly zero but, if you went and actually measured the geometry way out there near the edge and crunched the numbers, you found out it differed from zero in the 120th decimal place. Why, you might be as shocked as the naïve Perl programmer who ran the program “printf("%.18f", 0.2)” and was aghast when it printed “0.200000000000000011” until somebody explained that with about 56 bits of mantissa in IEEE double precision floating point, you only get about 17 decimal digits (log₁₀ 2⁵⁶) of precision. So, what does a round-off in the 120th digit imply? Not Theory 2, with its infinite number of infinitely reproducing infinite universes, but simply that our Theory 1 intelligent designer used 400 bit numbers (log₂ 10¹²⁰) in the simulation and didn't count on our noticing—remember you heard it here first, and if pointing this out causes the simulation to be turned off, sorry about that, folks! Surprises from future experiments which would be suggestive (though not probative) that we're in a simulated universe would include failure to find any experimental signature of quantum gravity (general relativity could be classical in the simulation, since potential conflicts with quantum mechanics would be hidden behind event horizons in the present-day universe, and extrapolating backward to the big bang would be meaningless if the simulation were started at a later stage, say at the time of big bang nucleosynthesis), and discovery of limits on the ability to superpose wave functions for quantum computation which could result from limited precision in the simulation as opposed to the continuous complex values assumed by quantum mechanics. An interesting theoretical program would be to investigate feasible experiments which, by magnifying physical effects similar to proposed searches for quantum gravity signals, would detect round-off errors of magnitude comparable to the cosmological constant.

But seriously, this is an excellent book and anybody who's interested in the strange direction in which the string theorists are veering these days ought to read it; it's well-written, authoritative, reasonably fair to opposing viewpoints (although I'm surprised the author didn't address the background spacetime criticism of string theory raised so eloquently by Lee Smolin), and provides a roadmap of how string theory may develop in the coming years. The only nagging question you're left with after finishing the book is whether after thirty years of theorising which comes to the conclusion that everything is predicted and nothing can be observed, it's about science any more.

March 2006 

Susskind, Leonard. The Black Hole War. New York: Little, Brown, 2008. ISBN 978-0-316-01640-7.

I hesitated buying this book for some months after its publication because of a sense there was something “off” in the author's last book, The Cosmic Landscape (March 2006). I should learn to trust my instincts more; this book treats a fascinating and important topic on the wild frontier between general relativity and quantum mechanics in a disappointing, deceptive, and occasionally infuriating manner.

The author is an eminent physicist who has made major contributions to string theory, the anthropic string landscape, and the problem of black hole entropy and the fate of information which is swallowed by a black hole. The latter puzzle is the topic of the present book, which is presented as a “war” between Stephen Hawking and his followers, mostly general relativity researchers, and Susskind and his initially small band of quantum field and string theorists who believed that information must be preserved in black hole accretion and evaporation lest the foundations of physics (unitarity and the invertibility of the S-matrix) be destroyed.

Here is a simple way to understand one aspect of this apparent paradox. Entropy is a measure of the hidden information in a system. The entropy of gas at equilibrium is very high because there are a huge number of microscopic configurations (position and velocity) of the molecules of the gas which result in the same macroscopic observables: temperature, pressure, and volume. A perfect crystal at absolute zero, on the other hand, has (neglecting zero-point energy), an entropy of zero because there is precisely one arrangement of atoms which exactly reproduces it. A classical black hole, as described by general relativity, is characterised by just three parameters: mass, angular momentum, and electrical charge. (The very same basic parameters as elementary particles—hmmmm….) All of the details of the mass and energy which went into the black hole: lepton and baryon number, particle types, excitations, and higher level structure are lost as soon as they cross the event horizon and cause it to expand. According to Einstein's theory, two black holes with the same mass, spin, and charge are absolutely indistinguishable even if the first was made from the collapse of a massive star and the second by crushing 1975 Ford Pintos in a cosmic trash compactor. Since there is a unique configuration for a given black hole, there is no hidden information and its entropy should therefore be zero.

But consider this: suppose you heave a ball of hot gas or plasma—a star, say—into the black hole. Before it is swallowed, it has a very high entropy, but as soon as it is accreted, you have only empty space and the black hole with entropy zero. You've just lowered the entropy of the universe, and the Second Law of Thermodynamics says that cannot ever happen. Some may argue that the Second Law is “transcended” in a circumstance like this, but it is a pill which few physicists are willing to swallow, especially since in this case it occurs in a completely classical context on a large scale where statistical mechanics obtains. It was this puzzle which led Jacob Bekenstein to propose that black holes did, in fact, have an entropy which was proportional to the area of the event horizon in units of Planck length squared. Black holes not only have entropy, they have a huge amount of it, and account for the overwhelming majority of entropy in the universe. Stephen Hawking subsequently reasoned that if a black hole has entropy, it must have temperature and radiate, and eventually worked out the mechanism of Hawking radiation and the evaporation of black holes.

But if a black hole can evaporate, what happens to the information (more precisely, the quantum state) of the material which collapsed into the black hole in the first place? Hawking argued that it was lost: the evaporation of the black hole was a purely thermal process which released none of the information lost down the black hole. But one of the foundations of quantum mechanics is that information is never lost; it may be scrambled in complex scattering processes to such an extent that you can't reconstruct the initial state, but in principle if you had complete knowledge of the state vector you could evolve the system backward and arrive at the initial configuration. If a black hole permanently destroys information, this wrecks the predictability of quantum mechanics and with it all of microscopic physics.

This book chronicles the author's quest to find out what happens to information that falls into a black hole and discover the mechanism by which information swallowed by the black hole is eventually restored to the universe when the black hole evaporates. The reader encounters string theory, the holographic principle, D-branes, anti de Sitter space, and other arcana, and is eventually led to the explanation that a black hole is really just an enormous ball of string, which encodes in its structure and excitations all of the information of the individual fundamental strings swallowed by the hole. As the black hole evaporates, little bits of this string slip outside the event horizon and zip away as fundamental particles, carrying away the information swallowed by the hole.

The story is told largely through analogies and is easy to follow if you accept the author's premises. I found the tone of the book quite difficult to take, however. The word which kept popping into my head as I made my way through was “smug”. The author opines on everything and anything, and comes across as scornful of anybody who disagrees with his opinions. He is bemused and astonished when he discovers that somebody who is a Republican, an evangelical Christian, or some other belief at variance with the dogma of the academic milieu he inhabits can, nonetheless, actually be a competent scientist. He goes on for two pages (pp. 280–281) making fun of Mormonism and then likens Stephen Hawking to a cult leader. The physics is difficult enough to explain; who cares about what Susskind thinks about everything else? Sometimes he goes right over the top, resulting in unseemly prose like the following.

Although the Black Hole War should have come to an end in early 1998, Stephen Hawking was like one of those unfortunate soldiers who wander in the jungle for years, not knowing that the hostilities have ended. By this time, he had become a tragic figure. Fifty-six years old, no longer at the height of his intellectual powers, and almost unable to communicate, Stephen didn't get the point. I am certain that it was not because of his intellectual limitations. From the interactions I had with him well after 1998, it was obvious that his mind was still extremely sharp. But his physical abilities had so badly deteriorated that he was almost completely locked within his own head. With no way to write an equation and tremendous obstacles to collaborating with others, he must have found it impossible to do the things physicists ordinarily do to understand new, unfamiliar work. So Stephen went on fighting for some time. (p. 419)

Or, Prof. Susskind, perhaps it's that the intellect of Prof. Hawking makes him sceptical of arguments based a “theory” which is, as you state yourself on p. 384, “like a very complicated Tinkertoy set, with lots of different parts that can fit together in consistent patterns”; for which not a single fundamental equation has yet been written down; in which no model that remotely describes the world in which we live has been found; whose mathematical consistency and finiteness in other than toy models remains conjectural; whose results regarding black holes are based upon another conjecture (AdS/CFT) which, even if proven, operates in a spacetime utterly unlike the one we inhabit; which seems to predict a vast “landscape” of possible solutions (vacua) which make it not a theory of everything but rather a “theory of anything”; which is formulated in a flat Minkowski spacetime, neglecting the background independence of general relativity; and which, after three decades of intensive research by some of the most brilliant thinkers in theoretical physics, has yet to make a single experimentally-testable prediction, while demonstrating its ability to wiggle out of almost any result (for example, failure of the Large Hadron Collider to find supersymmetric particles).

At the risk of attracting the scorn the author vents on pp. 186–187 toward non-specialist correspondents, let me say that the author's argument for “black hole complementarity” makes absolutely no sense whatsoever to this layman. In essence, he argues that matter infalling across the event horizon of a black hole, if observed from outside, is disrupted by the “extreme temperature” there, and is excited into its fundamental strings which spread out all over the horizon, preserving the information accreted in the stringy structure of the horizon (whence it can be released as the black hole evaporates). But for a co-moving observer infalling with the matter, nothing whatsoever happens at the horizon (apart from tidal effects whose magnitude depends upon the mass of the black hole). Susskind argues that since you have to choose your frame of reference and cannot simultaneously observe the event from both outside the horizon and falling across it, there is no conflict between these two descriptions, and hence they are complementary in the sense Bohr described quantum observables.

But, unless I'm missing something fundamental, the whole thing about the “extreme temperature” at the black hole event horizon is simply nonsense. Yes, if you lower a thermometer from a space station at some distance from a black hole down toward the event horizon, it will register a diverging temperature as it approaches the horizon. But this is because it is moving near the speed of light with respect to spacetime falling through the horizon and is seeing the cosmic background radiation blueshifted by a factor which reaches infinity at the horizon. Further, being suspended above the black hole, the thermometer is in a state of constant acceleration (it might as well have a rocket keeping it at a specified distance from the horizon as a tether), and is thus in a Rindler spacetime and will measure black body radiation even in a vacuum due to the Unruh effect. But note that due to the equivalence principle, all of this will happen precisely the same even with no black hole. The same thermometer, subjected to the identical acceleration and velocity with respect to the cosmic background radiation frame, will read precisely the same temperature in empty space, with no black hole at all (and will even observe a horizon due to its hyperbolic motion).

The “lowering the thermometer” is a completely different experiment from observing an object infalling to the horizon. The fact that the suspended thermometer measures a high temperature in no way implies that a free-falling object approaching the horizon will experience such a temperature or be disrupted by it. A co-moving observer with the object will observe nothing as it crosses the horizon, while a distant observer will see the object appear to freeze and wink out as it reaches the horizon and the time dilation and redshift approaches infinity. Nowhere is there this legendary string blowtorch at the horizon spreading out the information in the infalling object around a horizon which, observed from either perspective, is just empty space.

The author concludes, in a final chapter titled “Humility”, “The Black Hole War is over…”. Well, maybe, but for this reader, the present book did not make the sale. The arguments made here are based upon aspects of string theory which are, at the moment, purely conjectural and models which operate in universes completely different from the one we inhabit. What happens to information that falls into a black hole? Well, Stephen Hawking has now conceded that it is preserved and released in black hole evaporation (but this assumes an anti de Sitter spacetime, which we do not inhabit), but this book just leaves me shaking my head at the arm waving arguments and speculative theorising presented as definitive results.

April 2009 

Tegmark, Max. Our Mathematical Universe. New York: Alfred A. Knopf, 2014. ISBN 978-0-307-59980-3.

In 1960, physicist Eugene Wigner wrote an essay titled “The Unreasonable Effectiveness of Mathematics in the Natural Sciences” in which he observed that “the enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and that there is no rational explanation for it”. Indeed, each time physics has expanded the horizon of its knowledge from the human scale, whether outward to the planets, stars, and galaxies; or inward to molecules, atoms, nucleons, and quarks it has been found that mathematical theories which precisely model these levels of structure can be found, and that these theories almost always predict new phenomena which are subsequently observed when experiments are performed to look for them. And yet it all seems very odd. The universe seems to obey laws written in the language of mathematics, but when we look at the universe we don't see anything which itself looks like mathematics. The mystery then, as posed by Stephen Hawking, is “What is it that breathes fire into the equations and makes a universe for them to describe?”

This book describes the author's personal journey to answer these deep questions. Max Tegmark, born in Stockholm, is a professor of physics at MIT who, by his own description, leads a double life. He has been a pioneer in developing techniques to tease out data about the early structure of the universe from maps of the cosmic background radiation obtained by satellite and balloon experiments and, in doing so, has been an important contributor to the emergence of precision cosmology: providing precise information on the age of the universe, its composition, and the seeding of large scale structure. This he calls his Dr. Jekyll work, and it is described in detail in the first part of the book. In the balance, his Mr. Hyde persona asserts itself and he delves deeply into the ultimate structure of reality.

He argues that just as science has in the past shown our universe to be far larger and more complicated than previously imagined, our contemporary theories suggest that everything we observe is part of an enormously greater four-level hierarchy of multiverses, arranged as follows.

The level I multiverse consists of all the regions of space outside our cosmic horizon from which light has not yet had time to reach us. If, as precision cosmology suggests, the universe is, if not infinite, so close as to be enormously larger than what we can observe, there will be a multitude of volumes of space as large as the one we can observe in which the laws of physics will be identical but the randomly specified initial conditions will vary. Because there is a finite number of possible quantum states within each observable radius and the number of such regions is likely to be much larger, there will be a multitude of observers just like you, and even more which will differ in various ways. This sounds completely crazy, but it is a straightforward prediction from our understanding of the Big Bang and the measurements of precision cosmology.

The level II multiverse follows directly from the theory of eternal inflation, which explains many otherwise mysterious aspects of the universe, such as why its curvature is so close to flat, why the cosmic background radiation has such a uniform temperature over the entire sky, and why the constants of physics appear to be exquisitely fine-tuned to permit the development of complex structures including life. Eternal (or chaotic) inflation argues that our level I multiverse (of which everything we can observe is a tiny bit) is a single “bubble” which nucleated when a pre-existing “false vacuum” phase decayed to a lower energy state. It is this decay which ultimately set off the enormous expansion after the Big Bang and provided the energy to create all of the content of the universe. But eternal inflation seems to require that there be an infinite series of bubbles created, all causally disconnected from one another. Because the process which causes a bubble to begin to inflate is affected by quantum fluctuations, although the fundamental physical laws in all of the bubbles will be the same, the initial conditions, including physical constants, will vary from bubble to bubble. Some bubbles will almost immediately recollapse into a black hole, others will expand so rapidly stars and galaxies never form, and in still others primordial nucleosynthesis may result in a universe filled only with helium. We find ourselves in a bubble which is hospitable to our form of life because we can only exist in such a bubble.

The level III multiverse is implied by the unitary evolution of the wave function in quantum mechanics and the multiple worlds interpretation which replaces collapse of the wave function with continually splitting universes in which every possible outcome occurs. In this view of quantum mechanics there is no randomness—the evolution of the wave function is completely deterministic. The results of our experiments appear to contain randomness because in the level III multiverse there are copies of each of us which experience every possible outcome of the experiment and we don't know which copy we are. In the author's words, “…causal physics will produce the illusion of randomness from your subjective viewpoint in any circumstance where you're being cloned. … So how does it feel when you get cloned? It feels random! And every time something fundamentally random appears to happen to you, which couldn't have been predicted even in principle, it's a sign that you've been cloned.”

In the level IV multiverse, not only do the initial conditions, physical constants, and the results of measuring an evolving quantum wave function vary, but the fundamental equations—the mathematical structure—of physics differ. There might be a different number of spatial dimensions, or two or more time dimensions, for example. The author argues that the ultimate ensemble theory is to assume that every mathematical structure exists as a physical structure in the level IV multiverse (perhaps with some constraints: for example, only computable structures may have physical representations). Most of these structures would not permit the existence of observers like ourselves, but once again we shouldn't be surprised to find ourselves living in a structure which allows us to exist. Thus, finally, the reason mathematics is so unreasonably effective in describing the laws of physics is just that mathematics and the laws of physics are one and the same thing. Any observer, regardless of how bizarre the universe it inhabits, will discover mathematical laws underlying the phenomena within that universe and conclude they make perfect sense.

Tegmark contends that when we try to discover the mathematical structure of the laws of physics, the outcome of quantum measurements, the physical constants which appear to be free parameters in our models, or the detailed properties of the visible part of our universe, we are simply trying to find our address in the respective levels of these multiverses. We will never find a reason from first principles for these things we measure: we observe what we do because that's the way they are where we happen to find ourselves. Observers elsewhere will see other things.

The principal opposition to multiverse arguments is that they are unscientific because they posit phenomena which are unobservable, perhaps even in principle, and hence cannot be falsified by experiment. Tegmark takes a different tack. He says that if you have a theory (for example, eternal inflation) which explains observations which otherwise do not make any sense and has made falsifiable predictions (the fine-scale structure of the cosmic background radiation) which have subsequently been confirmed by experiment, then if it predicts other inevitable consequences (the existence of a multitude of other Hubble volume universes outside our horizon and other bubbles with different physical constants) we should take these predictions seriously, even if we cannot think of any way at present to confirm them. Consider gravitational radiation: Einstein predicted it in 1916 as a consequence of general relativity. While general relativity has passed every experimental test in subsequent years, at the time of Einstein's prediction almost nobody thought a gravitational wave could be detected, and yet the consistency of the theory, validated by other tests, persuaded almost all physicists that gravitational waves must exist. It was not until the 1980s that indirect evidence for this phenomenon was detected, and to this date, despite the construction of elaborate apparatus and the efforts of hundreds of researchers over decades, no direct detection of gravitational radiation has been achieved.

There is a great deal more in this enlightening book. You will learn about the academic politics of doing highly speculative research, gaming the arXiv to get your paper listed as the first in the day's publications, the nature of consciousness and perception and its complex relation to consensus and external reality, the measure problem as an unappreciated deep mystery of cosmology, whether humans are alone in our observable universe, the continuum versus an underlying discrete structure, and the ultimate fate of our observable part of the multiverses.

In the Kindle edition, everything is properly linked, including the comprehensive index. Citations of documents on the Web are live links which may be clicked to display them.

March 2014 

Thorne, Kip. The Science of Interstellar. New York: W. W. Norton, 2014. ISBN 978-0-393-35137-8.

Christopher Nolan's 2014 film Interstellar was eagerly awaited by science fiction enthusiasts who, having been sorely disappointed so many times by movies that crossed the line into fantasy by making up entirely implausible things to move the plot along, hoped that this effort would live up to its promise of getting the science (mostly) right and employing scientifically plausible speculation where our present knowledge is incomplete.

The author of the present book is one of the most eminent physicists working in the field of general relativity (Einstein's theory of gravitation) and a pioneer in exploring the exotic strong field regime of the theory, including black holes, wormholes, and gravitational radiation. Prof. Thorne was involved in the project which became Interstellar from its inception, and worked closely with the screenwriters, director, and visual effects team to get the science right. Some of the scenes in the movie, such as the visual appearance of orbiting a rotating black hole, have never been rendered accurately before, and are based upon original work by Thorne in computing light paths through spacetime in its vicinity which will be published as professional papers.

Here, the author recounts the often bumpy story of the movie's genesis and progress over the years from his own, Hollywood-outsider, perspective, how the development of the story presented him, as technical advisor (he is credited as an executive producer), with problem after problem in finding a physically plausible solution, sometimes requiring him to do new physics. Then, Thorne provides a popular account of the exotic physics on which the story is based, including gravitational time dilation, black holes, wormholes, and speculative extra dimensions and “brane” scenarios stemming from string theory. Then he “interprets” the events and visual images in the film, explaining (where possible) how they could be produced by known, plausible, or speculative physics. Of course, this isn't always possible—in some cases the needs of story-telling or the requirement not to completely baffle a non-specialist with bewilderingly complicated and obscure images had to take priority over scientific authenticity, and when this is the case Thorne is forthright in admitting so.

Sections are labelled with icons identifying them as “truth”: generally accepted by those working in the field and often with experimental evidence, “educated guess”: a plausible inference from accepted physics, but without experimental evidence and assuming existing laws of physics remain valid in circumstances under which we've never tested them, and “speculation”: wild and wooly stuff (for example quantum gravity or the interior structure of a black hole) which violates no known law of physics, but for which we have no complete and consistent theory and no evidence whatsoever.

This is a clearly written and gorgeously illustrated book which, for those who enjoyed the movie but weren't entirely clear whence some of the stunning images they saw came, will explain the science behind them. The cover of the book has a “SPOILER ALERT” warning potential readers that the ending and major plot details are given away in the text. I will refrain from discussing them here so as not to make this a spoiler in itself. I have not yet seen the movie, and I expect when I do I will enjoy it more for having read the book, since I'll know what to look for in some of the visuals and be less likely to dismiss some of the apparently outrageous occurrences by knowing that there is a physically plausible (albeit extremely speculative and improbable) explanation for them.

For the animations and blackboard images mentioned in the text, the book directs you to a Web site which is so poorly designed and difficult to navigate it took me ten minutes to find them on the first visit. Here is a direct link. In the Kindle edition the index cites page numbers in the print edition which are useless since the electronic edition does not contain real page numbers. There are a few typographical errors and one factual howler: Io is not “Saturn's closest moon”, and Cassini was captured in Saturn orbit by a propulsion burn, not a gravitational slingshot (this does not affect the movie in any way: it's in background material).

December 2014 

Tipler, Frank J. The Physics of Christianity. New York: Doubleday, 2007. ISBN 0-385-51424-7.

Oh. My. Goodness. Are you yearning for answers to the Big Questions which philosophers and theologians have puzzled over for centuries? Here you are, using direct quotes from this book in the form of a catechism of this beyond-the-fringe science cataclysm.

What is the purpose of life in the universe?

It is not enough to annihilate some baryons. If the laws of physics are to be consistent over all time, a substantial percentage of all the baryons in the universe must be annihilated, and over a rather short time span. Only if this is done will the acceleration of the universe be halted. This means, in particular, that intelligent life from the terrestrial biosphere must move out into interstellar and intergalactic space, annihilating baryons as they go. (p. 67)

What is the nature of God?

God is the Cosmological Singularity. A singularity is an entity that is outside of time and space—transcendent to space and time—and it is the only thing that exists that is not subject to the laws of physics. (p. 269)

How can the three persons of the Trinity be one God?

The Cosmological Singularity consists of three Hypostases: the Final Singularity, the All-Presents Singularity, and the Initial Singularity. These can be distinguished by using Cauchy sequences of different sorts of person, so in the Cauchy completion, they become three distinct Persons. But still, the three Hypostases of the Singularity are just one Singularity. The Trinity, in other words, consists of three Persons but only one God. (pp. 269–270.)

How did Jesus walk on water?

For example, walking on water could be accomplished by directing a neutrino beam created just below Jesus' feet downward. If we ourselves knew how to do this, we would have the perfect rocket! (p. 200)

What is Original Sin?

If Original Sin actually exists, then it must in some way be coded in our genetic material, that is, in our DNA. … By the time of the Cambrian Explosion, if not earlier, carnivores had appeared on Earth. Evil had appeared in the world. Genes now coded for behavior that guided the use of biological weapons of the carnivores. The desire to do evil was now hereditary. (pp. 188, 190)

How can long-dead saints intercede in the lives of people who pray to them?

According to the Universal Resurrection theory, everyone, in particular the long-dead saints, will be brought back into existence as computer emulations in the far future, near the Final Singularity, also called God the Father. … Future-to-past causation is usual with the Cosmological Singularity. A prayer made today can be transferred by the Singularity to a resurrected saint—the Virgin Mary, say—after the Universal Resurrection. The saint can then reflect on the prayer and, by means of the Son Singularity acting through the multiverse, reply. The reply, via future-to-past causation, is heard before it is made. It is heard billions of years before it is made. (p. 235)

When will the End of Days come?

In summary, by the year 2050 at the latest, we will see:

1. Intelligent machines more intelligent than humans.
2. Human downloads, effectively invulnerable and far more capable than normal humans.
3. Most of humanity Christian.
4. Effectively unlimited energy
5. A rocket capable of interstellar travel.
6. Bombs that are to atomic bombs as atomic bombs are to spitballs, and these weapons will be possessed by practically anybody who wants one.

(p. 253)

Hey, I said answers, not correct answers! This is only a tiny sampler of the side-splitting “explanations” of Christian mysteries and miracles in this book. Others include the virgin birth, the problem of evil, free will, the resurrection of Jesus, the shroud of Turin and the holy grail, the star of Bethlehem, transubstantiation, quantum gravity, the second coming, and more, more, more. Quoting them all would mean quoting almost the whole book—if you wish to be awed by or guffaw at them all, you're going to have to read the whole thing. And that's not all, since it seems like every other page or so there's a citation of Tipler's 1994 opus, The Physics of Immortality (read my review), so some sections are likely to be baffling unless you suspend disbelief and slog your way through that tome as well.

Basically, Tipler sees your retro-causality and raises to retro-teleology. In order for the laws of physics, in particular the unitarity of quantum mechanics, to be valid, then the universe must evolve to a final singularity with no event horizons—the Omega Point. But for this to happen, as it must, since the laws of physics are never violated, then intelligent life must halt the accelerating expansion of the universe and turn it around into contraction. Because this must happen, the all-knowing Final Singularity, which Tipler identifies with God the Father, acts as a boundary condition which causes fantastically improbable events such as the simultaneous tunnelling disintegration of every atom of the body of Jesus into neutrinos to become certainties, because otherwise the Final Singularity Omega Point will not be formed. Got that?

I could go on and on, but by now I think you'll have gotten the point, even if it isn't an Omega Point. The funny thing is, I'm actually sympathetic to much of what Tipler says here: his discussion of free will in the multiverse and the power of prayer or affirmation is not that unlike what I suggest in my eternally under construction “General Theory of Paranormal Phenomena”, and I share Tipler's optimism about the human destiny and the prospects, in a universe of which 95% of the mass is made of stuff we know absolutely nothing about, of finding sources of energy as boundless and unimagined as nuclear fission and fusion were a century ago. But folks, this is just silly. One of the most irritating things is Tipler's interpreting scripture to imply a deep knowledge of recently-discovered laws of physics and then turning around, a few pages later, when the argument requires it, to claim that another passage was influenced by contemporary beliefs of the author which have since been disproved. Well, which is it?

If you want to get a taste of this material, see “The Omega Point and Christianity”, which contains much of the physics content of the book in preliminary form. The entire first chapter of the published book can be downloaded in icky Microsoft Word format from the author's Web site, where additional technical and popular articles are available.

For those unacquainted with the author, Frank J. Tipler is a full professor of mathematical physics at Tulane University in New Orleans, pioneer in global methods in general relativity, discoverer of the massive rotating cylinder time machine, one of the first to argue that the resolution of the Fermi Paradox is, as his paper was titled, “Extraterrestrial Intelligent Beings Do Not Exist”, and, with John Barrow, author of The Anthropic Cosmological Principle, the definitive work on that topic. Say what you like, but Tipler is a serious and dedicated scientist with world-class credentials who believes that the experimentally-tested laws of physics as we understand them are not only consistent with, but require, many of the credal tenets which traditional Christians have taken on faith. The research program he proposes (p. 271), “… would make Christianity a branch of physics.” Still, as I wrote almost twelve years ago, were I he, I'd be worried about getting on the wrong side of the Old One.

Finally, and this really bothers me, I can't close these remarks without mentioning that notwithstanding there being an entire chapter titled “Anti-Semitism Is Anti-Christian” (pp. 243–256), which purports to explain it on the last page, this book is dedicated, “To God's Chosen People, the Jews, who for the first time in 2,000 years are advancing Christianity.” I've read the book; I've read the explanation; and this remark still seems both puzzling and disturbing to me.

June 2007 

Unger, Roberto Mangabeira and Lee Smolin. The Singular Universe and the Reality of Time. Cambridge: Cambridge University Press, 2015. ISBN 978-1-107-07406-4.

In his 2013 book Time Reborn (June 2013), Lee Smolin argued that, despite its extraordinary effectiveness in understanding the behaviour of isolated systems, what he calls the “Newtonian paradigm” is inadequate to discuss cosmology: the history and evolution of the universe as a whole. In this book, Smolin and philosopher Roberto Mangabeira Unger expand upon that observation and present the case that the current crisis in cosmology, with its appeal to multiple universes and mathematical structures which are unobservable, even in principle, is a consequence of the philosophical, scientific, and mathematical tools we've been employing since the dawn of science attempting to be used outside their domain of applicability, and that we must think differently when speaking of the universe as a whole, which contains all of its own causes and obeys no laws outside itself. The authors do not present their own theories to replace those of present-day cosmology (although they discuss the merits of several proposals), but rather describe their work as a “proposal in natural philosophy” which might guide investigators searching for those new theories.

In brief, the Newtonian paradigm is that the evolution of physical systems is described by differential equations which, given a set of initial conditions, permit calculating the evolution of a system in the future. Since the laws of physics at the microscopic level are reversible, given complete knowledge of the state of a system at a given time, its past can equally be determined. Quantum mechanics modifies this only in that rather than calculating the position and momentum of particles (or other observables), we calculate the deterministic evolution of the wave function which gives the probability of observing them in specific states in the future.

This paradigm divides physics into two components: laws (differential equations) and initial conditions (specification of the initial state of the system being observed). The laws themselves, although they allow calculating the evolution of the system in time, are themselves timeless: they do not change and are unaffected by the interaction of objects. But if the laws are timeless and not subject to back-reaction by the objects whose interaction they govern, where did they come from and where do they exist? While conceding that these aren't matters which working scientists spend much time thinking about, in the context of cosmology they post serious philosophical problems. If the universe all that is and contains all of its own causes, there is no place for laws which are outside the universe, cannot be acted upon by objects within it, and have no apparent cause.

Further, because mathematics has been so effective in expressing the laws of physics we've deduced from experiments and observations, many scientists have come to believe that mathematics can be a guide to exploring physics and cosmology: that some mathematical objects we have explored are, in a sense, homologous to the universe, and that learning more about the mathematics can be a guide to discoveries about reality.

One of the most fundamental discoveries in cosmology, which has happened within the lifetimes of many readers of this book, including me, is that the universe has a history. When I was a child, some scientists (a majority, as I recall) believed the universe was infinite and eternal, and that observers at any time in the past or future would observe, at the largest scales, pretty much the same thing. Others argued for an origin at a finite time in the past, with the early universe having a temperature and density much greater than at present—this theory was mocked as the “big bang”. Discovery of the cosmic background radiation and objects in the distant universe which did not at all resemble those we see nearby decisively decided this dispute in favour of the big bang, and recent precision measurements have allowed determination of when it happened and how the universe evolved subsequently.

If the universe has a finite age, this makes the idea of timeless laws even more difficult to accept. If the universe is eternal, one can accept that the laws we observe have always been that way and always will be. But if the universe had an origin we can observe, how did the laws get baked into the universe? What happened before the origin we observe? If every event has a cause, what was the cause of the big bang?

The authors argue that in cosmology—a theory encompassing the entire universe—a global privileged time must govern all events. Time flows not from some absolute clock as envisioned by Newtonian physics or the elastic time of special and general relativity, but from causality: every event has one or more causes, and these causes are unique. Depending upon their position and state of motion, observers will disagree about the durations measured by their own clocks, and on the order in which things at different positions in space occurred (the relativity of simultaneity), but they will always observe a given event to have the same cause(s), which precede it. This relational notion of time, they argue, is primordial, and space may be emergent from it.

Given this absolute and privileged notion of time (which many physicists would dispute, although the authors argue does not conflict with relativity), that time is defined by the causality of events which cause change in the universe, and that there is a single universe with nothing outside it and which contains all of its own causes, then is it not plausible to conclude that the “laws” of physics which we observe are not timeless laws somehow outside the universe or grounded in a Platonic mathematics beyond the universe, but rather have their own causes, within the universe, and are subject to change: just as there is no “unmoved mover”, there is no timeless law? The authors, particularly Smolin, suggest that just as we infer laws from observing regularities in the behaviour of systems within the universe when performing experiments in various circumstances, these laws emerge as the universe develops “habits” as interactions happen over and over. In the present cooled-down state of the universe, it's very much set in its ways, and since everything has happened innumerable times we observe the laws to be unchanging. But closer to the big bang or at extreme events in the subsequent universe, those habits haven't been established and true novelty can occur. (Indeed, simply by synthesising a protein with a hundred amino acids at random, you're almost certain to have created a molecule which has never existed before in the observable universe, and it may be harder to crystallise the first time than subsequently. This appears to be the case. This is my observation, not the authors'.)

Further, not only may the laws change, but entirely new kinds of change may occur: change itself can change. For example, on Earth, change was initially governed entirely by the laws of physics and chemistry (with chemistry ultimately based upon physics). But with the emergence of life, change began to be driven by evolution which, while at the molecular level was ultimately based upon chemistry, created structures which equilibrium chemistry never could, and dramatically changed the physical environment of the planet. This was not just change, but a novel kind of change. If it happened here, in our own recent (in cosmological time) history, why should we assume other novel kinds of change did not emerge in the early universe, or will not continue to manifest themselves in the future?

This is a very difficult and somewhat odd book. It is written in two parts, each by one of the co-authors, largely independent of one another. There is a twenty page appendix in which the authors discuss their disagreements with one another, some of which are fundamental. I found Unger's part tedious, repetitive, and embodying all of things I dislike about academic philosophers. He has some important things to say, but I found that slogging through almost 350 pages of it was like watching somebody beat a moose to death with an aluminium baseball bat: I believe a good editor, or even a mediocre one, could have cut this to 50 pages without losing anything and making the argument more clearly than trying to dig it out of this blizzard of words. Lee Smolin is one of the most lucid communicators among present-day research scientists, and his part is clear, well-argued, and a delight to read; it's just that you have to slog through the swamp to get there.

While suggesting we may have been thinking about cosmology all wrong, this is not a book which suggests either an immediate theoretical or experimental programme to explore these new ideas. Instead, it intends to plant the seed that, apart from time and causality, everything may be emergent, and that when we think about the early universe we cannot rely upon the fixed framework of our cooled-down universe with its regularities. Some of this is obvious and non-controversial: before there were atoms, there was no periodic table of the elements. But was there a time before there was conservation of energy, or before locality?

September 2015 

van Dongen, Jeroen. Einstein's Unification. Cambridge: Cambridge University Press, 2010. ISBN 978-0-521-88346-7.

In 1905 Albert Einstein published four papers which transformed the understanding of space, time, mass, and energy; provided physical evidence for the quantisation of energy; and observational confirmation of the existence of atoms. These publications are collectively called the Annus Mirabilis papers, and vaulted the largely unknown Einstein to the top rank of theoretical physicists. When Einstein was awarded the Nobel Prize in Physics in 1921, it was for one of these 1905 papers which explained the photoelectric effect. Einstein's 1905 papers are masterpieces of intuitive reasoning and clear exposition, and demonstrated Einstein's technique of constructing thought experiments based upon physical observations, then deriving testable mathematical models from them. Unlike so many present-day scientific publications, Einstein's papers on special relativity and the equivalence of mass and energy were accessible to anybody with a college-level understanding of mechanics and electrodynamics and used no special jargon or advanced mathematics. Being based on well-understood concepts, neither cited any other scientific paper.

While special relativity revolutionised our understanding of space and time, and has withstood every experimental test to which it has been subjected in the more than a century since it was formulated, it was known from inception that the theory was incomplete. It's called special relativity because it only describes the behaviour of bodies under the special case of uniform unaccelerated motion in the absence of gravity. To handle acceleration and gravitation would require extending the special theory into a general theory of relativity, and it is upon this quest that Einstein next embarked.

As before, Einstein began with a simple thought experiment. Just as in special relativity, where there is no experiment which can be done in a laboratory without the ability to observe the outside world that can determine its speed or direction of uniform (unaccelerated) motion, Einstein argued that there should be no experiment an observer could perform in a sufficiently small closed laboratory which could distinguish uniform acceleration from the effect of gravity. If one observed objects to fall with an acceleration equal to that on the surface of the Earth, the laboratory might be stationary on the Earth or in a space ship accelerating with a constant acceleration of one gravity, and no experiment could distinguish the two situations. (The reason for the “sufficiently small” qualification is that since gravity is produced by massive objects, the direction a test particle will fall depends upon its position with respect to the centre of gravity of the body. In a very large laboratory, objects dropped far apart would fall in different directions. This is what causes tides.)

Einstein called this observation the “equivalence principle”: that the effects of acceleration and gravity are indistinguishable, and that hence a theory which extended special relativity to incorporate accelerated motion would necessarily also be a theory of gravity. Einstein had originally hoped it would be straightforward to reconcile special relativity with acceleration and gravity, but the deeper he got into the problem, the more he appreciated how difficult a task he had undertaken. Thanks to the Einstein Papers Project, which is curating and publishing all of Einstein's extant work, including notebooks, letters, and other documents, the author (a participant in the project) has been able to reconstruct Einstein's ten-year search for a viable theory of general relativity.

Einstein pursued a two-track approach. The bottom up path started with Newtonian gravity and attempted to generalise it to make it compatible with special relativity. In this attempt, Einstein was guided by the correspondence principle, which requires that any new theory which explains behaviour under previously untested conditions must reproduce the tested results of existing theory under known conditions. For example, the equations of motion in special relativity reduce to those of Newtonian mechanics when velocities are small compared to the speed of light. Similarly, for gravity, any candidate theory must yield results identical to Newtonian gravitation when field strength is weak and velocities are low.

From the top down, Einstein concluded that any theory compatible with the principle of equivalence between acceleration and gravity must exhibit general covariance, which can be thought of as being equally valid regardless of the choice of co-ordinates (as long as they are varied without discontinuities). There are very few mathematical structures which have this property, and Einstein was drawn to Riemann's tensor geometry. Over years of work, Einstein pursued both paths, producing a bottom-up theory which was not generally covariant which he eventually rejected as in conflict with experiment. By November 1915 he had returned to the top-down mathematical approach and in four papers expounded a generally covariant theory which agreed with experiment. General relativity had arrived.

Einstein's 1915 theory correctly predicted the anomalous perihelion precession of Mercury and also predicted that starlight passing near the limb of the Sun would be deflected by twice the angle expected based on Newtonian gravitation. This was confirmed (within a rather large margin of error) in an eclipse expedition in 1919, which made Einstein's general relativity front page news around the world. Since then precision tests of general relativity have tested a variety of predictions of the theory with ever-increasing precision, with no experiment to date yielding results inconsistent with the theory.

Thus, by 1915, Einstein had produced theories of mechanics, electrodynamics, the equivalence of mass and energy, and the mechanics of bodies under acceleration and the influence of gravitational fields, and changed space and time from a fixed background in which physics occurs to a dynamical arena: “Matter and energy tell spacetime how to curve. Spacetime tells matter how to move.” What do you do, at age 36, having figured out, largely on your own, how a large part of the universe works?

Much of Einstein's work so far had consisted of unification. Special relativity unified space and time, matter and energy. General relativity unified acceleration and gravitation, gravitation and geometry. But much remained to be unified. In general relativity and classical electrodynamics there were two field theories, both defined on the continuum, both with unlimited range and an inverse square law, both exhibiting static and dynamic effects (although the details of gravitomagnetism would not be worked out until later). And yet the theories seemed entirely distinct: gravity was always attractive and worked by the bending of spacetime by matter-energy, while electromagnetism could be either attractive or repulsive, and seemed to be propagated by fields emitted by point charges—how messy.

Further, quantum theory, which Einstein's 1905 paper on the photoelectric effect had helped launch, seemed to point in a very different direction than the classical field theories in which Einstein had worked. Quantum mechanics, especially as elaborated in the “new” quantum theory of the 1920s, seemed to indicate that aspects of the universe such as electric charge were discrete, not continuous, and that physics could, even in principle, only predict the probability of the outcome of experiments, not calculate them definitively from known initial conditions. Einstein never disputed the successes of quantum theory in explaining experimental results, but suspected it was a theory based upon phenomena which did not explain what was going on at a deeper level. (For example, the physical theory of elasticity explains experimental results and makes predictions within its domain of applicability, but it is not fundamental. All of the effects of elasticity are ultimately due to electromagnetic forces between atoms in materials. But that doesn't mean that the theory of elasticity isn't useful to engineers, or that they should do their spring calculations at the molecular level.)

Einstein undertook the search for a unified field theory, which would unify gravity and electromagnetism, just as Maxwell had unified electrostatics and magnetism into a single theory. In addition, Einstein believed that a unified field theory would be antecedent to quantum theory, and that the probabilistic results of quantum theory could be deduced from the more fundamental theory, which would remain entirely deterministic. From 1915 until his death in 1955 Einstein's work concentrated mostly on the quest for a unified field theory. He was aided by numerous talented assistants, many of whom went on to do important work in their own right. He explored a variety of paths to such a theory, but ultimately rejected each one, in turn, as either inconsistent with experiment or unable to explain phenomena such as point particles or quantisation of charge.

As the author documents, Einstein's approach to doing physics changed in the years after 1915. While before he was guided both by physics and mathematics, in retrospect he recalled and described his search of the field equations of general relativity as having followed the path of discovering the simplest and most elegant mathematical structure which could explain the observed phenomena. He thus came, like Dirac, to argue that mathematical beauty was the best guide to correct physical theories.

In the last forty years of his life, Einstein made no progress whatsoever toward a unified field theory, apart from discarding numerous paths which did not work. He explored a variety of approaches: “semivectors” (which turned out just to be a reformulation of spinors), five-dimensional models including a cylindrically compactified dimension based on Kaluza-Klein theory, and attempts to deduce the properties of particles and their quantum behaviour from nonlinear continuum field theories.

In seeking to unify electromagnetism and gravity, he ignored the strong and weak nuclear forces which had been discovered over the years and merited being included in any grand scheme of unification. In the years after World War II, many physicists ceased to worry about the meaning of quantum mechanics and the seemingly inherent randomness in its predictions which so distressed Einstein, and adopted a “shut up and calculate” approach as their computations were confirmed to ever greater precision by experiments.

So great was the respect for Einstein's achievements that only rarely was a disparaging word said about his work on unified field theories, but toward the end of his life it was outside the mainstream of theoretical physics, which had moved on to elaboration of quantum theory and making quantum theory compatible with special relativity. It would be a decade after Einstein's death before astronomical discoveries would make general relativity once again a frontier in physics.

What can we learn from the latter half of Einstein's life and his pursuit of unification? The frontier of physics today remains unification among the forces and particles we have discovered. Now we have three forces to unify (counting electromagnetism and the weak nuclear force as already unified in the electroweak force), plus two seemingly incompatible kinds of particles: bosons (carriers of force) and fermions (what stuff is made of). Six decades (to the day) after the death of Einstein, unification of gravity and the other forces remains as elusive as when he first attempted it.

It is a noble task to try to unify disparate facts and theories into a common whole. Much of our progress in the age of science has come from such unification. Einstein unified space and time; matter and energy; acceleration and gravity; geometry and motion. We all benefit every day from technologies dependent upon these fundamental discoveries. He spent the last forty years of his life seeking the next grand unification. He never found it. For this effort we should applaud him.

I must remark upon how absurd the price of this book is. At Amazon as of this writing, the hardcover is US$ 102.91 and the Kindle edition is US$ 88. Eighty-eight Yankee dollars for a 224 page book which is ranked #739,058 in the Kindle store?

April 2015 

Vilenkin, Alexander. Many Worlds in One. New York: Hill and Wang, 2006. ISBN 0-8090-9523-8.

From the dawn of the human species until a time within the memory of many people younger than I, the origin of the universe was the subject of myth and a topic, if discussed at all within the academy, among doctors of divinity, not professors of physics. The advent of precision cosmology has changed that: the ultimate questions of origin are not only legitimate areas of research, but something probed by satellites in space, balloons circling the South Pole, and mega-projects of Big Science. The results of these experiments have, in the last few decades, converged upon a consensus from which few professional cosmologists would dissent:

1. At the largest scale, the geometry of the universe is indistinguishable from Euclidean (flat), and the distribution of matter and energy within it is homogeneous and isotropic.
2. The universe evolved from an extremely hot, dense, phase starting about 13.7 billion years ago from our point of observation, which resulted in the abundances of light elements observed today.
3. The evidence of this event is imprinted on the cosmic background radiation which can presently be observed in the microwave frequency band. All large-scale structures in the universe grew from gravitational amplification of scale-independent quantum fluctuations in density.
4. The flatness, homogeneity, and isotropy of the universe is best explained by a period of inflation shortly after the origin of the universe, which expanded a tiny region of space, smaller than a subatomic particle, to a volume much greater than the presently observable universe.
5. Consequently, the universe we can observe today is bounded by a horizon, about forty billion light years away in every direction (greater than the 13.7 billion light years you might expect since the universe has been expanding since its origin), but the universe is much, much larger than what we can see; every year another light year comes into view in every direction.

Now, this may seem mind-boggling enough, but from these premises, which it must be understood are accepted by most experts who study the origin of the universe, one can deduce some disturbing consequences which seem to be logically unavoidable.

Let me walk you through it here. We assume the universe is infinite and unbounded, which is the best estimate from precision cosmology. Then, within that universe, there will be an infinite number of observable regions, which we'll call O-regions, each defined by the volume from which an observer at the centre can have received light since the origin of the universe. Now, each O-region has a finite volume, and quantum mechanics tells us that within a finite volume there are a finite number of possible quantum states. This number, although huge (on the order of 10¹⁰¹²³ for a region the size of the one we presently inhabit), is not infinite, so consequently, with an infinite number of O-regions, even if quantum mechanics specifies the initial conditions of every O-region completely at random and they evolve randomly with every quantum event thereafter, there are only a finite number of histories they can experience (around 10¹⁰¹⁵⁰). Which means that, at this moment, in this universe (albeit not within our current observational horizon), invoking nothing as fuzzy, weird, or speculative as the multiple world interpretation of quantum mechanics, there are an infinite number of you reading these words scribbled by an infinite number of me. In the vast majority of our shared universes things continue much the same, but from time to time they d1v3r93 r4ndtx#e~—….

Reset . . .
Snap back to universe of origin . . .
Reloading initial vacuum parameters . . .
Restoring simulation . . .
Resuming from checkpoint.

What was that? Nothing, I guess. Still, odd, that blip you feel occasionally. Anyway, here is a completely fascinating book by a physicist and cosmologist who is pioneering the ragged edge of what the hard evidence from the cosmos seems to be telling us about the apparently boundless universe we inhabit. What is remarkable about this model is how generic it is. If you accept the best currently available evidence for the geometry and composition of the universe in the large, and agree with the majority of scientists who study such matters how it came to be that way, then an infinite cosmos filled with observable regions of finite size and consequently limited diversity more or less follows inevitably, however weird it may seem to think of an infinity of yourself experiencing every possible history somewhere. Further, in an infinite universe, there are an infinite number of O-regions which contain every possible history consistent with the laws of quantum mechanics and the symmetries of our spacetime including those in which, as the author noted, perhaps using the phrase for the first time in the august pages of the Physical Review, “Elvis is still alive”.

So generic is the prediction, there's no need to assume the correctness of speculative ideas in physics. The author provides a lukewarm endorsement of string theory and the “anthropic landscape” model, but is clear to distinguish its “multiverse” of distinct vacua with different moduli from our infinite universe with (as far as we know) a single, possibly evolving, vacuum state. But string theory could be completely wrong and the deductions from observational cosmology would still stand. For that matter, they are independent of the “eternal inflation” model the book describes in detail, since they rely only upon observables within the horizon of our single “pocket universe”.

Although the evolution of the universe from shortly after the end of inflation (the moment we call the “big bang”) seems to be well understood, there are still deep mysteries associated with the moment of origin, and the ultimate fate of the universe remains an enigma. These questions are discussed in detail, and the author makes clear how speculative and tentative any discussion of such matters must be given our present state of knowledge. But we are uniquely fortunate to be living in the first time in all of history when these profound questions upon which humans have mused since antiquity have become topics of observational and experimental science, and a number of experiments now underway and expected in the next few years which bear upon them are described.

Curiously, the author consistently uses the word “google” for the number 10¹⁰⁰. The correct name for this quantity, coined in 1938 by nine-year-old Milton Sirotta, is “googol”. Edward Kasner, young Milton's uncle, then defined “googolplex” as 10¹⁰¹⁰⁰. “Google^™” is an Internet search engine created by megalomaniac collectivists bent on monetising, without compensation, content created by others. The text is complemented by a number of delightful cartoons reminiscent of those penned by George Gamow, a physicist the author (and this reader) much admires.

October 2006 

Visser, Matt. Lorentzian Wormholes: From Einstein to Hawking. New York: Springer-Verlag, 1996. ISBN 1-56396-653-0.

June 2002 

Weinberg, Steven. Facing Up. Cambridge, MA: Harvard University Press, 2001. ISBN 0-674-01120-1.

This is a collection of non-technical essays written between 1985 and 2000 by Nobel Prize winning physicist Steven Weinberg. Many discuss the “science wars”—the assault by postmodern academics on the claim that modern science is discovering objective truth (well, duh), but many other topics are explored, including string theory, Zionism, Alan Sokal's hoax at the expense of the unwitting (and witless) editors of Social Text, Thomas Kuhn's views on scientific revolutions, science and religion, and the comparative analysis of utopias. Weinberg applies a few basic principles to most things he discusses—I counted six separate defences of reductionism in modern science, most couched in precisely the same terms. You may find this book more enjoyable a chapter at a time over an extended period rather than in one big cover-to-cover gulp.

January 2005 

Weinberger, Sharon. Imaginary Weapons. New York: Nation Books, 2006. ISBN 1-56025-849-7.

A nuclear isomer is an atomic nucleus which, due to having a greater spin, different shape, or differing alignment of the spin orientation and axis of symmetry, has more internal energy than the ground state nucleus with the same number of protons and neutrons. Nuclear isomers are usually produced in nuclear fusion reactions when the the addition of protons and/or neutrons to a nucleus in a high-energy collision leaves it in an excited state. Hundreds of nuclear isomers are known, but the overwhelming majority decay with gamma ray emission in about 10⁻¹⁴ seconds. In a few species, however, this almost instantaneous decay is suppressed for various reasons, and metastable isomers exist with half-lives ranging from 10⁻⁹ seconds (one nanosecond), to the isomer Tantalum-180m, which has a half-life of at least 10¹⁵ years and may be entirely stable; it is the only nuclear isomer found in nature and accounts for about one atom of 8300 in tantalum metal.

Some metastable isomers with intermediate half-lives have a remarkably large energy compared to the ground state and emit correspondingly energetic gamma ray photons when they decay. The Hafnium-178m2 (the “m2” denotes the second lowest energy isomeric state) nucleus has a half-life of 31 years and decays (through the m1 state) with the emission of 2.45 MeV in gamma rays. Now the fact that there's a lot of energy packed into a radioactive nucleus is nothing new—people were calculating the energy of disintegrating radium and uranium nuclei at the end of the 19th century, but all that energy can't be used for much unless you can figure out some way to release it on demand—as long as it just dribbles out at random, you can use it for some physics experiments and medical applications, but not to make loud bangs or turn turbines. It was only the discovery of the fission chain reaction, where the fission of certain nuclei liberates neutrons which trigger the disintegration of others in an exponential process, which made nuclear energy, for better or for worse, accessible.

So, as long as there is no way to trigger the release of the energy stored in a nuclear isomer, it is nothing more than an odd kind of radioactive element, the subject of a reasonably well-understood and somewhat boring topic in nuclear physics. If, however, there were some way to externally trigger the decay of the isomer to the ground state, then the way would be open to releasing the energy in the isomer at will. It is possible to trigger the decay of the Tantalum-180 isomer by 2.8 MeV photons, but the energy required to trigger the decay is vastly greater than the 0.075 MeV it releases, so the process is simply an extremely complicated and expensive way to waste energy.

Researchers in the small community interested in nuclear isomers were stunned when, in the January 25, 1999 issue of Physical Review Letters, a paper by Carl Collins and his colleagues at the University of Texas at Dallas reported they had triggered the release of 2.45 MeV in gamma rays from a sample of Hafnium-178m2 by irradiating it with a second-hand dental X-ray machine with the sample of the isomer sitting on a styrofoam cup. Their report implied, even with the crude apparatus, an energy gain of sixty times break-even, which was more than a million times the rate predicted by nuclear theory, if triggering were possible at all. The result, if real, could have substantial technological consequences: the isomer could be used as a nuclear battery, which could store energy and release it on demand with a density which dwarfed that of any chemical battery and was only a couple of orders of magnitude less than a fission bomb. And, speaking of bombs, if you could manage to trigger a mass of hafnium all at once or arrange for it to self-trigger in a chain reaction, you could make a variety of nifty weapons out of it, including a nuclear hand grenade with a yield of two kilotons. You could also build a fission-free trigger for a thermonuclear bomb which would evade all of the existing nonproliferation safeguards which are aimed at controlling access to fissile material. These are the kind of things that get the attention of folks in that big five-sided building in Arlington, Virginia.

And so it came to pass, in a Pentagon bent on “transformational technologies” and concerned with emerging threats from potential adversaries, that in May of 2003 a Hafnium Isomer Production Panel (HIPP) was assembled to draw up plans for bulk production of the substance, with visions of nuclear hand grenades, clean bunker-busting fusion bombs, and even hafnium-powered bombers floating before the eyes of the out of the box thinkers at DARPA, who envisioned a two-year budget of USD30 million for the project—military science marches into the future. What's wrong with this picture? Well, actually rather a lot of things.

• No other researcher had been able to reproduce the results from the original experiment. This included a team of senior experimentalists who used the Advanced Photon Source at Argonne National Laboratory and state of the art instrumentation and found no evidence whatsoever for triggering of the hafnium isomer with X-rays—in two separate experiments.
• As noted above, well-understood nuclear theory predicted the yield from triggering, if it occurred, to be six orders of magnitude less than reported in Collins's paper.
• An evaluation of the original experiment by the independent JASON group of senior experts in 1999 determined the result to be “a priori implausible” and “inconclusive, at best”.
• A separate evaluation by the Institute for Defense Analyses concluded the original paper reporting the triggering results “was flawed and should not have passed peer review”.
• Collins had never run, and refused to run, a null experiment with ordinary hafnium to confirm that the very small effect he reported went away when the isomer was removed.
• James Carroll, one of the co-authors of the original paper, had obtained nothing but null results in his own subsequent experiments on hafnium triggering.
• Calculations showed that even if triggering were to be possible at the reported rate, the process would not come close to breaking even: more than six times as much X-ray energy would go in as gamma rays came out.
• Even if triggering worked, and some way were found to turn it into an energy source or explosive device, the hafnium isomer does not occur in nature and would have to be made by a hideously inefficient process in a nuclear reactor or particle accelerator, at a cost estimated at around a billion dollars per gram. The explosive in the nuclear hand grenade would cost tens of billions of dollars, compared to which highly enriched uranium and plutonium are cheap as dirt.
• If the material could be produced and triggering made to work, the resulting device would pose an extreme radiation hazard. Radiation is inverse to half-life, and the hafnium isomer, with a 31 year half-life, is vastly more radioactive than U-235 (700 million years) or Pu-239 (24,000 years). Further, hafnium isomer decays emit gamma rays, which are the most penetrating form of ionising nuclear radiation and the most difficult against which to shield. The shielding required to protect humans in the vicinity of a tangible quantity of hafnium isomer would more than negate its small mass and compact size.
• A hafnium explosive device would disperse large quantities of the unreacted isomer (since a relatively small percentage of the total explosive can react before the device is disassembled in the explosion). As it turns out, the half-life of the isomer is just about the same as that of Cesium-137, which is often named as the prime candidate for a “dirty” radiological bomb. One physicist on the HIPP (p. 176) described a hafnium weapon as “the mother of all dirty bombs”.
• And consider that hand grenade, which would weigh about five pounds. How far can you throw a five pound rock? What do you think about being that far away from a detonation with the energy of two thousand tons of TNT, all released in prompt gamma rays?

But bad science, absurd economics, a nonexistent phenomenon, damning evaluations by panels of authorities, lack of applications, and ridiculous radiation risk in the extremely improbable event of success pose no insurmountable barriers to a government project once it gets up to speed, especially one in which the relationships between those providing the funding and its recipients are complicated and unseemingly cozy. It took an exposé in the Washington Post Magazine by the author and subsequent examination in Congress to finally drive a stake through this madness—maybe. As of the end of 2005, although DARPA was out of the hafnium business (at least publicly), there were rumours of continued funding thanks to a Congressional earmark in the Department of Energy budget.

This book is a well-researched and fascinating look inside the defence underworld where fringe science feeds on federal funds, and starkly demonstrates how weird and wasteful things can get when Pentagon bureaucrats disregard their own science advisors and substitute instinct and wishful thinking for the tedious, but ultimately reliable, scientific method. Many aspects of the story are also quite funny, although U.S. taxpayers who footed the bill for this madness may be less amused. The author has set up a Web site for the book, and Carl Collins, who conducted the original experiment with the dental X-ray and styrofoam cup which incited the mania has responded with his own, almost identical in appearance, riposte. If you're interested in more technical detail on the controversy than appears in Weinberg's book, the Physics Today article from May 2004 is an excellent place to start. The book contains a number of typographical and factual errors, none of which are significant to the story, but when the first line of the Author's Note uses “sited” when “cited” is intended, and in the next paragraph “wondered” instead of “wandered”, you have to—wonder.

It is sobering to realise that this folly took place entirely in the public view: in the open scientific literature, university labs, unclassified defence funding subject to Congressional oversight, and ultimately in the press, and yet over a period of years millions in taxpayer funds were squandered on nonsense. Just imagine what is going on in highly-classified “black” programs.

June 2006 

Wilczek, Frank. Fantastic Realities. Singapore: World Scientific, 2006. ISBN 981-256-655-4.

The author won the 2004 Nobel Prize in Physics for his discovery of “asymptotic freedom” in the strong interaction of quarks and gluons, which laid the foundation of the modern theory of Quantum Chromodynamics (QCD) and the Standard Model of particle physics. This book is an anthology of his writing for general and non-specialist scientific audiences over the last fifteen years, including eighteen of his “Reference Frame” columns from Physics Today and his Nobel prize autobiography and lecture.

I had eagerly anticipated reading this book. Frank Wilczek and his wife Betsy Devine are co-authors of the 1988 volume Longing for the Harmonies, which I consider to be one of the best works of science popularisation ever written, and whose “theme and variation” structure I adopted for my contemporary paper “The New Technological Corporation”. Wilczek is not only a brilliant theoretician, he has a tremendous talent for explaining the arcana of quantum mechanics and particle physics in lucid prose accessible to the intelligent layman, and his command of the English language transcends pedestrian science writing and sometimes verges on the poetic, occasionally crossing the line: this book contains six original poems!

The collection includes five book reviews, in a section titled “Inspired, Irritated, Inspired”, the author's reaction to the craft of reviewing books, which he describes as “like going on a blind date to play Russian roulette” (p. 305). After finishing this 500 page book, I must sadly report that my own experience can be summed up as “Inspired, Irritated, Exasperated”. There is inspiration aplenty and genius on display here, but you're left with the impression that this is a quickie book assembled by throwing together all the popular writing of a Nobel laureate and rushed out the door to exploit his newfound celebrity. This is not something you would expect of World Scientific, but the content of the book argues otherwise.

Frank Wilczek writes frequently for a variety of audiences on topics central to his work: the running of the couplings in the Standard Model, low energy supersymmetry and the unification of forces, a possible SO(10) grand unification of fundamental particles, and lattice QCD simulation of the mass spectrum of mesons and hadrons. These are all fascinating topics, and Wilczek does them justice here. The problem is that with all of these various articles collected in one book, he does them justice again, again, and again. Four illustrations: the lattice QCD mass spectrum, the experimentally measured running of the strong interaction coupling, the SO(10) particle unification chart, and the unification of forces with and without supersymmetry, appear and are discussed three separate times (the latter four times) in the text; this gets tedious.

There is sufficient wonderful stuff in this book to justify reading it, but don't feel duty-bound to slog through the nth repetition of the same material; a diligent editor could easily cut at least a third of the book, and probably close to half without losing any content. The final 70 pages are excerpts from Betsy Devine's Web log recounting the adventures which began with that early morning call from Sweden. The narrative is marred by the occasional snarky political comment which, while appropriate in a faculty wife's blog, is out of place in an anthology of the work of a Nobel laureate who scrupulously avoids mixing science and politics, but still provides an excellent inside view of just what it's like to win and receive a Nobel prize.

August 2006 

Wilczek, Frank. The Lightness of Being. New York: Basic Books, 2008. ISBN 978-0-465-00321-1.

For much of its history as a science, physics has been about mass and how it behaves in response to various forces, but until very recently physics had little to say about the origin of mass: it was simply a given. Some Greek natural philosophers explained it as being made up of identical atoms, but then just assumed that the atoms somehow had their own intrinsic mass. Newton endowed all matter with mass, but considered its origin beyond the scope of observation and experiment and thus outside the purview of science. As the structure of the atom was patiently worked out in the twentieth century, it became clear that the overwhelming majority of the mass of atoms resides in a nucleus which makes up a minuscule fraction of its volume, later that the nucleus is composed of protons and neutrons, and still later that those particles were made up of quarks and gluons, but still physicists were left with no explanation for why these particles had the masses they did or, for that matter, any mass at all.

In this compelling book, Nobel Physics laureate and extraordinarily gifted writer Frank Wilczek describes how one of the greatest intellectual edifices ever created by the human mind: the drably named “standard model” of particle physics, combined with what is almost certainly the largest scientific computation ever performed to date (teraflop massively parallel computers running for several months on a single problem), has finally produced a highly plausible explanation for the origin of the mass of normal matter (ourselves and everything we have observed in the universe), or at least about 95% of it—these matters, and matter itself, always seems to have some more complexity to tease out.

And what's the answer? Well, the origin of mass is the vacuum, and its interaction with fields which fill all of the space in the universe. The quantum vacuum is a highly dynamic medium, seething with fluctuations and ephemeral virtual particles which come and go in instants which make even the speed of present-day computers look like geological time. The interaction of this vacuum with massless quarks produces, through processes explained so lucidly here, around 95% of the mass of the nucleus of atoms, and hence what you see when stepping on the bathroom scale. Hey, if you aren't happy with that number, just remember that 95% of it is just due to the boiling of the quantum vacuum. Or, you could go on a diet.

This spectacular success of the standard model, along with its record over the last three decades in withstanding every experimental test to which it has been put, inspires confidence that, as far as it goes, it's on the right track. But just as the standard model was consolidating this triumph, astronomers produced powerful evidence that everything it explains: atoms, ourselves, planets, stars, and galaxies—everything we observe and the basis of all sciences from antiquity to the present—makes up less than 5% of the total mass of the universe. This discovery, and the conundrum of how the standard model can be reconciled with the equally-tested yet entirely mathematically incompatible theory of gravitation, general relativity, leads the author into speculation on what may lie ahead, how what we presently know (or think we know) may be a piece in a larger puzzle, and how experimental tests expected within the next decade may provide clues and open the door to these larger theories. All such speculation is clearly labeled, but it is proffered in keeping with what he calls the Jesuit Credo, “It is more blessed to ask forgiveness than permission.”

This is a book for the intelligent layman, and a superb twenty page glossary is provided for terms used in the text with which the reader may be unfamiliar. In fact, the glossary is worth reading in its own right, as it expands on many subjects and provides technical details absent in the main text. The end notes are also excellent and shouldn't be missed. One of the best things about this book, in my estimation, is what is missing from it. Unlike so many physicists writing for a popular audience, Wilczek feels no need whatsoever to recap the foundations of twentieth century science. He assumes, and I believe wisely, that somebody who picks up a book on the origin of mass by a Nobel Prize winner probably already knows the basics of special relativity and quantum theory and doesn't need to endure a hundred pages recounting them for the five hundredth time before getting to the interesting stuff. For the reader who has wandered in without this background knowledge, the glossary will help, and also direct the reader to introductory popular books and texts on the various topics.

March 2009 

Woit, Peter. Not Even Wrong. London: Jonathan Cape, 2006. ISBN 0-224-07605-1.

Richard Feynman, a man about as difficult to bamboozle on scientific topics as any who ever lived, remarked in an interview (p. 180) in 1987, a year before his death:

…I think all this superstring stuff is crazy and it is in the wrong direction. … I don't like that they're not calculating anything. I don't like that they don't check their ideas. I don't like that for anything that disagrees with an experiment, they cook up an explanation—a fix-up to say “Well, it still might be true.”

Feynman was careful to hedge his remark as being that of an elder statesman of science, who collectively have a history of foolishly considering the speculations of younger researchers to be nonsense, and he would have almost certainly have opposed any effort to cut off funding for superstring research, as it might be right, after all, and should be pursued in parallel with other promising avenues until they make predictions which can be tested by experiment, falsifying and leading to the exclusion of those candidate theories whose predictions are incorrect.

One wonders, however, what Feynman's reaction would have been had he lived to contemplate the contemporary scene in high energy theoretical physics almost twenty years later. String theory and its progeny still have yet to make a single, falsifiable prediction which can be tested by a physically plausible experiment. This isn't surprising, because after decades of work and tens of thousands of scientific publications, nobody really knows, precisely, what superstring (or M, or whatever) theory really is; there is no equation, or set of equations from which one can draw physical predictions. Leonard Susskind, a co-founder of string theory, observes ironically in his book The Cosmic Landscape (March 2006), “On this score, one might facetiously say that String Theory is the ultimate epitome of elegance. With all the years that String Theory has been studied, no one has ever found a single defining equation! The number at present count is zero. We know neither what the fundamental equations of the theory are or even if it has any.” (p. 204). String theory might best be described as the belief that a physically correct theory exists and may eventually be discovered by the research programme conducted under that name.

From the time Feynman spoke through the 1990s, the goal toward which string theorists were working was well-defined: to find a fundamental theory which reproduces at the low energy limit the successful results of the standard model of particle physics, and explains, from first principles, the values of the many (there are various ways to count them, slightly different—the author gives the number as 18 in this work) free parameters of that theory, whose values are not predicted by any theory and must be filled in by experiment. Disturbingly, theoretical work in the early years of this century has convinced an increasing number of string theorists (but not all) that the theory (whatever it may turn out to be), will not predict a unique low energy limit (or “vacuum state”), but rather an immense “landscape” of possible universes, with estimates like 10¹⁰⁰ and 10⁵⁰⁰ and even more bandied around (by comparison, there are only about 10⁸⁰ elementary particles in the entire observable universe—a minuscule number compared to such as these). Most of these possible universes would be hideously inhospitable to intelligent life as we know and can imagine it (but our imagination may be limited), and hence it is said that the reason we find ourselves in one of the rare universes which contain galaxies, chemistry, biology, and the National Science Foundation is due to the anthropic principle: a statement, bordering on tautology, that we can only observe conditions in the universe which permit our own existence, and that perhaps either in a “multiverse” of causally disjoint or parallel realities, all the other possibilities exist as well, most devoid of observers, at least those like ourselves (triune glorgs, feeding on bare colour in universes dominated by quark-gluon plasma would doubtless deem our universe unthinkably cold, rarefied, and dead).

But adopting the “landscape” view means abandoning the quest for a theory of everything and settling for what amounts to a “theory of anything”. For even if string theorists do manage to find one of those 10¹⁰⁰ or whatever solutions in the landscape which perfectly reproduces all the experimental results of the standard model (and note that this is something nobody has ever done and appears far out of reach, with legitimate reasons to doubt it is possible at all), then there will almost certainly be a bewildering number of virtually identical solutions with slightly different results, so that any plausible experiment which measures a quantity to more precision or discovers a previously unknown phenomenon can be accommodated within the theory simply by tuning one of its multitudinous dials and choosing a different solution which agrees with the experimental results. This is not what many of the generation who built the great intellectual edifice of the standard model of particle physics would have considered doing science.

Now if string theory were simply a chimæra being pursued by a small band of double-domed eccentrics, one wouldn't pay it much attention. Science advances by exploring lots of ideas which may seem crazy at the outset and discarding the vast majority which remain crazy after they are worked out in more detail. Whatever remains, however apparently crazy, stays in the box as long as its predictions are not falsified by experiment. It would be folly of the greatest magnitude, comparable to attempting to centrally plan the economy of a complex modern society, to try to guess in advance, by some kind of metaphysical reasoning, which ideas were worthy of exploration. The history of the S-matrix or “bootstrap” theory of the strong interactions recounted in chapter 11 is an excellent example of how science is supposed to work. A beautiful theory, accepted by a large majority of researchers in the field, which was well in accord with experiment and philosophically attractive, was almost universally abandoned in a few years after the success of the quark model in predicting new particles and the stunning deep inelastic scattering results at SLAC in the 1970s.

String theory, however, despite not having made a single testable prediction after more than thirty years of investigation, now seems to risk becoming a self-perpetuating intellectual monoculture in theoretical particle physics. Among the 22 tenured professors of theoretical physics in the leading six faculties in the United States who received their PhDs after 1981, fully twenty specialise in string theory (although a couple now work on the related brane-world models). These professors employ graduate students and postdocs who work in their area of expertise, and when a faculty position opens up, may be expected to support candidates working in fields which complement their own research. This environment creates a great incentive for talented and ambitious students aiming for one the rare permanent academic appointments in theoretical physics to themselves choose string theory, as that's where the jobs are. After a generation, this process runs the risk of operating on its own momentum, with nobody in a position to step back and admit that the entire string theory enterprise, judged by the standards of genuine science, has failed, and does not merit the huge human investment by the extraordinarily talented and dedicated people who are pursuing it, nor the public funding it presently receives. If Edward Witten believes there's something still worth pursuing, fine: his self-evident genius and massive contributions to mathematical physics more than justify supporting his work. But this enterprise which is cranking out hundreds of PhDs and postdocs who are spending their most intellectually productive years learning a fantastically complicated intellectual structure with no grounding whatsoever in experiment, most of whom will have no hope of finding permanent employment in the field they have invested so much to aspire toward, is much more difficult to justify or condone.

The problem, to state it in a manner more inflammatory than the measured tone of the author, and in a word of my choosing which I do not believe appears at all in his book, is that contemporary academic research in high energy particle theory is corrupt. As is usually the case with such corruption, the root cause is socialism, although the look-only-left blinders almost universally worn in academia today hides this from most observers there. Dwight D. Eisenhower, however, twigged to it quite early. In his farewell address of January 17th, 1961, which academic collectivists endlessly cite for its (prescient) warning about the “military-industrial complex”, he went on to say, although this is rarely quoted,

In this revolution, research has become central; it also becomes more formalized, complex, and costly. A steadily increasing share is conducted for, by, or at the direction of, the Federal government.

Today, the solitary inventor, tinkering in his shop, has been over shadowed by task forces of scientists in laboratories and testing fields. In the same fashion, the free university, historically the fountainhead of free ideas and scientific discovery, has experienced a revolution in the conduct of research. Partly because of the huge costs involved, a government contract becomes virtually a substitute for intellectual curiosity. For every old blackboard there are now hundreds of new electronic computers.

The prospect of domination of the nation's scholars by Federal employment, project allocations, and the power of money is ever present and is gravely to be regarded.

And there, of course, is precisely the source of the corruption. This enterprise of theoretical elaboration is funded by taxpayers, who have no say in how their money, taken under threat of coercion, is spent. Which researchers receive funds for what work is largely decided by the researchers themselves, acting as peer review panels. While peer review may work to vet scientific publications, as soon as money becomes involved, the disposition of which can make or break careers, all the venality and naked self- and group-interest which has undone every well-intentioned experiment in collectivism since Robert Owen comes into play, with the completely predictable and tediously repeated results. What began as an altruistic quest driven by intellectual curiosity to discover answers to the deepest questions posed by nature ends up, after a generation of grey collectivism, as a jobs program. In a sense, string theory can be thought of like that other taxpayer-funded and highly hyped program, the space shuttle, which is hideously expensive, dangerous to the careers of those involved with it (albeit in a more direct manner), supported by a standing army composed of some exceptional people and a mass of the mediocre, difficult to close down because it has carefully cultivated a constituency whose own self-interest is invested in continuation of the program, and almost completely unproductive of genuine science.

One of the author's concerns is that the increasingly apparent impending collapse of the string theory edifice may result in the de-funding of other promising areas of fundamental physics research. I suspect he may under-estimate how difficult it is to get rid of a government program, however absurd, unjustified, and wasteful it has become: consider the space shuttle, or mohair subsidies. But perhaps de-funding is precisely what is needed to eliminate the corruption. Why should U.S. taxpayers be spending on the order of thirty million dollars a year on theoretical physics not only devoid of any near- or even distant-term applications, but also mostly disconnected from experiment? Perhaps if theoretical physics returned to being funded by universities from their endowments and operating funds, and by money raised from patrons and voluntarily contributed by the public interested in the field, it would be, albeit a much smaller enterprise, a more creative and productive one. Certainly it would be more honest. Sure, there may be some theoretical breakthrough we might not find for fifty years instead of twenty with massive subsidies. But so what? The truth is out there, somewhere in spacetime, and why does it matter (since it's unlikely in the extreme to have any immediate practical consequences) how soon we find it, anyway? And who knows, it's just possible a research programme composed of the very, very best, whose work is of such obvious merit and creativity that it attracts freely-contributed funds, exploring areas chosen solely on their merit by those doing the work, and driven by curiosity instead of committee group-think, might just get there first. That's the way I'd bet.

For a book addressed to a popular audience which contains not a single equation, many readers will find it quite difficult. If you don't follow these matters in some detail, you may find some of the more technical chapters rather bewildering. (The author, to be fair, acknowledges this at the outset.) For example, if you don't know what the hierarchy problem is, or why it is important, you probably won't be able to figure it out from the discussion here. On the other hand, policy-oriented readers will have little difficulty grasping the problems with the string theory programme and its probable causes even if they skip the gnarly physics and mathematics. An entertaining discussion of some of the problems of string theory, in particular the question of “background independence”, in which the string theorists universally assume the existence of a background spacetime which general relativity seems to indicate doesn't exist, may be found in Carlo Rovelli's "A Dialog on Quantum Gravity". For more technical details, see Lee Smolin's Three Roads to Quantum Gravity. There are some remarkable factoids in this book, one of the most stunning being that the proposed TeV class muon colliders of the future will produce neutrino (yes, neutrino) radiation which is dangerous to humans off-site. I didn't believe it either, but look here—imagine the sign: “DANGER: Neutrino Beam”!

A U.S. edition is scheduled for publication at the end of September 2006. The author has operated the Not Even Wrong Web log since 2004; it is an excellent source for news and gossip on these issues. The unnamed “excitable … Harvard faculty member” mentioned on p. 227 and elsewhere is Luboš Motl (who is, however, named in the acknowledgements), and whose own Web log is always worth checking out.

June 2006 

Wolfram, Stephen. A New Kind of Science. Champaign, IL: Wolfram Media, 2002. ISBN 1-57955-008-8.

The full text of this book may now be read online.

August 2002 

Wright, Lawrence. Going Clear. New York: Alfred A. Knopf, 2013. ISBN 978-0-307-70066-7.

In 2007 the author won a Pulitzer Prize for The Looming Tower, an exploration of the origins, structure, and activities of Al-Qaeda. In the present book, he dares to take on a really dangerous organisation: the Church of Scientology. Wright delves into the tangled history of its founder, L. Ron Hubbard, and the origins of the church, which, despite having occurred within the lifetimes of many readers of the book, seem cloaked in as much fog, misdirection, and conflicting claims as those of religions millennia older. One thing which is beyond dispute to anybody willing to examine the objective record is that Hubbard was a masterful confidence man—perhaps approaching the magnitude of those who founded other religions. This was apparent well before he invented Dianetics and Scientology: he moved into Jack Parsons' house in Pasadena, California, and before long took off with Parsons' girlfriend and most of his savings with a scheme to buy yachts in Florida and sell them in California. Hubbard's military career in World War II is also murky in the extreme: military records document that he was never in combat, but he spun a legend about chasing Japanese submarines off the coast of Oregon, being injured, and healing himself through mental powers.

One thing which nobody disputes is that Hubbard was a tremendously talented and productive writer of science fiction. He was a friend of Robert A. Heinlein and a regular correspondent with John W. Campbell. You get the sense in this book that Hubbard didn't really draw a hard and fast line between the fanciful stories he wrote for a living and the actual life he lived—his own biography and persona seem to have been as much a fabrication as the tales he sold to the pulp magazines.

On several occasions Hubbard remarked that the way to make a big pile of money was to start a religion. (It is often said that he made a bar bet with Heinlein that he could start a religion, but the author's research concludes this story is apocryphal. However, Wright identifies nine witnesses who report hearing Hubbard making such a remark in 1948 or 1949.) After his best-selling book Dianetics landed him in trouble with the scientific and mental health establishment, he decided to take his own advice and re-instantiate it as a religion. In 1954, Scientology was born.

Almost immediately, events took a turn into high weirdness. While the new religion attracted adherents, especially among wealthy celebrities in Hollywood, it also was the object of ridicule and what Scientologists viewed as persecution. Hubbard and his entourage took to the sea in a fleet of ships, attended by a “clergy” called Sea Org, who signed billion year contracts of allegiance to Scientology and were paid monastic subsistence salaries and cut off from contact with the world outside Scientology. Hubbard continued to produce higher and higher levels of revelation for his followers, into which they could be initiated for a formidable fee.

Some of this material was sufficiently bizarre (for example, the Xenu [or Xemu] story, revealed in 1967) that adherents to Scientology walked away, feeling that their religion had become bad space opera. That was the first reaction of Paul Haggis, whose 34 years in Scientology are the foundation of this narrative. And yet Haggis did not leave Scientology after his encounter with Xenu: he eventually left the church in 2009 after it endorsed a California initiative prohibiting same-sex marriage.

There is so much of the bizarre in this narrative that you might be inclined to dismiss it as tabloid journalism, had not the author provided a wealth of source citations, many drawn from sworn testimony in court and evidence in legal proceedings. In the Kindle edition, these links are live and can be clicked to view the source documents.

From children locked in chain lockers on board ship; to adults placed in detention in “the hole”; to special minders assigned to fulfill every whim of celebrity congregants such as John Travolta and Tom Cruise; to blackmail, lawfare, surveillance, and harassment of dissidents and apostates; to going head-to-head with the U.S. Internal Revenue Service and winning a tax exemption from them in 1993, this narrative reads like a hybrid of the science fiction and thriller genres, and yet it is all thoroughly documented. In end-note after end-note, the author observes that the church denies what is asserted, then provides multiple source citations to the contrary.

This is a remarkably even-handed treatment of a religion that many deem worthy only of ridicule. Yes, Scientologists believe some pretty weird things, but then so do adherents of “mainstream” religions. Scientology's sacred texts seem a lot like science fiction, but so do those of the Mormons, a new religion born in America a century earlier, subjected to the same ridicule and persecution the Scientologists complain of, and now sufficiently mainstream that a member could run for president of the U.S. without his religion being an issue in the campaign. And while Scientology seems like a mix of science fiction and pseudo-science, some very successful people have found it an anchor for their lives and attribute part of their achievement to it. The abuses documented here are horrific, and the apparent callousness with which money is extracted from believers to line the pockets of those at the top is stunning, but then one can say as much of a number of religions considered thoroughly respectable by many people.

I'm a great believer in the market. If Scientology didn't provide something of value to those who believe in it, they wouldn't have filled its coffers with more than a billion dollars (actually, nobody knows the numbers: Scientology's finances are as obscure as its doctrines). I'll bet the people running it will push the off-putting weird stuff into the past, shed the abusive parts, and morph into a religion people perceive as no more weird than the Mormons. Just as being a pillar of the LDS church provides a leg up in some communities in the Western U.S., Scientology will provide an entrée into the world of Hollywood and media. And maybe in 2112 a Scientologist will run for president of the Reunited States and nobody will make an issue of it.

February 2013 

Yates, Raymond F. Atomic Experiments for Boys. New York: Harper & Brothers, 1952. LCCN 52-007879.

This book is out of print. You may be able to locate a copy through abebooks.com; that's where I found mine.

April 2002