Copyright 1993, Journal of Parapsychology. Reproduced with permission.
To purchase a complete issue write Journal of Parapsychology, 402 N. Buchanan
Blvd., Durham, NC 27701, USA (journal@rhine.org). For copies of complete articles, write The Genuine Article, ISI, 3501 Market St., Philadelphia, PA 19104 USA.
OBSERVATION OF A PSYCHOKINETIC
EFFECT UNDER HIGHLY CONTROLLED
CONDITIONS
(Originally published in Journal of Parapsychology, Vol. 57, Dec. 1993)
ABSTRACT: The author summarizes five experiments in which he studied the
psychokinetic (PK) effect
(the mental influence on the outcome of chance processes) under tight
supervision by independent observers. Through the use of prerecorded random events as
targets, the observers could evaluate the results independently, without having to trust the
reliability of the author or his equipment. The total of these five studies, which represent
all the work done under external supervision, produced an effect deviating by
3.67 standard deviations from chance expectancy. The odds against such an outcome are
about 8,000 to 1. Thus, the results support the extstence of a PK effect on prerecorded
random events, in agreement with previous experiments. The observed PK effect is
inconsistent with current quantum theory. It shows that the theory is not correct when
applied to systems that include human subjects. Furthermore, the existence of a weak
mental effect on the outcome of chance events cautions the physicist to be
careful in the interpretation of results that are based on relatively few
chance events.
A psychokinetic (PK) effect - a mental influence on the outcome of chance
processes - was first reported by
Louisa and J.B. Rhine
(Rhine & Rhine, 1943) from experiments with dice. Through the introduction
of electronic
random number generators based on quantum randomness
(Schmidt, 1971), the experiments became more easily accessible and even more
challenging to physicists. Today, a large number of successful PK
experiments with random number generators have been reported
(Radin and
Nelson, 1989). It has not yet been possible, however, to stabilize
and strengthen the statistically weak effects so that they can be easily
demonstrated on demand.
The discovery of PK effects on prerecorded random events (Schmidt, 1976)
did not make the gathering of data less arduous, but it permitted the
inclusion of independent observers who, with little investment of time and
effort, could obtain first-hand evidence for any PK effects that might occur.
All five experiments to be discussed here included such independent observers.
In a typical PK experiment, a random number generator produces a binary
random sequence that the subject tries to bias in a certain manner. Let
us take, for example, the case where the random generator produces in each
test run a sequence of 100 binary events displayed as a sequence of 100 red
(for a 0-bit) and green (for a 1-bit) light flashes, while the subject is
instructed to mentally enforce the appearance of more red than green flashes.
The sequence of red and green signals is stored on floppy disk, and a score
that is measured by the difference between the numbers of red and green
signals is displayed and recorded at the end of the run (see Figure 1).
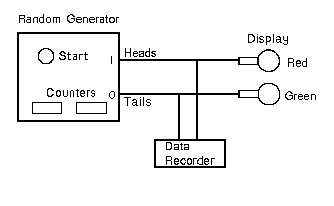
Figure 1. PK experiment with random events
The arrangement for an experiment with prerecorded random events (see
Figure 2) is similar, but there is a time delay between the generation of
the random events and their display to the subject.
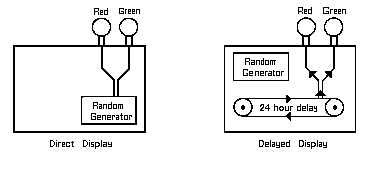
Figure 2. PK experiment with prerecorded events
First, the random signals for a large number of test runs are generated
and recorded on floppy disk. Days or months later, the stored signals are
translated by the computer into a corresponding sequence of
red and green light flashes while the subject tries to mentally enforce the
appearance of more red than green signals.
Experiments have shown that selected subjects can succeed in this
arrangement (Schmidt, 1976, 1987), provided that the prerecorded events
have not been inspected by anybody before the subject makes the
PK effort.
To let an independent observer participate in the experiment, we prerecord
the bit sequences for all test runs planned for the experiment, and we let
a computer make a printout of the scores for all the test runs. Being
careful that nobody can observe the scores, we send a sealed copy of the
printout to the independent observer. Leaving the printout sealed, the
independent observer randomly specifies for each test run whether the
subject's PK effort should be aimed at a high score (excess of red signals
in the example) or a low score (excess of green signals).
In the subsequent PK test sessions, the subject follows for each test run
the independent observer's assignments, aiming for an excess of red
or green signals, respectively.
At the end of the experiment, the independent observer opens the sealed
printouts. If the subject's effort was successful, the independent observer
can confirm this first-hand by a tendency of the scores to point in the
directions (positive or negative) that he had randomly specified.
Because the independent observer had randomly assigned the directions, he
or she can be certain that no such systematic tendency should occur (in the
absence of the claimed anomaly). Using an appropriate statistical method,
the independent observer can assess the significance of such a tendency
without having to consider the reliability of the experimenter and his
procedures.
Test Arrangement with Distant Subjects
The five experiments under discussion followed this general outline with
minor variations. The most notable difference was the use of a variety of
different feedback options and a test arrangement permitting subjects to
work at home at their convenience instead of coming to the laboratory.
In the first experiment, I mailed to the participants small computers that
could be connected to TV sets. During a run of typically one minute,
the subject saw a pendulum swing on the screen, with randomly varying
amplitudes. The amplitude variations were dictated by a predetermined
binary random sequence of zeros and ones. After each half-cycle of the
swinging pendulum, the computer read the next bit and, for a 1 or a 0,
respectively, increased or decreased the amplitude (if possible within
the available range). Depending on the target assignment, the subject
tried either to make the pendulum swing with maximal amplitude over the
whole screen, or to keep the swinging confined to a narrow region at the
center of the screen.
The last two experiments provided a similar display, without the use of a
TV screen. The test machine showed a row of 27 lamps on which the subject
saw a light swinging back and forth. The system was controlled by a
microprocessor chip that, in addition to the test program, held the
prerecorded random events that determined the swing pattern.
Most of the subjects were not aware that this was a PK test with prerecorded
events, because it looked like an ordinary PK test in which the subject
tries to affect the display in a certain manner and receives a success
score at the end of a run.
In Experiments 2 and 3, the subjects received only auditory feedback. In
a typical case, the subject's task was to extend or to shorten tone
intervals of random duration, prerecorded on cassette tapes. These tapes
were mailed to the subjects with appropriate instructions.
These experiments
were particularly simple to set up because only cassette tapes had to be
mailed out instead of expensive microprocessor-controlled test machines.
There was a possible disadvantage, however, insofar as many subjects
noticed that this was not a standard PK test. They wondered how they
could affect the tones, which had already been recorded on the tape, and
I doubt whether the explanations I was able to provide gave them much
comfort.
More information about the forms of feedback used, as well as other details,
is provided in the Appendix.
Proposed Interpretations of PK Effects on Prerecorded Data
To our naive intuition, PK effects under time displacement may appear
particularly puzzling. With the random events already generated and
recorded, we feel that the subject's mental effort comes too late to have
an effect. Let us remember, however, that our naive intuition is equally
at a loss in explaining better known psi phenomena such as clairvoyance
and precognition.
One logically consistent viewpoint is that the mental effort of the
subject in the test session has a retroactive effect on the moment the
random events were generated (Schmidt, 1975, 1978).
One might want random
to say that the random generator "senses" that a subject will later make a
PK effort, and behaves accordingly. A similar process, with the time order
between cause and effect inverted, may also be found in precognition.
Another viewpoint (Schmidt, 1982,
1984) is based on the idea of quantum
theory that only those happenings that have been observed are physically
real. In this case, the random events recorded on disk, as well as the
corresponding printed scores, are not yet real; nature has not yet decided
on the outcome until somebody has looked at the outcome. Thus it is only
at the moment of observation by the PK subject that nature decides for
"red" or "green." Then, the subject's mental efrort does not have to reach
into the past, because the "collapse of the state vector," nature's final
decision for one of several possible branches of reality, occurs during the
test session.
The Effect of Preinspection of the Prerecorded Data
From the viewpoint just mentioned, the PK effects should disappear if
somebody has looked at the prerecorded scores previous to the PK test
session. In this scenario, the preinspection would collapse the state
vector so that the subject would find nature in a decided state, with no
opening left for PK to act. For this reason, the initial PK experiments
with prerecorded events precluded such preinspection. On the other hand,
experiments with preinspected prerecorded data are most interesting because
they might discriminate between the two mentioned viewpoints.
Two previous experiments were concerned with the effects of preinspection.
In one experiment (Schmidt, 1985) where the preinspection was very thorough
(letting the preinspector experience the scores as vividly as they were
later experienced by the PK subject), the preinspection inhibited the
subsequent PK effort. (This result should be taken with some caution until
it has been confirmed by other investigators.) Another group of experiments
has indicated that the preinspection of the prerecorded data does not
inhibit the subsequent PK effort if the preinspection does not provide
immediate information about the resulting scores. These experiments
(Schmidt, 1981, and the present Experiment 1) worked with prerecorded and
preinspected random seed numbers as follows.
Use of Prerecorded Random Seed Numbers in the First Experiment
In the arrangements described so far, the random bits on which the
subjects directed their PK efforts were individually generated and stored.
In the first experiment, however, a true random number generator was used
only to generate, for each test run, one 19-bit seed number. A quasi-random
algorithm then derived from this seed number the larger number of bits
required for the test run. One might feel that the reduced amount of
randomness, entering only through the random seed number, gave the subject
fewer chances to succeed. On the other hand, there are theoretical models
that predict the same success rate as in the earlier arrangement
(Schmidt, 1975, 1978). Furthermore, previous studies have shown that,
indeed, PK tests with prerecorded seed numbers can produce PK effects
(Schmidt, 1981), and that the PK effects even persist when the seed numbers
have been observed before the PK session. Note that the observer of a seed
number receives no direct information on the resulting score, unless he
works through the complex algorithm that derives the score from the seed
number.
At the start of the first experiment, the experimenter generated and
preinspected lists of random 6-digit seed numbers. The independent
observers obtained an open printout of these seed numbers, as well as the
information about how to derive the scores from the seed numbers at the
final stage of the experiment. Thus, the open list of seed numbers was
equivalent to the sealed list of scores provided in the other experiments.
The independent observers gave a random target assignment to each printed
seed number, requesting a high or low resulting score, and returned the
assignments to the experimenter.
A practical advantage of this arrangement was that no prerecorded data had
to be stored in the test device. Instead, at the start of each test run,
the subject typed the next seed number from the prepared list of random
numbers into the test computer. From this list, the computer calculated
and consecutively displayed the resulting binary sequence, while the subject
made a mental effort in the specified direction; and, at the end, the
computer displayed the final score.
At the end of the whole experiment, the independent observers typed the seed
numbers into an initially supplied test computer (or used a computer
algorithm, also supplied) to derive the scores from the seed numbers and
check the results.
The positive results obtained under these conditions need not invalidate the
viewpoint of our state-vector-collapse model, but they restrict the kind of
observations that do collapse the state vector and force nature to decide
between different possible branches of reality.
Statistical Design of the Five Experiments
The five experiments used different subject populations, different
psychological approaches, and a variety of feedback displays. This made
the experiments more interesting for experimenter and subjects. On the
other hand, the overriding goal of all experiments was to present evidence
of psi effects to the independent observers; and for the independent
observers much of this variety was irrelevant and not even visible.
A certain inconvenience for the experimenter is the need to specify the
length of an experiment in advance in order to avoid the well-known problems
connected with "optional stopping." In the present experiments this
inconvenience was alleviated by the following method.
Each of the five experiments was subdivided into a prespecified number
(n) of "units" (see Table 1), where each unit represented a
mini-experiment that could be evaluated (by a prespecified method) in
terms of a z value measuring the deviation of the result from chance
in units of one standard deviation, with positive values indicating a
deviation in the target direction.
TABLE 1
NUMBER (n) OF UNITS AND NAMES OF THE INDEPENDENT
OBSERVERS FOR THE FIVE EXPERIMENTS
From the z values of the individual units z1, z2,...,zn,
a final z value for the experiment was derived as
z = (z1 + z2 + ... + zn) / sqrt(n).
Whereas the number (n) of units of the whole experiment had to be
specified at the start, the length and other details about a unit had to be
specified (and to be communicated to the independent observers) only at the
start of this unit. This gave the experimenter some flexibility in
adjusting the length of the next unit to fit the available subjects and the
available time.
At the start of a unit, the experimenter and independent observer agreed on
the evaluation method, and then the independent observer received the score
printout, which also specified the length of the unit.
The independent observer, in turn, sent the target assignments to the
experimenter, and the test sessions could begin. At the end, the
experimenter and the independent observer separately evaluated the results
from the unit. (Details about the evaluation methods are given in the
section on Evaluation of the Different Units.)
Differences in the Feedback and in the Score Definition
For different kinds of feedback, providing different PK tasks, the score of
a run was defined such that this score reasonably reflected the subject's
success in the PK effort. Let us discuss this for the three major classes
of feedback that were used in the experiments:
1. One-dimensional unrestricted random walk. Consider a long linear
string of lamps with the center lamp lighted at the start. A binary-bit
sequence moves the light, one step at a time, to the right for a 1 and to
the left for a 0. The subject's task is to move the light as far as possible
to the right. Then a score (for the independent observer's printout) can
be defined in the same manner as in the example previously given, as the
difference between the numbers of 1s and 0s in the sequence. Because the
length of the lamp string is limited, the light is reset to the center
whenever it reaches a side.
2. One-dimensional random walk with two boundaries. Consider as an
example a linear string of seven lamps. Starting with the center lamp
lighted, each 1 or 0 moves the light one step to the right or left,
respectively, whereas the light stays stationary when the move would push
it beyond the seven-lamp range. The subject's task is to move the light
to the specified side and to keep it there as much as possible.
Let the positions of the lamps from left to right be given by x =
-3,-2,...,+3; and let x(n) be the light position after the nth
step. Then we can define the score, proportional to the average location
of the light, as
Score = x(l) + x(2) + x(N),
where N is the total number of steps.
Many of the units used a slight modification of this display, in which the
subject saw a pendulum swing with seven different amplitudes. After each
half-cycle the amplitude A = x(n) + 3 could increase or decrease by
one step, subject to the upper and lower limits. The subject's aim was
an average high or low amplitude.
3. Random time intervals. An interesting task for the subject is the
extension or the shortening of tones of random duration. To digitally
produce a random time interval, one can generate random numbers in
the range from 0 to (M - 1) at a regular rate and terminate the time
interval after a 0 is generated. The probability for an interval length of
m steps (m = 1,2,...) is given by
P(M)=pq^(M-1) with p=1/M, q= 1-P.
For reasonably large M values, (for example, M = 32), the time
intervals appear practically continuously variable, with the same statistics
as the time intervals between signals from a Geiger counter exposed to a
weak radioactive source.
If a subject tries to extend the durations of n time intervals in a
test run, the score can be defined as
Score = L(1) + ... + L(n),
where L(n) is the duration (in steps) of the nth interval.
Channeling the PK Effort in the Desired Direction
For units using the first two classes of feedback, the scores were printed
into the sealed list for the independent observer, who in turn randomly
assigned a target direction for each score. It was the experimenter's task
to direct the subject's PK effort in the assigned direction, consistent
with a high or low score, respectively. For this purpose, in principle,
the experimenter could have provided the subject with the target list
specifying the direction of the PK effort for each run. This was done in
Unit(1,1), the first unit of the first experiment. However, the frequent
switching in the target directions, with the need for mental readjustment,
as well as the need to keep track of the target list, appeared undesirable
to most subjects.
For the later units, therefore, the experimenter changed the original
bit-sequences from which the scores were printed into a secondary
bit-sequence for which the bits corresponding to runs with low-score
assignment were inverted (Os and 1s interchanged). Note that an inversion
of the bits in a run inverts the sign of the corresponding score. The
secondary bit-sequence was stored in the test machine used by the subject,
so that the secondary sequence determined the display during the run and
the (secondary) score seen by the subject. In order to succeed, the
subjects no longer needed to consult the assignment list. Rather, they
could consistently aim for high (secondary) scores shown at the end of
each run.
As an added convenience for the subject, the display during the run could
be inverted by the flipping of a switch so that success indicated by high
secondary scores could be associated, not only by motion to the right or
high swing-amplitudes, but also by motion to the left or low
swing-amplitudes. Thus the subject could freely set the ostensible aim
that seemed most attractive for the moment.
For units using the third class of feedback, the situation was different.
There, the lengths of the generated random intervals were prerecorded in
the form of binary numbers, but the durations of the intervals (long or
short) could not be inverted by inverting the bits in some binary sequence.
Furthermore, it seemed psychologically important that the subjects should
work consistently with the same target direction; for example, long
intervals.
Therefore the experimenter set a fixed target direction at the start and
let the independent observer's assignment enter as follows: Each test run
was based on a set of prerecorded random numbers (specifying the lengths of
the random intervals) with the score equal to the sum of these random
numbers. For each test run, the experimenter prepared 10 such sets of
numbers and inserted the corresponding scores into one line of the
independent observer's printout. The independent observer then randomly
decided which of the 10 entries in each line the PK effort should be
directed on to so as to make this number larger than the other 9
"control data." Accordingly, the experimenter loaded the specified data set
into the test machine which later displayed the data set (in the form of
random time intervals) to the subject.
In order to evaluate the results, the independent observer simply
rank-ordered the scores in each line and checked whether the selected scores
had a tendency to exceed the other control scores.
Evaluation of the Different Units by the Independent Observers
For the majority of the units (except the units using random time
intervals), the independent observers had specified the target assignments,
that is, high or low values for the scores printed in the sealed list.
The question was whether the values found after unsealing the lists tended
in the specified directions. In Experiments 1 to 4, a rank order test was
used to measure such a possible tendency and to translate it into a z
value. This nonparametric test made no assumptions about the distribution
of the data supplied by the experimenter (for details, see
Schmidt, Morris, and Rudolph, 1986). Before the
start of Experiment 5, the experimenter had found an equally valid but
conceptually and practically simpler evaluation method, which was then used
for Experiment 5, giving essentially the same result as the previously
used method.
To explain the simpler method, consider, for example, a unit with 100
printed scores, S(1), S(2),... S(100). From this score sequence,
a secondary sequence, S'(1), S'(2),...,S'(100), is derived by
inverting the signs of all scores S(n) that received a "low score"
assignment. PK success is now indicated by a tendency of the numbers
S'(n) toward positive values. We base our evaluation on the sum
V= S'(1) + S'(2) + ... + S'(100).
For any given set of values S(n), because of the random inversion
of the signs in going from S(n) to S'(n), the sum V is
a random variable with expectation value V* = 0 and with the variance
(V*)^2 = S(1)^2 + S(2)^2 + ... + S(100)^2.
This is true under the null hypothesis, in the absence of PK effects.
Because of the large number of contributing terms, the random variable
V has near normal distribution, and we can measure the significance
of a possible PK effect in terms of the deviation of V from chance
in terms of one standard deviation z = V/sqrt((V*)^2).
The possible corrections suggested by deviations of V from a normal
distribution become even less relevant at the end where several units are
combined to form one final z value.
In the units using random time intervals, where the independent observer
randomly selected one out of 10 numbers for the test score as opposed to
9 control scores, the question was whether the test scores were generally
larger than the control scores. Accordingly, the selected score was
compared with the other 9 scores in the same row. The selected score was
assigned a rank r when r of the scores in the row were lower
than the selected one. Thus, r can assume the integer values from
0 to 9. With the probability for ties negligible, the expectation value of
r is 4.5, and the variance of r is also known (we are dealing
with the statistics of a "ten-sided die"). The independent observer
evaluated the total significance in terms of the r values for all
rows of the printout. With expectation and variance of this sum known, a
z value could be easily calculated.
The Independent Observers
In all five experiments, there was another person (sometimes two others)
acting as independent observers who independently assigned the targets and
calculated the results. Some of these independent observers were psi
researchers, but we took careful formal precautions to guarantee that no
single person, independent observer, or experimenter could have simulated
high scores by fraud or human error.
The following list gives a brief description of the independent observers:
Experiment 1: Observers, Morris and Rudolph. Robert Morris presently
holds the Arthur Koestler
Chair for Parapsychology at the University of
Edinburgh. At the time of the experiment, he headed a psi research group
with the Department of Computer and Information Science at Syracuse
University. Luther Rudolph was a professor at the School of Computer and
Information Science at Syracuse University.
Experiment 2: Observer, Schlitz. Marilyn Schlitz holds a PhD in
Anthropology, and presently works in the Psychology Department at Stanford
University. At the time of the experiment, she was, like myself, a Research
Associate at the Mind Science Foundation. She has an active interest in
parapsychology and has published studies of her own.
Experiment 3: Observers, Morris and Hardin. Robert Morris (same as
above) holds the Arthur Koesder Chair for Parapsychology at the University of
Edinburgh. Larry Hardin was Professor of Philosophy at Syracuse University.
He had no particular interest in parapsychology.
Experiment 4: Observer, Braud. William Braud is now Director of
Research at the Institute of Transpersonal Psychology in Palo Alto. He was
a colleague of mine at the Mind Science Foundation, and has worked
extensively on PK effects acting on living systems (with their inherently
random features) rather than on electronic random number generators.
Experiment 5: Observer, Stapp. Henry Stapp is a theoretical
physicist at the Lawrence Berkeley Laboratory. His publications relate in
particular to elementary particle physics and the foundations of quantum
theory. He is interested in the role of consciousness in physics, but
maintains a sceptical outlook toward parapsychology.
Random Number Generation
The experimenter used a combination of a true random number generator and
a quasi-random algorithm to generate the primary random bit-sequences and
the random time intervals needed for the experiment.
The random generator utilized the timing of radioactive decay as the basic
source of randomness (Schmidt, 1970) to generate binary random bit-sequences.
Regular randomness checks never indicated any malfunctions of this device.
Nevertheless, as an additional precaution against the unlikely event of
generator malfunction, the resulting bit-sequence was combined through the
logical XOR operation with a cornputer-generated quasi-random bit-sequence,
based on the multiplicative algorithm R'= R*M (mod p) with
p = 2^19 - 1 = 524287, M = 242292. This procedure ensured
that even a complete breakdown of the "true random generator" could not
lead to a systematic bias in the final bit-sequence.
Random Target Assignments
The independent observers used a different random method to give target
assignments to the scores printed in the sealed lists.
The inclusion of the independent observers strengthened the reliability of
the experiment in two respects. First, even though the experimenter had
taken precautions to guarantee the desired randomness, the presence of one
more independent random source was an additional safeguard against
malfunctions on the part of the experimenter. Second, the arrangement
precluded fraud by the experimenter as well as fraud by the independent
observers.
In Experiment 1, the independent observers used their own random number
generator to determine the target assignments. Following a suggestion by
Robert Morris, the assignments in the subsequent experiments were derived
from future weather data. A prespecified number of days (for example, 7
days) after the independent observers received the sealed score printout,
they bought a prespecified newspaper (for example, The New York Times)
and derived from the last digit in a prespecified weather column a 6-digit
seed number. For Experiments 2 to 4, this seed number served as an entry
point into the RAND random number tables. The consecutive digits following
the entry point determined the binary target assignments (high/low for
even/odd digits), or the one of 10 scores in each line to be used as target
in the case of random intervals.
In Experiment 5, at his own suggestion, the independent observer used a
quasi-random algorid-im of his own choice rather than the RAND tables to
derive the target assignments from the weather data.
Protection Against Fraud
To preclude fraud by the experimenter, it was sufficient that (a) the target
assignments were determined after the experimenter had given the sealed score
printouts to the independent observers, and (b) the experimenter had no
further access to these records. In the two cases (Experiments 2 and 4)
when colleagues from the same laboratory acted as observers, the observers
kept the records securely in their homes rather than in the laboratory where
the experimenter might gain access to replace or alter the records.
To preclude fraud by the independent observers, the arrangement of the first
experiment called for two independent observers to watch each other. After
the experimenter sent the sealed printout to the home address of one
independent observer (Rudolph), the other independent observer (Morris)
used his own random generator to print out the sequence of target
assignments. Then the two independent observers met and exchanged copies
of their records. A copy of the target assignment list was then mailed to
the experimenter.
In Experiments 2 to 4, the target assignments, determined by future weather
data and by the RAND tables, were beyond anybody's control, and the proper
assignments calculated initially by the independent observers could later be
verified independently by the experimenter. There was no room for fraud
even with a single independent observer. Nevertheless, Experiment 3 used
two independent observers. Indeed, the arrangement can easily accommodate
any number of independent observers.
In Experiment 5, the situation was slightly different insofar as the single
independent observer used a quasi-random algorithm of his own choice to take
the place of the RAND tables. The experimenter did not know this algorithm
at the start. This would, in principle, have enabled the independent
observer to select an algorithm that would produce favorable scores. In
view of the rather skeptical attitude of this independent observer, however,
this possibility was considered to be negligible.
The Main Results
Table 2 lists the z values z(l),...,z(5) that determine the
significance levels obtained in the five experiments. All experiments gave
score deviations from chance in the desired direction, but the z
values for most experiments were too low to provide independent statistical
significance. Combining the results of all five experiments, however, we
obtain a total z value of
z(tot) = [z(l) + z(2) +...+ z(5) ] /sqrt(5) = 3.67.
The odds that the observed score or a higher total score could result from
chance are approximately 8,000 to 1.
Thus, the five experiments together provide convincing evidence for the
existence of an anomaly. (Detailed information on the individual experiments
and their units is provided in the Appendix.)
The reasons for compiling the results of the five experiments at this stage
are practical ones. First, such compilations seem appropriate at some
stages, and second, the author lost his financial support after the fifth
experiment, so that similar experiments might not be expected in the near
future.
TABLE 2
RESULTS OF THE FIVE EXPERIMENTS
| Experiment | z | Reference |
|---|
| 1 | 2.71 | Schmidt, Morris, and
Rudolph (1986) |
| 2 | 1.66 | Schmidt & Schlitz (1988) |
| 3 | 0.62 | Schmidt, Morris, & Hardin (1990) |
| 4 | 1.98 | Schmidt & Braud (1992) |
| 5 | 1.23 | Schmidt & Stapp (1993) |
Additional Questions Studied
Although the demonstration of the existence of PK under external supervision
was the main objective, additional questions were explored in some of the
experiments. In Experiment 2, for example, the performances of meditators
and nonmeditators were compared. The results suggested that meditators
performed better than nonmeditators. However, when only meditators were
used in Experiment 3, the total score was disappointing, so that even the
selection of meditators does not guarantee reliable performance.
Experiment 4 compared the PK action on prerecorded random events with PK
action on momentarily generated random events. For this purpose, each test
machine was equipped with an internal random number generator using
electronic noise as the basic source of randomness. During a test run, the
bits coming from this random generator were interlaced with prerecorded bits,
and that bit mixture was displayed so that the subject could not distinguish
between prerecorded and momentarily generated bits. The PK scores on the
two types of bits were internally recorded, but only at the conclusion of
the experiment were they inspected and evaluated. The result was surprising
in that it showed at least a suggestive difference between positive scoring
on the prerecorded events, (z = 1.98) and slight PK-missing (z
= - 0.23) in the momentarily generated events. It is interesting to note
that the experimenter was motivated to obtain high scores on the prerecorded
events, which were monitored by the independent observer. The outcome of
the directly generated events, which could not be monitored by the
independent observer, however, was of little concern to the experimenter.
We must leave the question open for the moment as to whether the observed
difference was a fluke of chance, an experimenter effect, or some other of
the "differential effects" that have puzzled researchers in the past.
Experiment 5 compared two kinds of binary events. For one kind, the
corresponding score was preinspected before the subject made the PK effort.
The two kinds of binary events were again interlaced so that the subject
could not distinguish between them. And also the experimenter learned the
possible scoring differences on the two kinds of events only at the end of
the whole experiment. The outcome of the experiment was a slightly positive
score on the not-inspected events (z = 1.23) and a slightly negative
score (z = - 0.93) on the preinspected events. At the start of the
experiment, it was considered as possible or even likely that preinspection
might inhibit the PK effects. Therefore, it was decided to use as evidence
for the existence of a PK effect only the results from the not-observed
events. Thus, the experimenter was motivated to obtain positive scores on
the not-inspected events, but was neutral toward the preinspected events.
With the difference between the two scores not statistically significant, we
have to wait for the outcome of further experiments.
CONCLUSION
Previous to this study, several independent researchers had reported the
existence of a PK effect. The present study confirms the existence of the
effect under particularly well-controlled conditions where the participation
of independent observers precludes experimenter error, or even fraud.
The PK effect appears as an anomalous correlation between the outcome of
random events and the mental state of a human subject observing the outcome.
The effect is only partly under voluntary control and may depend on
subconscious expectations, wishes, and fears of the observer.
Although the effect is usually weak, it may be of practical importance in
cases where conclusions have to be drawn from limited statistical evidence.
A physicist trying to confirm his own theory experimentally might
subconsciously generate a PK effect that could shift the outcome by, say,
two standard deviations in the desired direction. Similarly, the fear of
failure might induce PK effects opposite to the desired direction.
This could play a practical role in critical procedures such as the
launching of a satellite where, as we know from experience, elements of
chance cannot be completely excluded, and where even a small reduction of
the failure rate could be economically significant.
The most challenging aspect of PK is its incompatibility
with current
quantum theory. The experiments indicate that the outcome of quantum
jumps, which quantum theory attributes to nothing but chance, can be
influenced by a person's mental effort. This implies that current quantum
theory is wrong when experimentally applied to systems that include human
subjects. It remains to be seen whether the quantum formalism can be
modified to include psi effects, and perhaps even to clarify the still
somewhat puzzling role of the human observer in the theory.
The use of prerecorded events in the present study served two purposes.
First, it permitted the inclusion of independent observers, and, second, it
emphasized the difference between PK and the known physical mechanism.
Furthermore, the experiments raised a new question, the effect of
preinspection of the prerecorded data. The future study of this question
may shed new light on the psi mechanism and the role of consciousness.
APPENDIX
INFORMATION ON THE INDIVIDUAL UNITS
Table 3 provides details on the individual units, The unit labels in column 1
give the number of the experiment followed by the unit number within the
experiment. Each unit was divided into test runs, with a run lasting
typically between 15 and 60 sec. Column 2 gives the number of runs in the
unit and column 3 lists the approximate total test time in minutes.
Comparing the test times for the units provides an approximate measure of
the total time spent on the unit. In many cases, however, the subjects spent
considerable additional time in preparing themselves for the test runs. In
some cases (Experiment 2 and part of Experiment 3) the subjects received
feedback through mailed-out cassette tapes. In these cases the numbers of
tapes used, followed by a T, are given in column 2. Each tape held between
10 and 20 minutes of test time so that these units comprise a very large
total test time.
The number of participating subjects in column 4 varied from one to over a
hundred in some of the experiments with cassette tapes. The * next to the 1
in some units indicates that the author acted as the only subject. The
author also participated in some of the other units of Experiments 1 and 5,
mainly in an attempt to bring nearly completed units to an end.
The z values in column 5 were calculated independently by the
experimenter and by the independent observer using the previously described
procedures.
The different units used a large variety of feedback displays (column 6)
which were provided either by small test machines that could be mailed or,
in the case of mere auditory feedback, by cassette tapes. We will discuss
here only the main features of the displays and ignore minor variations.
The TV Pendulum Display used in parts of Experiments 1 and 3 was provided by
a small microprocessor system that the subjects could connect to their own
TV sets. The display showed a pendulum swinging on the screen, with the
amplitude randomly varying on a 7-step scale (random walk with two boundary
conditions). The subject had the choice (registered by the setting of a
switch) of aiming either for a high or a low average swing amplitude. The
task of increasing or decreasing a swing amplitude seemed psychologically
quite captivating so that a similar display was also used in Experiment 4
(31 Lamps) and part of Experiment 5 (27 Lamps, I). In these cases the TV
screen was replaced by a row of 31 or 27 lamps. With one lamp lighted at a
time, the light performed a swinging motion around the center lamp, with
randomly varying amplitudes. The PK goal was either to have the light swing
with maximal amplitude over the whole range, or to remain with minimal swing
amplitude near the center lamp. A frequently used variation was provided
by a mirror symmetric display where the subject saw two lights "bouncing
against each other" with randomly changing amplitudes.
An interesting auditory display (Clicks) was used in part of Experiment 1.
The subjects listened through stereo headphones to two different click
patterns. One pattern consisted of clicks sent simultaneously to both
headphones. This was perceived as clicks in the center of the head.
The other pattern consisted of clicks rapidly alternating between
the headphones. This was perceived as clicks coming from the outside.
TABLE 3
DATA ON THE INDIVIDUAL UNITS
| Unit | Runs | Test minutes | Number of Ss |
z | Display |
|---|
| 1/1 | 40 | 40 | 1* | 1.66 | TV
Pendulum |
| 1/2 | 40 | 40 | 2 | 0.39 | " |
| 1/3 | 40 | 40 | 2 | 0.49 | " |
| 1/4 | 40 | 40 | 2 | 0.20 | " |
| 1/5 | 120 | 120 | 2 | 1.71 | " |
| 1/6 | 120 | 30 | 1* | 1.13 | Clicks |
| 1/7 | 120 | 120 | 1 | 1.17 | TV
Pendulum |
| 1/8 | 120 | 120 | 1* | 0.89 | " |
| 1/9 | 240 | 240 | 6 | -0.17 | " |
| 1/10 | 160 | 40 | 1* | 1.18 | Clicks |
| 2/1 | 240T | 2400 | 240 | -1.20 |
Sound Tape |
| 2/2 | 140T | 2800 | 140 | 1.41 | " |
| 2/3 | 100T | 2000 | 100 | 1.53 | " |
| 2/4 | 100T | 2000 | 100 | 0.48 | " |
| 2/5 | 150T | 3000 | 150 | -0.26 | " |
| 2/6 | 50T | 1000 | 50 | -1.14 | " |
| 2/7 | 100T | 2000 | 100 | 1.36 | " |
| 2/8 | 100T | 2000 | 100 | 2.52 | " |
| 3/1 | 64 | 128 | 1 | 1.47 | TV
Pendulum |
| 3/2 | 96 | 192 | 1 | -0.76 | " |
| 3/3 | 96 | 192 | 1 | 0.23 | " |
| 3/4 | 80T | 1600 | 80 | 0.59 | Sound Tape |
| 3/5 | 40T | 800 | 40 | 0.16 | " |
| 3/6 | 40T | 800 | 40 | 0.15 | " |
| 3/7 | 80T | 1600 | 80 | 0.64 | " |
| 3/8 | 40T | 800 | 40 | -0.72 | " |
| 4/1 | 256 | 256 | 4 | 1.21 | 31 Lamps |
| 4/2 | 256 | 256 | 12 | 0.52 | " |
| 4/3 | 256 | 256 | 3 | 1.66 | " |
| 4/4 | 256 | 256 | 10 | -0.35 | " |
| 4/5 | 256 | 256 | 3 | 1.38 | " |
| 5/1 | 200 | 100 | 10 | 0.36 | 27 Lamps (II) |
| 5/2 | 200 | 100 | 9 | -0.24 | " (II) |
| 5/3 | 200 | 200 | 7 | 1.54 | " (I) |
| 5/4 | 200 | 200 | 4 | 1.34 | " (I) |
| 5/5 | 200 | 200 | 9 | 0.67 | " (I) |
| 5/6 | 200 | 100 | 6 | 1.91 | " (II) |
| 5/7 | 200 | 100 | 7 | 0.38 | " (II) |
| 5/8 | 200 | 200 | 8 | 0.27 | " (I) |
| 5/9 | 200 | 200 | 8 | -0.18 | " (I) |
| 5/10 | 200 | 200 | 12 | 0.64 | " (I) |
| 5/11 | 100 | 50 | 1 | -0.64 | " (II) |
| 5/12 | 100 | 50 | 1 | -1.37 | 27 Lamps (II) |
| 5/13 | 100 | 50 | 1* | 0.93 | " (II) |
| 5/14 | 100 | 50 | 2 | -1.22 | " (II) |
| 5/15 | 100 | 50 | 1 | 0.14 | " (II) |
| 5/16 | 100 | 100 | 1 | 0.83 | " (I) |
| 5/17 | 100 | 100 | 1 | 0.27 | " (I) |
| 5/18 | 100 | 100 | 1* | -0.61 | " (I) |
| 5/19 | 100 | 100 | 1 | 1.18 | " (I) |
| 5/20 | 100 | 100 | 1 | -0.69 | " (I) |
The display was driven by a binary sequence, with a 1 initiating the first
pattern and a 0 initiating the second pattern. This display is promising
for further work because the subject does not have to "reach out" in the
PK effort, but has to affect things that are perceived as happening "inside
the head."
A number of different sound displays provided by cassette tapes required
the subjects to move tones up or down on certain scales (random walk with
two boundaries), to extend the durations of tones, or to extend the duration
of pleasant and shorten the duration of unpleasant tones (random time
intervals).
In the cases discussed so far, the duration of a run was long enough
(generally .5 min or more) so that the feedback could affect the subject's
mental state, and with it possibly the scoring level.
In part of Experiment 5 (27 Lamps, II), the runs were very short, some only
a few seconds, so that the subject had no time to reflect on the performance
during the run, but, rather, approached the task with a "burst of energy"
gathered before the start. (I had hoped that this approach would work
particularly well with martial arts students, but the results were rather
disappointing.) A typical test run displayed an unrestricted 128-step random
walk of a light on a string of 27 lamps. The subjects tried to move the
light toward a specified side, and whenever the light reached the right or
left edge, it was automatically reset to the center to continue its random
walk.
For further details, such as the selection of subjects, the reader is
referred to the original reports.
REFERENCES
RADIN, D., and NELSON, R. (1989). Evidence for consciousness-related
anomalies in random physical systems. Foundations of Physics,
19, 1499-1514.
RHINE, L.E., and RHINE, J.B. (1943). The psychokinetic effect.
Journal of Parapsychology, 7, 20-43.
SCHMIDT, H. (1970). Quantum mechanical random number generator.
Journal of Applied Physics, 41, 462-468.
SCHMIDT, H. (1971, June). Mental influence on random events.
New Scientist and Science Journal, 757-758.
SCHMIDT, H. (1975). Toward a mathematical theory of psi.
Journal of the American Society for Psychical Research, 69,
301-319.
SCHMIDT, H. (1976). PK effect on prerecorded targets. Journal of the
American Society for Psychical Research, 70, 267-291.
SCHMIDT, H. (1978). Can an effect precede its cause?
Foundations of Physics, 8, 463-480.
SCHMIDT, H. (1981). PK effects with prerecorded and pre-inspected seed
numbers. Journal of Parapsychology, 45, 87-98.
SCHMIDT, H. (1982). Collapse of the state vector and psychokinetic effect.
Foundations of Physics, 12, 565-581.
SCHMIDT, H. (1984). Comparison of a teleological model with a quantum
collapse model of psi. Journal of Parapsychology, 48, 261-276.
SCHMIDT, H. (1985). Addition effect for PK on prerecorded targets.
Journal of Parapsychology, 49, 229-244.
SCHMIDT, H. (1987). The strange properties of psychokinesis.
Journal of Scientific Exploration, 1, 103-118.
SCHMIDT, H., and BRAUD, W. (1992). New PK tests with an outside observer.
Journal of Parapsychology, 57, 227-240.
SCHMIDT, H., MORRIS, R.L., and HARDIN, C.L. (1990, September). Channeling
evidence for a psychokinetic effect to independent observers. (Mind Science
Foundation Research Report.) San Antonio, TX: Mind Science Foundation.
(See also abstract in Research in Parapsychology 1991.)
SCHMIDT, H., MORRIS, R.L., and RUDOLPH, L. (1986). Channeling evidence for
a PK effect to independent observers. Journal of Parapsychology,
50, 1-15.
SCHMIDT, H., & SCHLITZ, M. (1988, December). A large-scale pilot PK
experiment with prerecorded random events. (Mind Science Foundation
Research Report.) San Antonio, TX: Mind Science Foundation. (See also
abstract in Research in Parapsychology 1991.)
SCHMIDT, H. and STAPP, H. (1993, June). Study of PK with prerecorded
random events and the effects of preobservation. Mind Science Foundation
Research Report. San Antonio, TX: Mind Science Foundation (See also
Journal of Parapsychology, current number.)
P.O. Box 296
Mora, NM 87732-0296



 RetroPsychoKinesis Project Home
RetroPsychoKinesis Project Home