CHANNELING EVIDENCE FOR A PK EFFECT TO INDEPENDENT OBSERVERS

BY H. SCHMIDT, R. MORRIS, and L. RUDOLPH

(Originally published in Journal of Parapsychology, Vol. 50, March 1986)

When L.E. and J.B. Rhine (1943) first reported a PK effect on the outcome of dice falls, PK appeared to be a kind of force comparable to the known physical forces. But with later research, the idea of PK became more abstract, less intuitively understandable. Furthermore, a close relationship between PK and ESP was suggested, and this led to the introduction of a common name, psi. If we label this study as being a PK experiment, this should not be a claim for any particular "mechanism"; it should only describe the experimental set-up, in which a subject mentally tried to obtain a specified result. What we actually observed and report is an "anomalous correlation" between apparently unrelated events.

In spite of many reported confirmations of the existence of psi effects, there has remained a credibility gap between the successful active researchers and the critical outsiders. A major reason for this is that a critic cannot easily obtain firsthand evidence of psi. A convincing documentation of the weak effects typically requires several months, so that firsthand observation by the critic seems impractical. The critic may convince himself of the adequacy of the test apparatus, but in the end he has to trust the reliability of the experimenter.

Ways to overcome these difficulties most easily and elegantly are suggested by PK experiments with prerecorded targets. In this study we use a variation of this method, PK tests with prerecorded random seed numbers, in an attempt to channel psi evidence from the laboratory of the experimenter (HS) in San Antonio to two independent observers (RM and LR) at Syracuse University. These independent observers were not critics of parapsychology in general, but they were rather critical toward the idea of channeling PK effects.

Our test arrangement was very convenient for subjects and observers. The subjects could work at home, and do so whenever they wanted. And the observers could, at the end, very easily confirm the evidence for psi.

PK experiments with prerecorded targets (Schmidt, 1976) emphasize the implausible features of psi. On the other hand, the ideas that lead to such experiments are not far-fetched.

In the absence of a good psi theory, it seems natural to search for general psi principles that might serve as building blocks for some future theory. Two interesting, often-discussed possibilities for such general principles are the equivalence hypothesis and the weak violation hypothesis:

The equivalence hypothesis. Briefly, the equivalence hypothesis (Schmidt, 1974) says that the PK success rate is independent of the random generator, provided that the psychological conditions are constant and the random decisions are based on truly random processes.

The weak violation hypothesis. The weak violation hypothesis, already implicitly suggested by Beloff and Evans (1961), implies that PK violates conventional physics only in a weak sense. Only the outcome of indeterministic quantum processes can be affected, whereas the nonstatistical laws, like the conservation laws for energy, momentum, symmetry, and so forth, remain in force. Therefore, PK can achieve nothing that is strictly forbidden by conventional physics. Only the probabilities for the outcomes of chance processes may change.

These two hypotheses so far seem in agreement with experiments, and their simple and universal character may appear attractive. We make no strong claims to the validity of the hypotheses. What matters most is that the hypotheses can stimulate interesting experiments.

It is easily seen how these two hypotheses lead to PK experiments with prerecorded targets and to the possibility of channeling psi evidence to independent observers. Consider, for example, the following arrangement (the slightly different set-up in our experiment will be explained later).

First, signals (1's and 0's) from a binary random generator are recorded simultaneously on two cassette tapes. Next, one of the identical tapes is given to an independent observer who, without looking at the recorded data, specifies the subject's PK aim, an excess of 1's or an excess of 0's. Finally, the sequence of 1's and 0's from the other tape is displayed to the PK subject, who is trying to mentally enforce the appearance of predominantly 1's or 0's, as specified by the independent observer.

In this example, the equivalence hypothesis suggests that the subject may still succeed in his PK effort, because PK should work equally well on all types of true random generators. The weak violation hypothesis, on the other hand, implies that the two tapes should still agree after the PK effort, because the identical recording of the two tapes was guaranteed by reliable recording equipment that leaves practically no room for chance (and with it PK effects) to enter.

Thus, the independent observer can, at the end, confirm the success of the PK effort firsthand, by playing his copy of the tape into a computer that counts the recorded 0's and 1's.

Previously reported experiments (Schmidt, 1976) (without independent observers) suggest that PK still operates under these conditions and that the two records still agree after the PK effort.

In an attempt to interpret these results (Schmidt, 1976, 1984), one might speculate that the PK mechanism is truly noncausal, that the subject's effort reached back to the time when the random events were generated (which would explain why the copies agree). As an alternative, one might try to avoid such noncausality by the argument that, perhaps, events are not physically real until there has been an observation. From this viewpoint, the PK effort would not have to reach into the past because nature had not yet decided on the outcome before the PK subject, the first observer, saw the result. Then, the PK effort should no longer succeed if we have some other observer look at the prerecorded data previous to the PK subject's attempt. The only experiment to study this situation so far has, indeed, reported a blocking of the PK effect by a previous observation (Schmidt, 1985).

A specific type of PK tests with prerecorded targets is provided by tests with prerecorded seed numbers (Schmidt, 1981). Let us discuss such a test arrangement, which will lead us directly into the study to be reported.

One can easily program a computer to do the following: After some "seed number" is entered, the computer uses a quasi-random algorithm to derive from the seed a quasi-random sequence of, say, one hundred 1's and 0's, which are individually displayed to the subject at a rate of one per second. Let us define the score of the run as the number of generated 1's. Then the entered seed number completely determines the resulting score. And if the seed number is chosen by a truly random process, then the score contains some truly random elements and might be subject to a PK effort. Previous tests (Schmidt, 1981) have indicated that PK effects still occur under these conditions and that the PK effect persists even if the seed numbers are seen by a human observer before the PK subject makes his effort. This may seem surprising in view of the previously mentioned experiment (Schmidt, 1985), in which preinspection of the binary events foiled the later PK effort. Note, however, that the observer of the seed number receives no practical knowledge with regard to the resulting score (Schmidt, 1982).

This kind of experiment lends itself easily to tight supervision by an independent observer. Consider for example the test procedure with the following steps:

At the end, if the PK effort has been successful, the seeds marked H show significantly higher scores than the seeds marked L. This, however, can be confirmed by the independent observer:

And if the subject has been successful, the independent observer finds the "inexplicable" result that the seeds he happened to mark H led to higher scores than the seeds marked L. Without having to trust anybody else, the independent observer can detect, firsthand, an anomalous correlation between his random assignments and the actual scores.

In the present study we used the outlined procedure with minor modifications. HS in San Antonio, Texas, was the experimenter. To give the reader maximal confidence in the results, we used two independent observers at Syracuse University, NY. This guaranteed that not any single one of us could have caused the appearance of high scores by negligence or fraud.

METHOD

Most of the tests were done with a small computer (RCA, with COSMAC microprocessor) programmed to do the following:

After a 6-digit seed number was entered, the computer used a shift register algorithm to derive a quasi-random sequence of 1's and 0's. This sequence, in turn, regulated the movement of a pendulum, which could swing on a TV screen with eight different amplitude values. After each half-cycle, the computer read the next random bit and, for a 1 or 0, respectively, increased or decreased (if possible) the amplitude by one step. After 128 half-cycles, the process stopped and a score proportional to the average pendulum amplitude during the run was displayed. Thus, a given seed number always led to the same score. The pendulum frequency could be chosen by the subject. Typical values ranged between 1 and 2 hertz, providing run durations from 1 to 1/2 minutes.

For each test run, in the normal mode of operation, the subject entered the next seed number, noted the associated target assignment, H or L, and then tried to enforce a high or low pendulum amplitude, respectively.

The observers had an identical computer so that they could later calculate the scores. The observers were also supplied with a BASIC program to calculate the scores from the seeds. This program is listed in Appendix 1.

For the subjects' convenience, a display inversion option was added. In the normal mode, high scores were associated with high pendulum amplitudes. But if, for example, the protocol asked for a high score but the subject preferred aiming at low-swing amplitudes, the subject could choose an inverted display mode where high scores were displayed by low amplitudes.

Another feature appreciated by the subjects was a provision for unrecorded practice runs. For these runs, the computer selected a random seed number, with the random element provided by the timing of the subject's key pushes.

The described arrangement, used in most tests, is labeled in Table 1 as SWING2. An earlier arrangement, SWING1, was similar but did not provide an inversion option. The program was somewhat more elaborate insofar as the pendulum motion was obtained by a superposition of three sine motions with equal, constant amplitudes but gradually randomly changing relative phases.

A third arrangement, CLICK, was different insofar as auditory rather than visual feedback was provided. The subject listened to two types of randomly alternating click patterns. One pattern, consisting of signals alternating between the ears, was felt to originate outside the head, whereas the other pattern, clicks administered to both ears simultaneously, gave the impression of clicks coming from the center of the head.

In the normal mode, high scores were associated with an increased number of center clicks, but an inversion option was available.

We decided in advance on the test procedure and the final statistical evaluation method described below. In particular, the whole experiment was to consist of 10 sections of test runs. Each section was to be evaluated independently, and the total significance was to be calculated from the resulting 10 scores.

As a first step, the experimenter used a computer with an attached Geiger counter arrangement to generate and to print a supply of truly random 6-digit seed numbers sufficient for the whole experiment. Some previous randomness tests with this arrangement had indicated no deviations from randomness. But we need not go into this because the later nonparametric evaluation method makes no assumptions about the randomness of the seed numbers.

At the start of each section, the experimenter decided on the number of test runs to be made in the section and on the test arrangement (SWING1, SWING2, or CLICK) to be used. Then the experimenter mailed a corresponding supply of seed numbers to the home address of the first observer (LR) and informed the second observer (RM) via telephone of the number of trials to be made and the test arrangement to be used. The second observer had already received either the corresponding computer or the computer program to calculate the scores for given seed numbers. (For the evaluation of the SWING experiments, the observers used the supplied computers, and for the CLICK tests, they used the BASIC program.)

Next, the second observer, who had at this stage no access to the seed numbers, used his own electronic random generator (with electronic noise as source of randomness) to generate and record a sequence of binary decisions to specify the target assignments. One decision (H or L) was recorded for each pair of subsequent seeds, specifying the target for the first seed, and the second seed in the pair got the opposite assignment.

Subsequently, RM and LR met to exchange copies of the seed number lists and the corresponding target assignment sequences. A copy of the seed number list and a copy of the generated target sequence were deposited with an administrative secretary of the School of Computer and Information Science at Syracuse University.

As the next step, HS phoned the secretary and received the target assignments to enter into his copies of the seed number lists.

Now the test sessions for this section of the experiment could begin. The subjects received a list of seed numbers with target assignments and the small test computer so that they could work at home at their convenience. The subjects were encouraged to complete not more than six test runs in one session and to begin tests only on days when they felt particularly well and confident. In addition, the subjects had the option to do informal practice runs before starting test runs.

When a section was completed, the experimenter informed the observers that they could now use their computer to calculate the scores for the seed numbers. From the run scores, the observers could derive a significance measure for the whole section. The corresponds ing calculations were also carried out independently by the experimenter.

Let us explain the details of the evaluation, taking the third section as an example. This section comprised 40 trials. The corresponding 6-digit seed numbers that had been generated and recorded by the experimenter at the start were the following:

These seed numbers were sent to the first observer. The second observer generated with his own random generator the following target assignments:

These assignments refer to the first member in successive pairs of seed numbers, the second member having the opposite assignment.

The observers had been informed at the start that this section was to use the SWING2 arrangement, and they had received a copy of the experimenter's computer to calculate the scores for the 40 seeds. The reader may make the corresponding calculation with the help of the BASIC listing in Appendix 1. The first two scores, for example, are: Score(735563) = 580, and Score(808629) = 332. From these scores we can derive for each trial-pair a pair-score:

Pair-score = [score of H-seed] - [score of L-seed]

The resulting 20 pair-scores are:
248, 80, 72, -236, 201, 368, 90, 336, 5, -64,
-113, 15, -188, 173, 41, -39, -278, -193, 140, -217

Under the chance hypothesis, positive and negative values in this sequence are equally likely. The subject's PK effort, however, was directed toward biasing these numbers toward positive values. To check for such a bias, a t test might seem appropriate. To avoid any assumptions about the distribution, however, we used a nonparametric rank order test (Hoel, 1962).

First we re-ordered the sequence according to absolute values. (In case of a tie, we maintained the original relative order, and if there were zero values, we omitted them.)

This led to the ordered sequence:
5, 15, -39, 41, -64, 72, 80, 90, -113, 140,
173, -188, -193, 201, -217, -236, 248, -278, 336, 368

Considering only the signs of the numbers, we define a new sequence E(s), with E(s)=1 or 0 for a positive or negative number, respectively. And we decide to measure a positive bias in terms of the random variable

W = [SUM s]sE(s).

The corresponding generating function is seen to be

F(x) = 2^N[SUM s]p(s)x^s = (1 + x)(1 + x^2)(1 + x^3)...(1 + x^N),

that is, p(s) is the probability for observing a particular value of W=s.

From Equation 2 we can easily derive the expectation value and the variance of W

W~ = N(N + I)/4.
sigma^2 = N(N + 1)(2N + 1)/24.

In our case, we have (with N=20):

W= 1 + 2 + 0 + 4 + 5... +0 + 19 + 20 = 119.
W~= 105; sigma = 26.8

Therefore, the observed W value is slightly, by z standard deviations, above chance expectancy, with

z = (W - W~)/sigma = 0.52 (without continuity correction.)

If the random variable W had a normal distribution, then the chance probability p for obtaining the observed or a higher W value by pure chance would be given by

p=(2*pi)^(-1/2)[Int z to inf] e^(-x^2/2)dx

With a computer, we can easily calculate the coefficients of the generating function and determine p exactly. This gives:

p = 0.31,

and if we use Equation 8 to calculate the associated z, we obtain the corrected value:

z = 0.49.

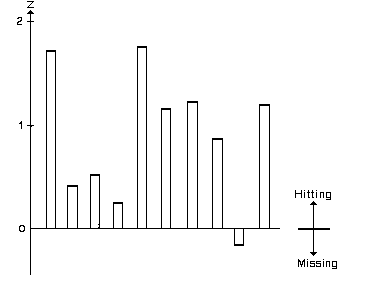
Table 1 lists these corrected z values for all 10 sections.

TABLE 1
RESULT OF THE 10 SECTIONS OF THE EXPERIMENT

Section	Program	Subjects	Trials	z
1	SWING1	HS	40	1.66
2	SWING1	HS, FG	40	0.39
3	SWING2	HS, FG	40	0.49
4	SWING2	FG, JN	40	0.20
5	SWING2	HS, DR	120	1.71
6	CLICK	HS	120	1.13
7	SWING2	GS	120	1.17
8	SWING2	HS	120	0.89
9	SWING2	6 S's	240	-0.17
10	CLICK	HS	160	1.18
Total			1,040	2.73

Note. The subjects were selected because of their promising scores in pilot tests. The experimenter (HS), in the role of a subject, contributed a considerable part of the results.
The programs SWING 1 and SWING2 provided feedback in the form of a pendulum swinging on a TV screen with randomly varying amplitude. The CLICK program gave auditory feedback by two types of clicks.
The z values measure the deviation of the scores from chance in the desired direction in units of one standard deviation.

RESULTS

At the end of the experiment, the observers and the experimenter had independently evaluated all sections in the manner described. Table 1 lists the obtained z values. These values are also plotted in Figure 1. It is seen that 9 of the 10 sections produced scores in the desired direction. To assess the significance of the whole experiment, we calculate a combined z value:

z = [z(1) + z(2) +. . .+ z(10)]/([sqrt]10) = 2.71.

Under the null hypothesis, the probability for obtaining such a high or a higher z value (as the result of chance) is

p = .0032 (odds against chance of 300:1).

At this level of statistical significance, the independent observers could confirm the existence of an anomalous correlation between their target assignments and the actual scores.

Figure 1. Result of the 10 sections of the experiment. The figure plots the z scores for the 10 sections. Positive values indicate scoring in the desired direction. Under the chance hypothesis, positive and negative z values are equally likely.

DISCUSSION

The reported study represents our first attempt to confirm previously reported PK results under full supervision by independent observers. We had decided in advance to submit the results for publication no matter what the outcome would be.

With its moderate statistical significance (odds against chance of 300:1), this experiment in itself may not dispel all of the critics' doubts about the reality of psychic phenomena. Considering, however, that the work provides a confirmation of earlier reported results, one might not want to dismiss the result lightly.

From the view of the independent observers, the result appeared as an "anomalous correlation," not understandable in terms of current physics. By labeling the effect as psychokinesis (PK), we do not want to imply any particular underlying mechanism. The term should only characterize the experimental set-up with a test subject who tried to mentally affect some form of display.

We make no claims about the validity of the theoretical speculations that led to the design of the experiment. One might even wonder whether the PK effect did not enter through the second observer, subconsciously forcing his random generator into producing favorable target assignments. Speaking against this mechanism are the previous experiments that obtained positive results without the participation of observers. But with no good theory available and the experimental results far outside the range of our everyday experience, one should view all plausibility arguments about underlying mechanisms with caution.

Copies of the original seed number lists with their target assignments are on record with the Journal of Parapsychology. They can be made available to readers who want to perform further analysis on the data.

APPENDIX I
QUASI-RANDOM ALGORITHMS

We need a quasi-random algorithm to derive two things from a given seed number: (a) a sequence of events to be displayed to the subject and (b) a corresponding final score. When the subject tries to affect the event history in a specified manner, the score should give a reasonable measure of the subject's success.

Three slightly different arrangements were used, labeled in Table 1 as SWINGI, SWING2, and CLICK.

The first two arrangements used the same algorithm for generating a binary quasi-random sequence, but the resulting bits had different effects on the display and on the final score.

With SWINGI, the pendulum coordinate was the sum of three sine waves with constant amplitudes but gradually changing relative phases. These phase changes were regulated by the quasi-random bit sequence, and the final score was proportional to the average pendulum amplitude in the run. This arrangement produced a particularly smooth and pleasing pendulum motion, but the relationship between the seed and the resulting score is too complex to be written out here explicitly. This was no problem for the observers. They had received at the start a copy of the test machine, where they simply had to enter the seed and wait for the final score to appear.

The arrangement SWING2 had a simplified display. The pendulum could swing only with eight discrete amplitudes. At each passage through the center, the next bit decided whether to increase or decrease (if possible) the amplitude by one step. For all practical purposes this simpler display seemed good enough. In this case, we can discuss the mathematics explicitly.

The heart of the quasi-random program is provided by a "shift register" with 31 bits, ....... B(31). The change of the bits in one shift operation is given by

B'(1) = B(28) XOR B(31)
B'(n) = B(n - 1) for n = 2, 3,... 31
XOR = Exclusive OR Operation.

Unless all bits vanish, the bit sequence returns to its original state only after P = 2^31 - l = 2,147,483,647 shifts, where P is a prime number.

Let us list a translation of the original machine language program into BASIC. When a 6-digit seed is entered, the program prints the resulting 128 amplitude values for the pendulum, as well as the final score, adjusted to an average value of 500.

The CLICK program provided feedback by "center clicks" and "side clicks," that is, clicks that were felt at the center of the head or on the sides (Schmidt,1985). The feedback for one test run was based on a sequence of 100 random integers in the range from 0 to 7. In the normal mode, the random numbers RN = 4, 5, 6, or 7 produced 1, 2, 3, or 4 center clicks, respectively. And the random numbers RN = 1, 2, 3, 4 produced 4, 3, 2, or 1 side clicks. Thus, aiming for many center clicks but few side clicks was equivalent to aiming for high random numbers. Accordingly, the score was defined as the sum of the 100 generated random numbers.

The program, running on a Z80 microprocessor, used a linear congruential algorithm to generate a quasi-random sequence R(n), with

R(n+1) = M * R(n) [modulo P].
P = 2^19 - 1 = 524287.
M = 242293.

The number P is a prime and M is a primitive root (Hardy & Wright, 1945) of the equation

x^(P-1) = 1 [modulo P]

Then, for any 6-digit seed number R(0), different from 0 and P, the quasi-random number sequence has maximal cycle length, that is, the numbers R(0), ....... R(P- 1) are all different.

After a preshuffle, the program uses only the three most significant bits of 100 consecutive random numbers to obtain a sequence of random integers in the range from 0 to 7.

The following BASIC program lists this sequence and prints the final score.

REFERENCES

RetroPsychoKinesis Project Home