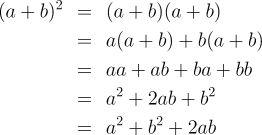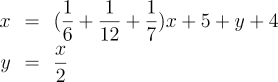- Mazur, Joseph.
Enlightening Symbols.
Princeton: Princeton University Press, 2014.
ISBN 978-0-691-15463-3.
-
Sometimes an invention is so profound and significant yet apparently
obvious in retrospect that it is difficult to imagine how people
around the world struggled over millennia to discover it, and how
slowly it was to diffuse from its points of origin into general use.
Such is the case for our modern decimal system of positional
notation for numbers and the notation for algebra and other
fields of mathematics which permits rapid calculation and
transformation of expressions. This book, written with the extensive source citations
of a scholarly work yet accessible to any reader familiar with
arithmetic and basic algebra, traces the often murky origins of
this essential part of our intellectual heritage.
From prehistoric times humans have had the need to count things,
for example, the number of sheep in a field. This could be
done by establishing a one-to-one correspondence between the
sheep and something else more portable such as
one's fingers (for a small flock), or pebbles kept in a sack.
To determine whether a sheep was missing, just remove a
pebble for each sheep and if any remained in the sack,
that indicates how many are absent. At a slightly more abstract
level, one could make tally marks on a piece of bark or clay
tablet, one for each sheep. But all of this does not imply
number as an abstraction independent of individual items of
some kind or another. Ancestral humans don't seem to have
required more than the simplest notion of numbers: until the
middle of the 20th century several tribes of Australian
aborigines had no words for numbers in their languages at all,
but counted things by making marks in the sand. Anthropologists
discovered tribes in remote areas of the Americas, Pacific
Islands, and Australia whose languages had no words for numbers
greater than four.
With the emergence of settled human populations and the
increasingly complex interactions of trade between villages
and eventually cities, a more sophisticated notion of numbers
was required. A merchant might need to compute how many
kinds of one good to exchange for another and to keep records
of his inventory of various items. The earliest known
written records of numerical writing are Sumerian cuneiform clay
tablets dating from around 3400 B.C.
These tablets show number symbols formed from two distinct
kinds of marks pressed into wet clay with a stylus. While
the smaller numbers seem clearly evolved from tally marks,
larger numbers are formed by complicated combinations of the
two symbols representing numbers from 1 to 59. Larger numbers
were written as groups of powers of 60 separated by spaces.
This was the first known instance of a positional number system,
but there is no evidence it was used for complicated calculations—just
as a means of recording quantities.
Ancient civilisations: Egypt, Hebrew, Greece, China, Rome, and the
Aztecs and Mayas in the Western Hemisphere all invented
ways of writing numbers, some sophisticated and capable of
representing large quantities. Many of these systems were
additive: they used symbols, sometimes derived from
letters in their alphabets, and composed numbers by writing
symbols which summed to the total. To write the number 563,
a Greek would write
“φξγ”,
where φ=500,
ξ=60, and
γ=3. By convention, numbers were
written with letters in descending order of the value they
represented, but the system was not positional. This made
the system clumsy for representing large numbers, reusing
letters with accent marks to represent thousands and an
entirely different convention for ten thousands.
How did such advanced civilisations get along using number systems
in which it is almost impossible to compute? Just imagine a
Roman faced with multiplying MDXLIX by XLVII
(1549 × 47)—where do you start?
You don't: all of these civilisations used some form of
mechanical computational aid: an abacus, counting rods, stones
in grooves, and so on to actually manipulate numbers. The
Sun
Zi Suan Jing, dating from fifth century China, provides
instructions (algorithms) for multiplication, division, and
square and cube root extraction using bamboo counting sticks
(or written symbols representing them). The result of the
computation was then written using the numerals of the language.
The written language was thus a way to represent numbers, but
not compute with them.
Many of the various forms of numbers and especially computational
tools such as the abacus came ever-so-close to stumbling on the
place value system, but it was in India, probably before the
third century B.C. that a positional
decimal number system including zero as a place holder, with
digit forms recognisably ancestral to those we use today
emerged. This was a breakthrough in two regards. Now, by
memorising tables of addition, subtraction, multiplication,
and division and simple algorithms once learned by schoolchildren
before calculators supplanted that part of their brains, it was
possible to directly compute from written numbers. (Despite
this, the abacus remained in common use.) But, more profoundly,
this was a universal representation of whole numbers.
Earlier number systems (with the possible exception of that
invented by Archimedes in
The Sand Reckoner
[but never used practically]) either had a limit on the largest number
they could represent or required cumbersome and/or lengthy conventions
for large numbers. The Indian number system needed only ten symbols
to represent any non-negative number, and only the single
convention that each digit in a number represented how many of that
power of ten depending on its position.
Knowledge diffused slowly in antiquity, and despite India being on
active trade routes, it was not until the 13th century
A.D. that
Fibonacci
introduced the new number system, which had been transmitted
via Islamic scholars writing in Arabic, to Europe in
his
Liber
Abaci. This book not only introduced the new number
system, it provided instructions for a variety of practical
computations and applications to higher mathematics. As revolutionary
as this book was, in an era of hand-copied manuscripts, its
influence spread very slowly, and it was not until the
16th century that the new numbers became almost universally used.
The author describes this protracted process, about which a great deal
of controversy remains to the present day.
Just as the decimal positional number system was becoming established
in Europe, another revolution in notation began which would
transform mathematics, how it was done, and our understanding of
the meaning of numbers. Algebra, as we now understand it, was known
in antiquity, but it was expressed in a rhetorical way—in words.
For example, proposition 7 of book 2 of Euclid's Elements
states:
If a straight line be cut at random, the square of the whole
is equal to the squares on the segments and twice the
rectangle contained by the segments.
Now, given such a problem, Euclid or any of those following in
his tradition would draw a diagram and proceed to prove from
the axioms of plane geometry the correctness of the statement.
But it isn't obvious how to apply this identity to other
problems, or how it illustrates the behaviour of general
numbers. Today, we'd express the problem and proceed as
follows:
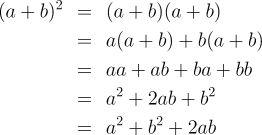
Once again, faced with the word problem, it's difficult to know where to begin,
but once expressed in symbolic form, it can be solved by applying rules of
algebra which many master before reaching high school. Indeed, the process of
simplifying such an equation is so mechanical that computer tools are readily
available to do so.
Or consider the following brain-twister posed in the 7th century
A.D. about the Greek mathematician
and father of algebra
Diophantus:
how many years did he live?
“Here lies Diophantus,” the wonder behold.
Through art algebraic, the stone tells how old;
“God gave him his boyhood one-sixth of his life,
One twelfth more as youth while whiskers grew rife;
And then one-seventh ere marriage begun;
In five years there came a bounding new son.
Alas, the dear child of master and sage
After attaining half the measure of his father's life
chill fate took him.
After consoling his fate by the science of numbers for
four years, he ended his life.”
Oh, go ahead, give it a try before reading on!
Today, we'd read through the problem and write a system of two
simultaneous equations, where x is the age of Diophantus
at his death and y the number of years his son lived.
Then:
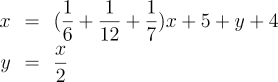
Plug the second equation into the first, do a little algebraic symbol
twiddling, and the answer, 84, pops right out. Note that not only are
the rules for solving this equation the same as for any other, with a
little practice it is easy to read the word problem and write down the
equations ready to solve. Go back and re-read the original problem and
the equations and you'll see how straightforwardly they follow.
Once you have transformed a mass of words into symbols, they invite you
to discover new ways in which they apply. What is the solution of the
equation x+4=0? In antiquity many would have said the
equation is meaningless: there is no number you can add to four to
get zero. But that's because their conception of number was too
limited: negative numbers such as −4 are completely valid and
obey all the laws of algebra. By admitting them, we discovered
we'd overlooked half of the real numbers. What about the solution
to the equation x² + 4 = 0? This was again considered
ill-formed, or imaginary, since the square of any real number, positive
or negative, is positive. Another leap of imagination, admitting the
square root of minus one to the family of numbers, expanded the
number line into the
complex plane,
yielding the answer 2i as
we'd now express it, and extending our concept of number into one which
is now fundamental not only in abstract mathematics but also science and
engineering. And in recognising negative and complex numbers, we'd
come closer to unifying algebra and geometry by bringing rotation
into the family of numbers.
This book explores the groping over centuries toward a symbolic
representation of mathematics which hid the specifics while revealing
the commonality underlying them. As one who learned mathematics
during the height of the “new math” craze, I can't recall
a time when I didn't think of mathematics as a game of symbolic
transformation of expressions which may or may not have any
connection with the real world. But what one discovers in reading
this book is that while this is a concept very easy to brainwash
into a 7th grader, it was extraordinarily difficult for even some
of the most brilliant humans ever to have lived to grasp in the
first place. When Newton invented calculus, for example, he always
expressed his “fluxions” as derivatives of time, and
did not write of the general derivative of a function of arbitrary variables.
Also, notation is important. Writing something in a more expressive
and easily manipulated way can reveal new insights about it. We benefit
not just from the discoveries of those in the past, but from those who
created the symbolic language in which we now express them.
This book is a treasure chest of information about how the language of
science came to be. We encounter a host of characters along the way,
not just great mathematicians and scientists, but scoundrels, master
forgers, chauvinists, those who preserved precious manuscripts and those
who burned them, all leading to the symbolic language
in which we so effortlessly write and do mathematics today.
January 2015