- Clawson, Calvin C. Mathematical Mysteries. New York: Perseus Books, 1996. ISBN 978-0-7382-0259-4.
-
This book might be more accurately titled “Wonders of Number
Theory”, but doubtless the publisher feared that would scare
away the few remaining customers who weren't intimidated by the
many equations in the text. Within that limited scope, and for
readers familiar with high school algebra (elementary calculus
makes a couple of appearances, but you'll miss little or nothing
if you aren't acquainted with it), this is an introduction to
the beauty of mathematics, its amazing and unexpected
interconnectedness, and the profound intellectual challenge of
problems, some posed in ancient Greece, which can easily be explained
to a child, yet which remain unsolved after millennia of effort by
the most intelligent exemplars of our species.
The hesitant reader is eased into the topic through a variety
of easily-comprehended and yet startling results, expanding
the concept of number from the natural numbers to the real number
line (like calculus, complex numbers only poke their nose under
the tent in a few circumstances where they absolutely can't be
avoided), and then the author provides a survey of the most
profound and intractable puzzles of number theory including
the
Goldbach conjecture
and
Riemann hypothesis,
concluding with a sketch of
Gödel's incompleteness theorems
and what it all means.
Two chapters are devoted to the life and work of
Ramanujan,
using his notebooks to illustrate the beauty of an
equation expressing a deep truth and the interconnections
in mathematics this singular genius perceived, such as:
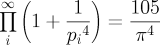
which relates the sequence of prime numbers (pi is the ith prime number) to the ratio of the circumference to the diameter of a circle. Who could have imagined they had anything to do with one another? And how did 105 get into it?
This book is a pure joy, and a excellent introduction for those who “don't get it” of how mathematics can become a consuming passion for those who do. The only low spot in the book is chapter 9, which discusses the application of large prime numbers to cryptography. While this was much in the news during the crypto wars when the book was published in the mid-1990s, some of the information in this chapter is factually incorrect and misleading, and the attempt at a popular description of the RSA algorithm will probably leave many who actually understand its details scratching their heads. So skip this chapter. I bought this book shortly after it was published, and it sat on my shelf for a decade and a half until I picked it up and started reading it. I finished it in three days, enjoying it immensely, and I was already familiar with most of the material covered here. For those who are encountering it for the first time, this may be a door into a palace of intellectual pleasures they previously thought to be forbidding, dry, and inaccessible to them.