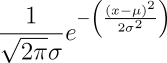
The probability of a result x in an experiment consisting of a large number of equally probable independent trials n is approximated by the normal probability density function:
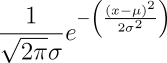
where μ, the mean value, is n/2 and σ, the standard deviation, is a measure of the breadth of the curve which, for experiments with two equally probable outcomes of each trial is:
Since the mean value and standard deviation depend upon the number of trials in the experiment, comparison between experiments with differing numbers of trials is facilitated by standardising the result: transforming it to a distribution with mean value zero and standard deviation of 1. A normally distributed experimental result x is thus standardised by subtracting the mean and dividing by the standard deviation of the experiment:
This z-value or z score expresses the divergence of the experimental result x from the most probable result μ as a number of standard deviations σ The larger the value of z, the less probable the experimental result is due to chance. The probability can be calculated from the cumulative standard normal distribution:
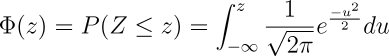
Which gives the probability P that an experimental result with a z value less than or equal to that observed is due to chance. Subtracting P from one:
gives Q, the probability that the observed z score is due to chance.
Unfortunately, there is no closed form solution for P, so it must be evaluated numerically. This page allows you to calculate the probability of chance occurrence of a given z, or to calculate z given a probability Q. All calculations are performed with six decimal places of accuracy; the maximum z accepted is 6.
Note that the probability calculated from the z is an approximation which is valid only for large values of n, and is therefore only meaningful when calculated for experiments with a large number of individual trials.
In order to use this page, your browser must support JavaScript. The text field below indicates whether JavaScript is available; if not, consider switching to a browser which implements it.
One of the most common probability calculations is determining, given the measured z value from an experiment or set of experiments, the probability of the result being due to chance. Enter the z value in the box below, press the Return key or the Calculate button, and the probability will appear in the Q box.
To determine the z score indicating a probability Q of non-chance occurrence for an experiment, enter Q in the box below and press the Return key or the Calculate button.
 RetroPsychoKinesis Project Home
RetroPsychoKinesis Project Home