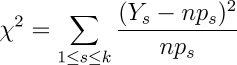
The chi-square statistic for an experiment with k possible outcomes, performed n times, in which Y1, Y2,… Yk are the number of experiments which resulted in each possible outcome, with probabilities of each outcome p1, p2,… pk is:
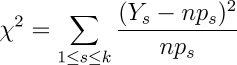
X² will be larger to the extent that the observed results diverge from those expected by chance. The probability Q that a X² value calculated for an experiment with d degrees of freedom (where d=k−1, one less the number of possible outcomes) is due to chance is:
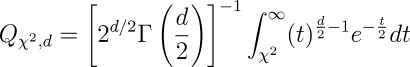
Where Γ is the generalisation of the factorial function to real and complex arguments:
![]()
Unfortunately, there is no closed form solution for Q, so it must be evaluated numerically. This page allows you to calculate the probability of chance occurrence of a given X² for an experiment with d degrees of freedom, or to calculate X² given d and the probability Q. All calculations are performed with six decimal places of accuracy; the maximum X² accepted is thus 99999.
Note that the probability calculated from the X² is an approximation which is valid only for large values of n, and is therefore only meaningful when calculated from a large number of independent experiments.
In order to use this page, your browser must support JavaScript. The text field below indicates whether JavaScript is available; if not, consider switching to a browser which implements it.
One of the most common chi-square calculations is determining, given the measured X² value for a set of experiments with a degree of freedom d, the probability of the result being due to chance. Enter the X² and d values in the boxes below, press the Calculate button, and the probability will appear in the Q box.
To determine the chi-square value indicating a probability Q of non-chance occurrence for an experiment with d degrees of freedom, enter Q and d in the boxes below and press Calculate.
 RetroPsychoKinesis Project Home
RetroPsychoKinesis Project Home