Rocket Science

by John Walker

“Rocket science” has often been used as a metaphor for something complicated, arcane, or difficult. Well, as one who has from time to time been called complicated, arcane, and difficult myself, I’m going to try to explain the essentials of it to you in this brief essay. There will be some math, but nothing you can’t do on a spreadsheet, pocket calculator, or slide rule.

First, let me distinguish rocket science, the physics which underlies rocket propulsion, which is relatively simple, from rocket engineering, which encompasses disciplines including propellant chemistry, thermodynamics, structural and vibration analysis, aerodynamics, guidance and control theory, fluid dynamics, and metallurgy. Rocket engineering is genuinely difficult, and is made even more challenging since most rockets are not reusable and hence, when you push the launch button, you’re trying out everything in a real flight for the first time.

At the level of the basic science, however, a rocket is pretty simple. You have a structure, usually tubular in shape, which holds some kind of propellant. In a chemical rocket, the propellant(s) burn, producing hot gases which issue from a nozzle at one end of the tube. The ejection of these gases creates, under Newton’s third law of motion, a reaction force upon the rocket, causing it to accelerate. How much acceleration do we get by burning all the propellant in a rocket? That’s given by the rocket equation, which Konstantin Tsiolkovsky applied in the late 19th century in his investigations of the feasibility of space flight. Don’t be afraid: it’s pretty straightforward once you get past the notation. Let’s look it in the face.

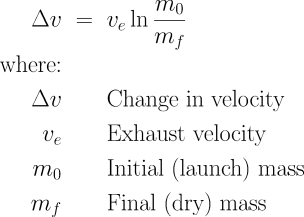
Δv (pronounced delta-vee) is the change in velocity which will result from burning all of the propellant in the rocket. This will have units like metres/second (m/s). The velocity of the exhaust which comes out of the rocket is v_e in the same units. The total mass of the rocket, including propellant, at the time of launch is m₀. The mass of the rocket (structure, payload, engine(s), avionics, etc.) which remains after all the fuel is burned is m_f. (This is sometimes called the “dry mass”, although that doesn’t really make sense in the case of solid rockets.) You can specify m₀ and m_f in any mass units (kilograms, tonnes, etc.) as long as they are the same: only the ratio matters. The natural logarithm function is ln. The key thing you need to know about the ln function is that it grows very slowly as its argument increases. This, as we’ll see, is what makes rocketry so difficult.

You’ll often hear the performance of rocket engines and propellants specified in terms of specific impulse, or I_sp. For rockets (as opposed to, say, air-breathing engines), this is simply another way of expressing the exhaust velocity, obtained by dividing the exhaust velocity by the gravitational acceleration at the Earth’s surface. If you have exhaust velocity in metres per second, you obtain I_sp in units of seconds by dividing by the acceleration of gravity of 9.8 m/s².

One advantage of using I_sp is that it’s the same regardless of which unit you use for length.

Let’s put some numbers on this to see the magnitude of what we’re talking about. Here are the exhaust velocities produced by some commonly used rocket propellants in modern, high-performance engines.

LOX is liquid oxygen; LH₂ is liquid hydrogen. Both are gases which must be liquefied and stored at cryogenic temperatures. Liquid hydrogen must be kept even colder than LOX and, because its density is low, requires large fuel tanks. RP-1 is essentially kerosene, and requires no special handling beyond that of diesel fuel or home heating oil. Nitrogen tetroxide (N₂O₄) and hydrazine (N₂H₄) are liquids at room temperature and can be stored indefinitely, ready to use. They are hypergolic with one another: they burst into combustion spontaneously on contact, so when used in rocket engines, no igniter is required; this makes them attractive for engines which must restart multiple times. Unfortunately, both nitrogen tetroxide and hydrazine are highly toxic and must be handled with extreme caution. A wide variety of solid rocket propellants are used. They have both fuel and oxidiser mixed together, and require only an igniter to set them burning. Obviously, great care must be taken that they aren’t ignited prematurely, and once lit, they burn to completion whether you like it or not. The one I’ve cited here is ammonium perchlorate composite propellant (APCP). Other widely used solid propellants are HTPB and PBAN (follow the links for their jaw-breaking names).

All right, enough with the equations, numbers, and acronyms. Let’s go fly a rocket and see how all this stuff actually works. We’ll begin with a very simple rocket, the GEM-60 solid rocket booster optionally used by the Delta IV launch vehicles. While it is normally used as a booster in the early part of a launch and then jettisoned, here we’re going to launch it by itself, just to see what happens. We will have no payload: just the rocket itself. Fully packed with propellant, the GEM-60 weighs 33,638 kg (m₀). At burn-out, just 91 seconds later, the final mass (m_f) is but 3,941 kg. Exhaust velocity (v_e) from the HTPB solid fuel is 2401 m/s, for an I_sp of 245 s. Plugging these numbers into the rocket equation, we find Δv to be 5148 m/s. Now, the rocket equation is for an ideal rocket, operating perfectly efficiently in a vacuum without the effects of air resistance or gravity, but let’s just go with that number for the moment. This is pretty fast; in fact, “faster than a speeding bullet” doesn’t do justice to it. The 5.56×45 NATO round fired by the M-16 rifle has a muzzle velocity of 940 m/s, so our rocket will not just be faster than the bullet, but more than five times faster. Pretty impressive, but what if we want to go to orbit?

Forget about it! Orbital velocity in low Earth orbit is around 7.8 km/s, but when you take into account the effects of gravity and air resistance during the first part of the rocket’s flight through the thick atmosphere, you’ll need around 9.5 km/s of Δv to get to orbit if you’re launching toward the East reasonably close to the equator, more otherwise. (When launching to the East, you get to add the Earth’s rotation to your Δv for free.) Now, you might think, from the simple rocket we’ve just worked out, “Well, we’re half way there. How hard can it be?” And now we come back to that natural logarithm function in the rocket equation; it’s a killer. With a little algebra we can rewrite the equation as:

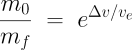
The quantity on the left is called the mass ratio: the ratio of the mass of the rocket at launch to the mass at burnout. Now you can see that this ratio increases exponentially as the ratio of Δv to exhaust velocity grows. The mass ratio of our simple rocket was 33638/3941=8.5. In other words, just 12% of the rocket’s weight at liftoff remained at burnout: at launch the rocket was 88% propellant. All right, let’s crank the numbers for an orbital launch, which requires a Δv of 9500 m/s. Now watch that exponential kick in! We get a mass ratio of, not 8.5, but 52! To reach orbit, our rocket would have to be 98% propellant on the launch pad. If we wanted to put one tonne (1000 kg) in orbit (including the rocket in the payload), we’d need the rocket to mass 52 tonnes on the launch pad. Not only is this ridiculously inefficient, we simply lack the materials to build structures this light compared to the weight they support.

What if we used a more energetic fuel? In the Golden Age of science fiction, many stories featured the discovery of a super-powerful rocket fuel which would open up the space frontier, and intrigue and derring-do involving access to the fuel. Experience has taught that unless you want to work with stuff so hideously toxic, volatile, expensive, and recalcitrant that nobody in their right mind would consider it, liquid oxygen and liquid hydrogen are the best you can do when it comes to chemical propellants. They are efficient, non-toxic, reasonably inexpensive, and their combustion product is just water vapour. Let’s try a LOX/LH₂ rocket and see how far we get. We’ll start with the first stage of the Delta IV launcher, which burns those propellants. This stage hasn’t ever been launched by itself, so we’ll add 500 kg for a nose cone, guidance system, and avionics with which it isn’t usually equipped. The stage, fully fuelled, has a mass of 228,400 kg and empty, 26,400 kg. Its energetic fuel delivers an exhaust velocity of 4057 m/s, or an I_sp of 414. Recall that exhaust velocity is in the denominator of that ratio in the exponential: this is an enormous improvement over the solid fuel booster! Our mass fraction, 8.7, is about the same, but the energetic fuel gives us a Δv of 8678 m/s. Much better, but we’re still short of the 9500 or so we need to get to orbit, and we’re still not carrying any payload.

We’re already using the highest energy fuel that’s practical, and burning it in a modern, high-performance rocket engine. The rocket structure is so light it allows 88% of the liftoff weight to be fuel. What is to be done? If only we could launch our rocket at a higher altitude, with a kick to get it started, rather than having to make it crawl all the way up from the ground through the dense lower atmosphere, losing Δv to the drag of gravity! Well, that’s exactly what we’ll do.

From the early days of rocketry, engineers who worked out the consequences of the rocket equation realised it was extraordinarily difficult to get to orbit from Earth’s surface. But, being engineers, they immediately asked themselves, “Can we cheat?” It turns out, you can. The trick is to use a large rocket to launch, as its payload, a smaller rocket. When the big rocket burns out, the smaller rocket is ignited, except now it’s not being launched from Earth, but rather with a high altitude and velocity, where its engine will operate more efficiently and have to provide less than the total Δv to get to orbit. This idea was demonstrated at the end of the 1940s by the RTV-G-4 Bumper program, which used a German V-2 to launch an American WAC Corporal rocket, which ultimately reached an altitude of 393 km. The Bumper launch pictured at the left was the first rocket launch from Cape Canaveral.

Now we’re going to get real. Let’s put some serious payload in low Earth orbit. We’ll start with the first stage of the Delta IV we used in the last example, but use it to launch a second stage: another rocket, which carries the actual payload. The properties and performance of the first stage are identical to those above. The second stage, which is called the Delta Cryogenic Second Stage (CSS), has a launch mass of 30,710 kg and a mass at burnout of 3490 kg. It is also fueled with LOX/LH₂, but since its engine only operates in a vacuum, is more efficient, with an exhaust velocity of 4628 m/s, or an I_sp of 462 s. On top of the second stage, we’ll stack a payload of 8000 kg (including a fairing we’ll dispose of after getting out of the atmosphere, but we’re doing science, not engineering here, so let’s neglect those details).

Three—two—one—zero—ignition—liftoff! The stack (first stage, second stage, and payload) lumbers off the launch pad. The numbers for the first stage are the same, but we must add the mass of the second stage and payload, which are (30710+8000)=38710 kg. As expected, this reduces Δv for the first stage, to 5092 m/s. But the second stage starts its work at this sweet spot, made even sweeter because it’s now outside the sensible atmosphere and runs more efficiently. To the mass of the second stage, we add the payload of 8000 kg. When the second stage burns out, it has contributed a Δv of 4451 m/sec, for a total for the two stages of 9543 m/s. We’ve delivered our payload to orbit.

Consider how difficult this was to do. The payload, 8 tonnes, is now in orbit. The total mass of the launcher was 267 tonnes less than ten minutes before. Only 3% of the mass of the launcher remains when the payload separates from the second stage; all the rest is junk. Even without considering the innumerable engineering details needed to accomplish such a mission, getting to orbit is hard. If the Earth were only slightly more massive than it is, it would be impossible to get to orbit using chemical propellants. Perhaps when we encounter other spacefaring species, most will hail from smaller planets, around the more numerous red dwarf stars. They’d be of slight stature, and have large eyes adapted to the dimmer light of their stars. But I’m not going there.

Rocket science can be fun, and it isn’t complicated. All you need to work out “what if” scenarios is a spreadsheet or pocket calculator, and abundant information available in the public domain on the Internet.

Here are the fundamentals of rocket propulsion explained in 1950 by that eminent rocket scientist, Prof. Woody Woodpecker, from Destination Moon.

This is a TEDxHouston talk by astronaut Donald Pettit about the tyranny of the rocket equation.

Scott Manley demonstrates rocket science with Kerbal Space Program and a spreadsheet.

This document is in the public domain.

Astronomy and Space at Fourmilab

Physics at Fourmilab

Fourmilab Home Page