
by John Walker

Before computers and calculators, there were slide rules. It is difficult for people today to appreciate just how magic it was to be able to carry a small tool, made of bamboo and plastic, that could perform many of the computations of engineering and science which used to be so tedious in mere seconds, as long as you were happy with its limited precision.
In my own years in engineering school, I did almost all of my homework and examination calculations with a slide rule and, when I graduated and was able to buy one of the first generation of pocket calculators (an HP-45), was amazed by its precision and ease of use, but had to admit that in practical work I could get the job done just about as fast with a slide rule.
The mathematical magic behind the slide rule is logarithms. Logarithms, invented in the 17th century, allow reducing multiplication to addition and division to subtraction. It is very easy to add and subtract by sliding two rulers against one another, so if you use rules whose scales are logarithmic instead of linear, you can multiply and divide without all of the tedious calculation, as long as you're satisfied with the accuracy you can read off the scale. With even more cleverly defined scales, it is possible to compute the squares of numbers, square roots, cubes and cube roots, trigonometric functions, and logarithms and exponents.
A slide rule does not add or subtract. Humans add and subtract, and with a little practice they get very good at it. (There is a famous scene in the film Apollo 13 where engineers start fiddling with their slide rules to add and subtract numbers. You can identify the balding engineers of my generation as those who chuckle in the theatre when this happens.) A slide rule also doesn't keep track of decimal places. It works only with the significant digits of numbers, and it's up to you to figure out where the decimal point goes in the result. This sounds tedious, and in the examples that follow it may seem so, but in fact users of slide rules could usually place the decimal by instinct, and if you got it wrong the result was usually so ridiculous you could go back and figure out where you'd goofed.
A slide rule is only as accurate as its manufacture and calibration and your ability to set it and read values. In practice, you get between two and three significant figures from slide rule calculations, and these errors compound as you use intermediate values in subsequent calculations. This may seem crude in an era where effortless 15-digit double precision arithmetic is at everybody's fingertips, but the fact is that it's all you need for many calculations in science and engineering. To a large extent (apart from trajectory calculation and mission planning), it got us to the Moon.
Let's start with a very simple calculation.
You have a truck which can haul a maximum load of 1000 kg (1 tonne). You're asked to haul a load of 35 sacks of turnips which weigh 28 kg each. Will the truck be able to handle the load?
You whip out your slide rule. You move the cursor to 3.5 on the D scale (recall that the slide rule knows nothing of decimal points; that's up to you). You align the start (1 mark) of the C scale on the slide with the cursor.

You can now read off anything multiplied by 3.5 by reading from the C to the D scale, so you move the cursor to 2.8 on the C scale.

Looking at the D scale, you read 9.8. From the magnitude of the numbers you multiplied, you can easily set the decimal point to the result of 980 kg; the truck can carry the cargo. (How did I set the decimal point? Well, 35 and 28 are around 30, and 30 times 30 is 900, so the result has to be of that magnitude.)
Now this may not seem very magical, but that's because you've never worked out problems like this by long multiplication and division. Being able to get the answer out in a second or two, even with the minor mental gymnastics of setting the decimal point, was a wonder when folks of my generation first encountered it.
Now let's move on to some more complicated problems which show off the capabilities of this implement of math instruction.
Let's start out with a simple physics problem: “How long would the energy of a fastball pitched at 100 miles per hour keep a 100 watt bulb burning if converted to electricity with 100% efficiency?”
The equation for the kinetic energy of a moving body is given by:
![]()
The mass, m, of a baseball is around 145 grams. Since we're asked to compute power in watts, an SI unit, it's easier to start by converting everything into SI units. The mass of the baseball is, then 0.145 kg; this can be worked out trivially in the head. Now we need to convert miles per hour into our value for v in metres per second. Consulting a table of units tells us that a mile is about 1609 metres and an hour is 3600 seconds, so to get v in metres per second we need to compute:
v = (100 miles/hour) × (1609 metres/mile) × (hour/3600 seconds)
Now recall that we don't keep track of decimal places when using a slide rule: that's done mentally or, if it gets messy, with pencil and paper. So, our conversion factor from miles/hour to metres/second is 1609/3600 which, since we only compute to an accuracy of three significant figures, we round off to 161/360. To perform the division, set the cursor to the 1.61 mark on the D scale. Now move the slide to move 3.60 on the C scale under the cursor.

Move the cursor to whichever end of the C scale falls within the D scale. The result of the division, 4.47, can be read off the D scale.

Since by inspection, 161/360 is somewhat less than a half, the decimal point is placed to yield the result, 0.447.
Now we can proceed with the rest of the calculation. First, we need to square the velocity v. Since the velocity was given as 100 miles per hour and we now know the conversion factor, we obtain the velocity as 44.7 metres per second simply by mentally shifting the decimal point two places to the right. To square this value, move the cursor to to 4.47 on the C scale (note that you don't really need to move the cursor, but simply move the slide to the right so the C and D scales are aligned, since the cursor is already at that point on the D scale).

Now flip over the slide rule and read the square, 2.01 from the B scale. Since it's obvious that the square of 40 is 1600, we can place the decimal point to give a value of 2010.

Now we multiply by the mass, m, which is 0.145 kg. Move the cursor to 2.01 on the D scale, then move the slide so the 1 on the C scale lines up with the cursor.

Move the cursor to 1.45 on the C scale and read the product, 2.91, from the D scale.

Since we're multiplying 2010 by a value on the order of 1/10, the decimal point is placed to give a product of 291.
Finally, we need to multiply this value by ½ or, equivalently, divide it by two. We already have the value set up on the D scale, so move the slide to bring 2 on the C scale under the cursor.

Move the cursor to the 1 on the C scale and read off the final result, 1.45.

Since we're dividing a value around 300 by two, the decimal place is set to give 145. The units of this final result are (kilogram metre²)/second², or joules. A watt is just one joule per second, so the answer to the original question is that if the energy of the baseball pitch were converted entirely into electricity, it would keep the 100 watt bulb burning for 1.45 seconds.
A computation of this quantity with a modern computer and double precision arithmetic gives a result of 1.4489 seconds.
The heaviest field artillery piece used by Napoleon's army had a bore diameter of 11.5 centimetres. If it fired spherical iron cannonballs, how much did they weigh?
The formula for the volume of a sphere is:
![]()
Given the 11.5 cm diameter of the bore and the need for the cannonball to fit down it without jamming (neither cannons nor cannonballs were made with great precision at the time), let's assume the cannonballs had a diameter of 11 cm. We need the radius, which we can immediately write down as 5.5 cm without resort to the slide rule. Now we need the cube of this quantity. Move the cursor over 5.5 on the D scale. The cube may then immediately be read on the K scale as 166. Note that the K scale has three decades. The cursor falls within the third decade, indicating the placement of the decimal point.

Now we want to multiply this number by π. Set the cursor to 1.66 on the D scale. We can now immediately read the product of 5.22 from the DF (D Folded) scale, which begins with π. Since the original number was 166, we write the product as 522.

Now set the cursor to 5.22 on the D scale. Move the slide so that 3 on the C scale is under the cursor.

Move the cursor to 1 on the C scale. The quotient of 174 can be read from the D scale, but there's no reason to bother with it, since we're now already set up for the multiplication. Move the cursor to 4 on the C scale. The volume may now be read from the D scale as 696. The decimal position is obvious from the magnitude of the original number before the division and multiplication.

Now we know the volume of the cannonball, 696 cm³. We turn to the Junior Woodchucks' Guidebook to look up the density of iron, which is given as 7.87 g/cm³. To compute the mass of the ball, slide the 1 on the right side of the C scale above the cursor, then move the cursor above 7.87 on the C scale and read the product, 5.47 from the D scale. By inspection of the quantities multiplied, we place the decimal point to give a mass of 5470 grams, or 5.47 kg.

Now, recall that the customary unit of mass, the pound, is around 0.454 kg. Divide the mass we computed, 5.47 by 0.454 (you know how by now, using the C and D scales), and we get around 12 pounds. That's why this gun was called a “twelve pounder!”
Double precision calculation with a modern computer gives a volume of 696.9 cm³, 5.487 kg or 12.098 pounds.
Now let's take our slide rule to the stars—the nearest star: Alpha Centauri, 4.37 light years from the Sun. Let's assume we have a way to accelerate our probe to 90% of the speed of light. How long will it take, measured on-board, for the probe to arrive at its destination?
At speeds close to that of light, the time dilation of special relativity becomes important. Time on board a ship moving close to the speed of light passes slower by a factor of:
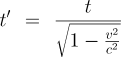
Now, let's get the answer. To simplify, we'll assume the time of acceleration to cruise velocity is negligible compared to the length of the cruise and that the probe will not slow down at the destination.
We can use any units we wish when calculating with a slide rule, so here we'll adopt units where the speed of light is 1; since everything is a fraction of the speed of light, it simplifies things.
First of all, how long will it take, as measured on the Earth, for the probe to arrive at Alpha Centauri? This is easy: the distance is 4.37 light years and the velocity is 0.9 times the speed of light. Set the cursor on the D scale to 4.37 and move the slide to align 9 on the C scale above it.

You can then read out the transit time in Earth co-ordinates as 4.85 years by moving the cursor to the end of the C scale.

Now we need to figure out how much time will have elapsed on board the probe. Since we're computing in fractions of the speed of light, we first square the velocity, 0.9 c. Align the cursor with 9 on the D scale and read the square, 8.1, from the A scale.

Since the quantity squared is close to 1, we place the decimal point to yield 0.81 as the quotient. We subtract this from 1 by hand, yielding 0.19.
Now we require the square root of this quantity. Set the cursor to 19 on the A scale (using the second decade on the right due to the magnitude of the quantity), and read off 4.35 on the D scale as the square root.

This is the factor of time dilation which, placing the decimal point, is 0.435. We can now multiply the length of the trip as measured on Earth to obtain the time measured on board the ship. Move the cursor to 4.85 on the D scale (transit time as measured on Earth), then move the slide to align 1 on the right side of the C scale with the cursor.

Finally move the cursor to 4.35 on the C scale to read off the ship's clock time, 2.11 years, from the D scale.

A modern computer calculation yields a transit time as measured from Earth as 4.86 years and time measured by the ship's clock as 2.12 years.
If you want to further explore this forgotten skill, you'll find many vintage slide rules for sale on eBay (don't become a collector; it can ruin your life!). The basics of slide rule computations are explained in this tutorial. The International Slide Rule Museum has a multitude of resources for slide rule fans, including scans of user manuals from a variety of manufacturers. Here is a virtual slide rule which works in your browser.
Here are two videos (with regrettable autofocus hunting) explaining the basics of computation with a slide rule.
This is a somewhat tedious 1943 U.S. government training film on multiplication and division with the slide rule.
A 1944 sequel covers more complicated calculations including proportion, percentages, squares, and square roots.
This document is in the public domain.