|
|
The purpose of computing is insight, not numbers.—Richard W. Hamming, 1962
The rubber bag explains the mechanics of gaining and losing weight. But
why can some people control their weight effortlessly while others
seem locked in a lifelong struggle against obesity? To understand
this and find a path to permanent weight control, we must again
step back from the daunting complexity of the human body and seek
enlightenment from a much simpler model. Consider how a thermostat
controls the temperature.
To control something, first we have to be able to measure it. To control temperature, start with a thermometer.
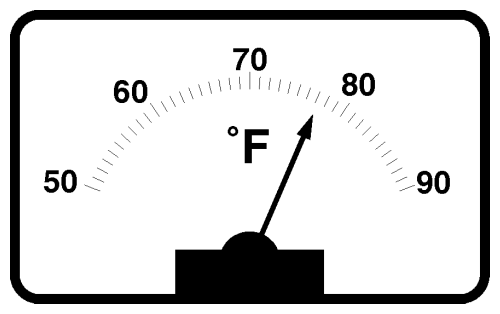
A thermometer tells precisely how miserable the weather is but doesn't do anything about it. Here's an example of the information the thermometer provides: the outside temperature over a day, plotted every 10 minutes.
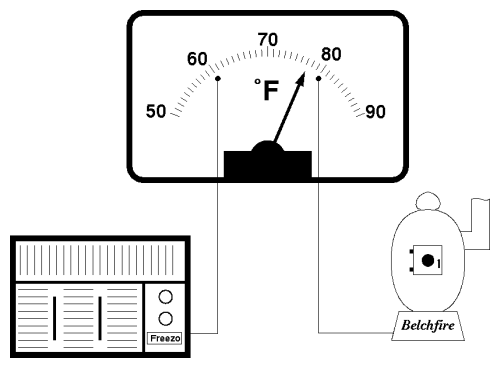
The next step toward controlling something is choosing the objective, expressed in terms of the numbers we're measuring. Suppose we'd like to arrange things so the house never gets colder than 60° Fahrenheit nor warmer than 80° . We can modify the thermometer by adding electrical contacts at the 60 and 80 degree points on the scale, like this.
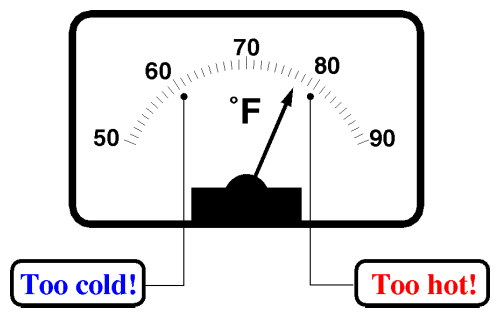
When the needle touches one of these contacts, it will close a circuit. The circuit remains closed as long as the temperature is outside the range of 60 to 80 degrees. We can wire this modified thermometer up to a pair of indicator lights. When the temperature drops below 60° the “Too cold!” light will come on, and when it exceeds 80°, the “Too hot!” indicator illuminates.
This apparatus monitors the temperature, detects when it's outside the range we're happy with, and lets us know what the problem is (too hot or too cold). We can think of this refinement as having drawn limit lines on the temperature graph, like this.
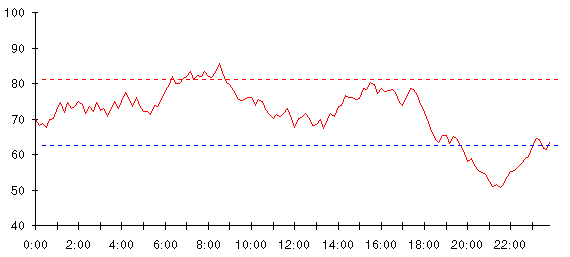
Whenever the temperature is above the top line, the Too hot! light will go on, and whenever it falls below the bottom line, Too cold! will be signaled.
Whenever the “Too cold!” light comes on, we could stoke up the furnace, and when “Too hot!” was lit, crank up the air conditioner. But why get personally involved? We can wire the furnace and air conditioner right up to the thermometer in place of the blinkin' lights.
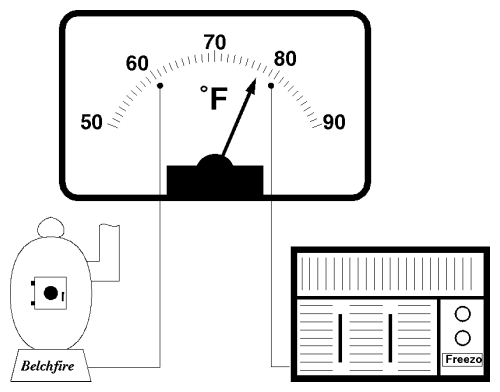
Whenever the temperature drops to 60 or below, the heater starts up and keeps on running until it's raised the temperature above 60, switching it off. When the needle hits 80, the air conditioner whirrs into action and wafts a welcome, cooling zephyr our way until the temperature falls back below that mark.
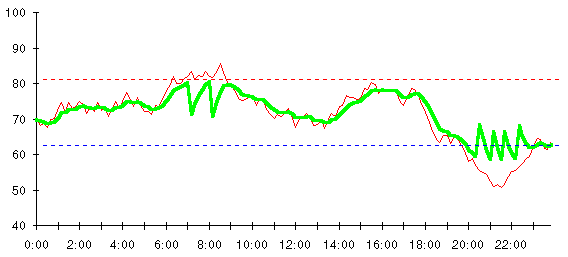
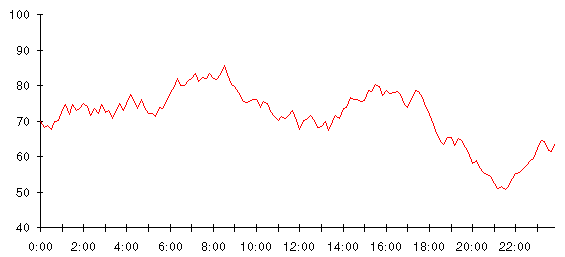
Finally, we've achieved control over the temperature. The heavy line on this chart is the indoor temperature. As long as the outside temperature stays between 60 and 80 degrees, the indoor temperature follows it. As soon as the temperature begins to drift outside this range, the furnace or air conditioner pulls the temperature back toward the goal of 70° .
Engineers call this “negative feedback.” The phrase is important, so let's pick it apart word by word. “Feedback” refers to the process by which the measurement (temperature) causes actions (starting the furnace or air conditioner) which, in turn, affect the quantity we're measuring (by heating or cooling the room). The feedback is “negative” because the action opposes the condition that triggers it. When it's too cold, the furnace heats up the place. When it's too hot, the air conditioner comes on and cools things off—negative feedback.
Another way of thinking about feedback is in terms of the constraints it places on the freedom of the system to change. Think of the temperature the thermostat is controlling as a ball rolling on a surface. As long as no feedback is applied, the ball is free to roll whenever it likes: the surface can be thought of as a completely flat plain, like this.
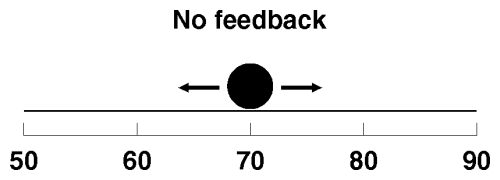
When it gets warmer outside, the ball, representing room temperature, gets pushed to the right, toward higher readings. When it cools off, the ball is dragged back to the left. In neither case does the ball “push back”; it moves totally at the whim of the weather.
Providing negative feedback with a thermostat changes the lay of the land. Instead of the temperature roaming freely like a ball on a flat surface, now it's confined within a valley.
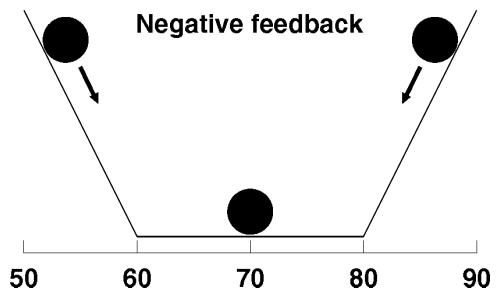
The flat floor of the valley represents temperatures between 60 and 80 degrees. Within this range the ball, representing the temperature, is free to follow the outside temperature as before. Once it reaches the point where the thermostat starts heating or cooling the room, however, it encounters a steep slope. As long as the heating or cooling capacity exceeds the rate heat can leak through the walls from outdoors, the temperature will remain confined to the desired range. This viewpoint makes the stability conferred by negative feedback self-evident.
Negative feedback is at the heart of every stable, self-regulating system. If a company raises prices too high, people stop buying and soon the company cuts the price to increase sales. When there's plenty of rabbits, the wolves eat well, multiply, and before long more rabbits get eaten and they aren't so abundant. When your car starts veering into the left lane, you turn the wheel to the right. When you're feeling tired, you get more sleep. Negative feedback is ubiquitous, yet its profound consequences are often overlooked for this very reason. To understand them better, consider what happens when feedback goes bad.
Suppose the electrician or somebody like him makes a little boo-boo in hooking up the thermostat. Instead of the way we designed it, he wires it like this.
As long as the temperature stays between 60 and 80, everything will be fine. On the coast of Northern California where I'm writing this book, months may pass before the error is discovered. One bright October day, however, the temperature will creep up to the 80 mark. And then, all Hell breaks loose. With a Whoomp, the furnace lights off and starts doing its best to “remedy” the situation. Before long the house is transformed into a broiling pan, a blast furnace, a simulacrum of summer in New Jersey (albeit without the crummy bugs). Should a chilly July day drop the temperature below 60, the inverse scenario plays out. The air conditioner springs into action, commanded by positive feedback to create its own little polar ice cap in your living room. Mush!
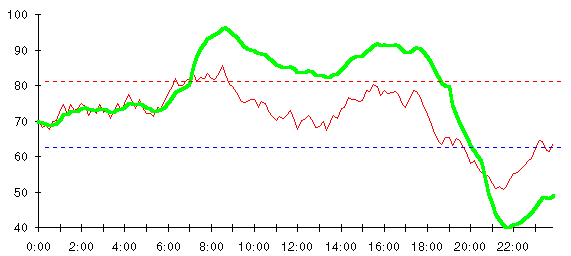
Here's how the temperature behaves when the thermostat's wired for positive feedback. As long as the temperature remains between 60 and 80 degrees, all is well. As the sun rises, however, the temperature crosses the 80 degree mark and the furnace starts. This quickly pushes the temperature up near the century mark and the furnace continues to roar, compounding the problem, most of the day. Only in the evening does the rapidly falling outside temperature drag the indoor temperature below 80 degrees, finally shutting off the heat. Unfortunately, the temperature soon falls below 60 and the air conditioner starts. Temperatures plunge and finally hit 40. The only thing that keeps the temperature from rising to the point of ignition or falling until the air is liquefied is the finite capacity of the furnace to heat and the air conditioner to cool, plus leakage of heat to and from the outside.
Again, consider the temperature as a ball rolling over terrain. In the absence of feedback, the terrain was flat. Negative feedback confined the ball to a valley. With positive feedback the ball rests atop a hill:
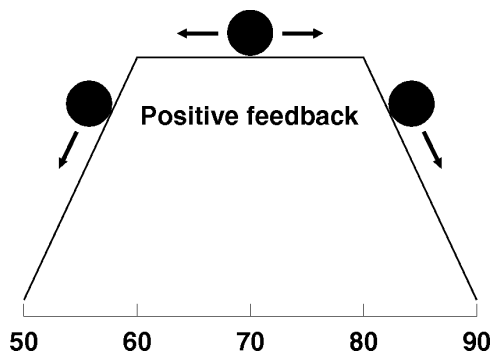
As with negative feedback, the ball is free to roam within the flat region. Upon reaching the edge, however, rather than being pushed back as negative feedback would do, positive feedback forces it further outside the stable region. In other words, once the ball rolls off the flat crest of the hill, it rolls downhill faster and faster. The system can be returned to the stable region only by pushing the ball uphill against the force of positive feedback.
When things shrug off the bonds of control and start to get weird, positive feedback is usually in the driver's seat. The very word “feedback” means, to many people, one of the most common examples of positive feedback: the deafening scream when a microphone picks up a sound from a speaker and sends it back to the speaker which emits it even louder, which is picked up by the microphone….
Positive feedback makes for humorous anecdotes. But the real world contains, sadly, many examples of positive feedback put in place by well-meaning politicians and businessmen who don't understand the consequences of crossing the wires between noble ends and expedient means. Consider the nuclear arms race. At the end of World War II, the United States and Britain realised they couldn't afford to match the Soviet army in Europe so they built nuclear bombs and threatened all-out destruction of the Soviet homeland in response to any aggression. The Soviets, faced with the ultimate threat, accelerated their own nuclear program in the belief that only by matching or surpassing the West could they deal on an equal basis. Once the Soviets tested their bomb, hysteria in the West was compounded—now they faced an adversary armed with the Bomb as well as a huge army. The only way to deter the Soviets from using their bomb was to build mo' bigger bombs. And so on, as fear fed on fear, technological developments like the ballistic missile spurred further developments and countermeasures by the other side, the whole process consumed a substantial fraction of all the world's wealth for decades. This tragedy of our age is, at its heart, a case of positive feedback, pure and simple. And like most examples of positive feedback it was stopped (if indeed it has ceased and not just gone on vacation), not by good will, not through mutual understanding and trust, not by the actions of diplomats and politicians, but by the application of stronger negative feedback. The negative feedback in the arms race was economic: the race grew to the point where it virtually bankrupted the participants who were, only then, compelled to slow down.
Once you begin to analyse things in terms of positive and negative feedback, you'll never see things quite the same.
Our thermostat, regardless of whether it's wired for negative or positive feedback, applies an all or nothing form of control. When the temperature drops too low, the furnace comes on, Hell bent, to heat up the place. When it gets too hot, the air conditioner's unleashed, flat out, to chill out the environs.
Engineers call this kind of control “bang-bang.” When it gets too cold bang, the furnace comes on. As soon as the temperature rises above 60°, bang the furnace cuts off. Too hot? Bang, the air conditioner starts, and so on.
Take a closer look at the inside temperature in the chart above. See how the temperature tends to oscillate between 70 degrees and the level where the thermostat kicks in? That's the signature of bang-bang control—since nothing happens until one of the limits is hit, the temperature varies freely between them. When the system exceeds a limit, it's hauled back within range, then allowed to drift again.
Bang-bang control keeps the temperature pretty much within the range from 60 to 80, but it allows the temperature to vary freely between the limits. Suppose instead of just switching the furnace and air conditioner on and off, we coupled the temperature reading to the gas valve on the furnace: the further the temperature falls below 70, the more heat the furnace generates. Likewise, as soon as the temperature rises above 70, the air conditioner starts, but we rig it to generate more and more cooling as the temperature rises. We'll end up with a system that behaves like this.
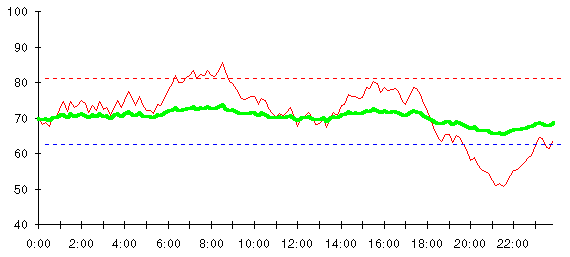
This is called proportional control. The action taken, the feedback, is in proportion to the degree the system diverges from the ideal point. Imagine you're driving down the road some lonely night. Proportional control is how you usually drive; every time you notice the car drifting a tiny bit to the left, you steer slightly to the right and vice versa. Bang-bang control would mean ignoring the steering wheel until the car crossed a lane marker line. Then you'd haul it in the opposite direction until the car was no longer outside the lane: exciting, perhaps, but not recommended.
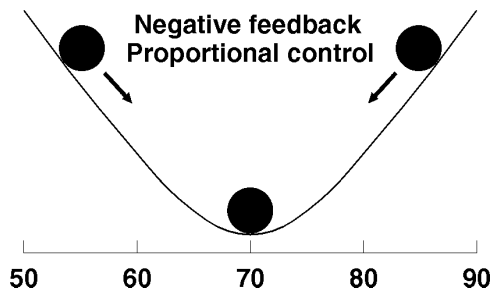
If bang-bang negative feedback keeps the temperature ball on the flat floor of a valley with steep sides (see the negative feedback chart), proportional control confines it to the bottom of a smoothly sloped bowl. The slightest degree of motion away from the optimal point, the bottom of the bowl, causes the ball to roll upward. The further it deviates from the goal, the stronger the force applied to restore it—back to the bottom of the bowl. A chart of positive feedback with proportional control would simply flip the bowl upside down: the temperature would remain stable only as long as it stayed perched at the precise optimum point. To appreciate how quickly proportional positive feedback gets out of hand, try balancing a raw egg on top of a bowling ball.
Proportional control makes systems run smoother than bang-bang. Most biological systems are proportional, while many engineered and all too many political and social systems are bang-bang. As with negative and positive feedback, once you understand how proportional control lends stability to a system, while bang-bang tends to oscillate between the extremes, you'll recognise many examples of both kinds of control in everyday life.
A wise engineer once said that all systems, regardless of composition, do one of three things: blow up, oscillate, or stay about the same. Once you understand feedback, you know why this must be. If a system blows up, it is governed by positive feedback. If it stays about the same, negative feedback is on the job. If it oscillates, either negative or positive feedback can be in charge. You have to look more closely at the details.
Feedback doesn't explain everything, but it explains a great many things. Let us now turn to how and why these three forms of behaviour: stability, oscillation, and runaway growth, are literally embodied in human beings.
“Enough with the thermostats, already!” you shriek, exasperated. “I'm not too cold, I'm too fat! What does all this have to do with losing weight?”
Patience, please. The problem isn't losing weight, it's gaining weight. If you hadn't already gained more weight than you're happy toting around, you wouldn't be reading a diet book. Anybody can lose weight…for a while. Many of us have lost weight on numerous occasions, only to put it right back on within a short time. The problem isn't weight loss, it's weight control, and the insights into feedback and control from the thermostat were necessary to allow us, finally, get a handle on our problems with weight.
It's time to stop talking about the weather and start doing something about what we weigh.
Consider Skinny Sam, that exasperating acquaintance we all seem to have: the fellow who's never overweight, never out of shape, who chows down whenever he feels like and eats as much as he wants, who can't understand how anybody could have a weight problem. How does he do it?
Well, now we know. Sam is fortunate enough to possess a mechanism you and I lack: a proportional negative feedback linkage between his body's need for calories and his appetite for food. His feedback system works like this.
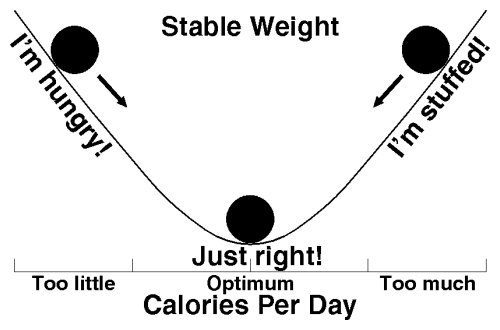
This graph is identical to the one describing a proportional control thermostat; compare it with the proportional feedback chart. The mechanism is identical, only the labels have been changed to reflect the incidents. Rather than temperature, what's being controlled is the number of calories of food eaten. Rather than switching on a furnace or air conditioner, control is accomplished through a signal called appetite. The effect is the same.
When Sam eats the same number of calories as he burns, the ball rests at the bottom of the bowl and his appetite is silent. If less food goes in than he burns, whether from skipping meals, eating less at each meal, or from the extra calories he burns up practicing wolverine juggling three times a week, the ball drifts to the left. As it does, his appetite begins to signal, subtly at first then with increasing stridency, the need for more food. Conversely, when too many working lunches become rounds of “eat fast or get the anchovies”; when Sunday afternoon touch football in the back yard is supplanted by Monday Night Football in front of the illuminatus, too many calories begin to push the ball to the right. “How can you think of food?”, groans Sam. “You guys enjoy your burgers. All I want is a stalk of celery and a good night's sleep!”
To fully understand the difference between Skinny Stable Sam and ourselves, it's necessary to consider the rubber bag again. Sam's feedback system connects calories eaten to appetite. It does not connect weight to appetite. Failing to appreciate this distinction has led millions of dieters to fail. Remember the rubber bag. For the most part it doesn't matter how much you weigh; whether you gain or lose weight depends only on the balance between calories eaten and calories burned.
One encouraging conclusion can be drawn from this: you won't be any more hungry at your optimal weight than at any weight above it. The rubber bag cares only about the difference between what goes in and what goes out. So don't assume that being thin dooms you to a life of endless hunger. You now understand enough of what's going on to see what utter, discouraging bilge that suggestion is.
Consider how Sam's body reacts when it gets too much or too little food. Assume Sam's normal weight is 150 pounds.

Here the horizontal axis represents the number of calories eaten per day, with the centre point, “Ideal calorie intake,” the amount Sam burns per day. The rubber bag, like most models, doesn't precisely represent the underlying reality: the human body. It isn't necessary to exactly balance calories eaten with calories burned. If you eat a little too much, the body cranks up the burn rate a little: you feel warmer and more inclined to run up a flight of stairs rather than walk. If you eat a tad less than ideal, you may feel chilly and inclined to curl up with a book under the blankets and get a little extra sleep.
This is the lowest level of proportional weight control, and it works for all of us. It means that there's no need to become obsessed with matching calories eaten and burned; it's only when the balance shifts decisively and consistently to one side or the other of the ideal calorie intake that we get into trouble.
The vertical axis makes it clear what that trouble amounts to. The rubber bag expands or shrinks: we gain or lose weight. Once what goes into the rubber bag exceeds your capacity to crank up the heat, the excess starts showing up as fat. Similarly, to achieve weight loss, you have to reduce what goes in below your capacity to adjust by banking the metabolic fires, forcing your body to tap its reserves: to burn fat and thereby shrink the rubber bag.
To complete our understanding of how feedback keeps Sam's weight under control, let's overlay the graph that shows how calories affect weight and the chart of feedback from calorie consumption to appetite.

The feedback, neatly centred around the ideal calorie intake, keeps the calories eaten within the region that changes in metabolism can adapt to. Since feedback balances what goes into the rubber bag with what's burned, weight remains constant. When Sam eats a bit too much or too little his metabolism adjusts, as does ours. But, if he goes beyond that point, his appetite begins to tell him to eat more or less before the shortfall or excess shows up on the scale or the waistline.
Ahhhh, Sam…, if you only knew the thoughts that run through our minds. Sam's got it made. But for those of us who don't the real question is what it is Sam has that we're lacking. And that's now clear: a built in eat watch—a proportional negative feedback system that adjusts what he eats, by controlling appetite, to equal what his body burns. We're missing that negative feedback system. Should we begrudge Sam his genetic advantage and accustom ourselves to overweight, or just fix the system? Fix it, of course! But first, let's consider what happens when it's broken.
Many of us live the life of Oscar or at least know somebody like him. Oscar's always on a diet. “Gotta take off five pounds” he chants, like a mantra, although he usually runs about twenty pounds overweight. Funny thing is, every time you go out to eat with Oscar, he seems to eat less than anybody. He is, after all, dieting.
Skinny Sam is a gentleman and a scholar and would never countenance such thoughts but Lanky Lunkhead, having never read this book, frequently suggests behind Oscar's back that perhaps the odd midnight indulgence in peanut butter, salami, swiss cheese, avocado, fried egg, onion, and tomato sandwiches accounts for Oscar's perennial weight problem. Notwithstanding Lanky's sublimated craving for such delicacies, Oscar is simply struggling with a different feedback system.

Oscar has the very same feedback curve as Sam, but his is shifted a little to the right, toward eating too much. One day Sam eats slightly more than he needs, and the next day slightly less. But since feedback keeps him within the range his metabolism can adjust to, Sam's weight stays the same. When Oscar eats slightly too much, though, he's pushed immediately into the region where he packs on weight. The next day, like Sam, he may eat less but, since that's within the flat part where metabolism compensates, he keeps all the weight he packs on whenever he eats a little too much.
The shift in Oscar's feedback curve with respect to his body's need for calories acts as a ratchet; each excess runs his weight up, but equivalent shortfalls don't burn off the excess weight. Over time, Oscar begins to see the evidence of this on the scale and in how his clothes fit. Having lived with this condition all his life, Oscar knows there's only one solution: peel off the pounds. So, for the umpty-umpth time he embarks on a diet: perhaps a sure-fire plan that's worked before, or maybe the current rage all the celebrities are swearing by. “Peach fuzz, eh? Sounds promising….”
Reducing is miserable for Oscar. In order to lose weight, he must reduce what goes in far enough to get into the “Lose weight” area of the curve. But that means the ball on the feedback chart has to climb well into the “I'm hungry!” region and stay there for an extended time. Over the years, Oscar has integrated this viewpoint into his self-image, “If I eat reasonably, I gain weight. Then I have to endure hunger just to get back where I started.” What Oscar doesn't realise is that his problem is simply poor feedback from the calories he needs to his appetite. If he got accurate feedback, as Sam does, he'd never eat too much, feel hungry, or be forced to endure hunger to take off extra weight. Oscar's built-in eat watch is simply set 5 minutes too fast. Oscar needs to wear an accurate eat watch to put an end to his oscillations.
Bulky Buster envies Oscar. Buster's big, and with every passing year he seems to get a little bigger. For the most part he's healthy, although he gets winded easily, and happy, though he'd certainly rather not worry about his weight every day. Buster knows the odds: he's seen those “Calculate your lifespan” tables and even worked them out on occasion. Indeed, five years of life would be a wonderful reward for getting rid of those fifty extra pounds, if only there were any way of doing that. Disgust with being overweight, resolve to reduce, commitment to a plan…failure to keep the weight off, acceptance of failure as inevitable, resignation to a lifetime of overweight, denial of the consequences, surrender to the temptation of food: Buster has trodden this circle many times in attempts to control his weight. Why is it so hard for him? We need only look at his feedback chart.
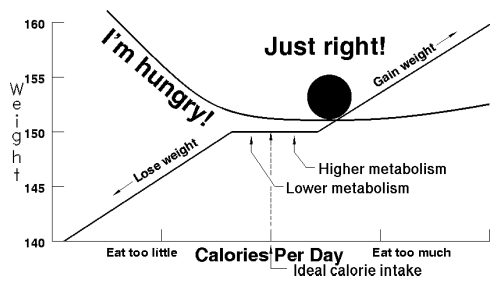
Buster gets a clear signal every time he eats too little, but never hears a thing when he eats too much, unless it's enough to actually make him sick. Like Sam, like Oscar, like all of us, from time to time Buster's inclined to overeat. But nothing tells him to stop; not then, and not the next day. The extra calories show up, not as reduced appetite to compensate, but as pounds on the scale. Once that excess is stored as fat, the only way Buster can burn it off is by going hungry.
Buster feels like he's been dealt a lousy hand by life, and he's absolutely right. When he eats too little, he gets squawks from the stomach just as loud as Skinny Sam does, but when he errs on the other side, no alarm goes off. Many problems with Buster's feedback system can cause this, but the result is the same. While Oscar slowly drifts toward overweight, Buster feels himself on a Hellbound train, utterly unable to understand why he consistently packs on weight and powerless to control it other than by periods of deliberate starvation.
I do not mean to put down Buster! I spent most my life in this precise pattern of behaviour. What's “wrong with Buster” isn't a flaw of character. He's not inferior. He's just wired up wrong and, once he understands the problem as we now do, he can fix it.
One can imagine, before eyeglasses were invented, a culture that exalted those with 20/20 vision and disdained others who had difficulty seeing distant objects. (Imagine? Try becoming an airline pilot if your vision isn't perfect without glasses.) Poor vision might be attributed to “flabby eyes,” resulting from a lack of visual exercise. (The quack Bates method of vision correction persists in claiming this today).
Yet what distinguishes the near- and farsighted from those with perfect vision is but a minor difference in the shape of the lens in the eye. Before corrective lenses, those who couldn't see clearly were indeed handicapped. Think about it; would you be better off with one arm and able to see clearly, or with two arms but unable to focus on anything more than six inches from your face?
If Buster were born nearsighted, he'd wear glasses or contacts and never imagine himself a lesser man for doing so. He'd laugh, along with everybody, at a fool who suggested he throw away his glasses and apply all his will power to developing, instead, a “natural sense of sight.” And yet Buster's weight problem, like Oscillating Oscar's and yours and mine stems from just as simple a biological shortcoming as poor eyesight. Buster's built-in eat watch runs too fast, and as long as he relies on it he'll go on gaining weight. To solve his problem, he doesn't need to feel guilty, develop a “stronger character,” or change his lifestyle, any more than any of those things would have cured his myopia. No, Buster, like Oscar, like you and I, simply needs an eat watch to give him the feedback his body doesn't.
There are many ways in which an individual's appetite feedback curve can be related to calorie requirements but, as noted by the engineering aphorism, only three possible outcomes. Weight can blow up (gain constantly, like Buster), oscillate (Oscar's lose/gain rollercoaster, so familiar to many of us), or stay about the same (lucky Sam). If you flip the feedback curves in these charts left for right, you have depictions of an anorexic, an individual who tends to lose weight, and Sam. A multitude of reasons: organic, cultural, and psychological, may explain why feedback fails in certain people. Many diet books counsel searching yourself for the underlying causes of weight gain and remedying them. This may be an interesting and rewarding process, but it's no way to lose weight. It's kinda like becoming an expert watchmaker to fix your Timex that keeps stopping and nobody can seem to repair. The wiser man buys a new watch.
The temperature charts used as illustrations in this chapter were made with a mathematical model of the thermostat system implemented in Excel. Playing around with this model, entering different values that control the feedback, will give you an excellent feel for the kinds of behaviour a system exhibits in the presence of various kinds of feedback.
To experiment with this model, load the Excel worksheet FEEDLAB.XLS. Depending on the display board and monitor your computer is equipped with, you may have to resize the window in order to see the entire worksheet as shown below.
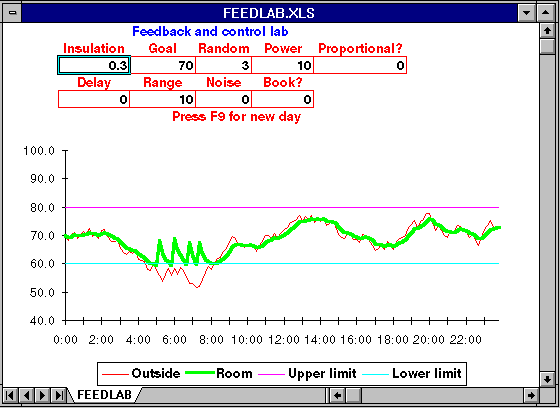
The outside temperature is shown as a thin red line and the inside temperature as a thicker green line. The outside temperature is generated randomly. Every time you enter a number in the control panel, a new outside temperature profile is generated. You can test the existing system with a different data by pressing F9. Each time you push it a new temperature database is generated.
The temperature data used by the charts in this chapter are included in the FEEDLAB spreadsheet. If you enter 1 in the Book? cell, the book data are used rather than randomly generated temperatures. To return to using random data, enter 0 in this cell.
The other boxes in the control panel specify the parameters of the system as follows.
Proportional. If this cell is 0, the system is bang-bang: the heater is activated only when room temperature falls below the light blue line and the air conditioner only when it exceeds the purple upper limit line. If you enter 1, heating and cooling are used whenever the temperature diverges from the value in the Goal cell, adjusted proportionally based on how far it is from that value. For proportional control, the maximum capacity specified by Power is reached at the limit lines.
Goal. This is the temperature at which the thermostat attempts to maintain the room.
Range. The value in this cell determines how many degrees from the Goal the temperature is permitted to vary before heating or cooling is triggered (if Proportional is 0), or reaches maximum Power (if Proportional is 1). If the Goal temperature is 70° and Range is 10, the temperature limits will be 60° and 80° .
Power. This controls the rate of heating and cooling available, in terms of degrees of change in each 10 minute interval. If you set Power to 0, the heater and air conditioner will have no effect when activated and room temperature will track outside temperature. (Try it.) If you set Power negative, the furnace cools and the air conditioner heats—this rigs the system for positive feedback. Positive feedback from negative Power settings combined with proportional control will usually drive the temperature into wild oscillations.
Random. The amount of daily temperature variation is controlled by this value. It specifies how many degrees the outside temperature can change in a 10 minute interval. For example, if it's currently 75 degrees and Random is set to 3, the temperature at the next 10 minute mark will be picked at random between 72° and 78°. If you set Random to 0, the outside temperature remains constant.
Insulation. The value in this cell expresses how well the room is insulated in terms of the rate at which heat leaks through the walls to and from the outside. Insulation of 0 specifies a perfectly insulated room; changes in the temperature outdoors don't have any effect on the temperature inside. An Insulation value of 1 means total leakage to the outside: a three degree change outdoors will cause an identical change within the room, unless counteracted by the furnace or air conditioner.
Noise. As long as this cell is 0, the thermostat bases its actions on perfectly accurate measurements of temperature. You can observe the effects of random measurement errors by setting Noise to the extent of the error range in degrees. For example, if the temperature is actually 70 degrees and Noise is set to 5, the thermostat will act based on a reading randomly picked between 67.5° and 72.5° . The Noise affects every measurement, perturbing each randomly within the specified range. Nonzero Noise settings allow you to see how inaccurate measurements can trigger destructive positive feedback.
Delay. If this cell is 0, the thermostat measures temperature instantaneously and immediately takes whatever action is indicated. You can introduce delay between measurement and action by setting Delay to the number of 10 minute intervals that elapse between the measurement and the corresponding action. The propensity that delay has to drive even systems with strong negative feedback into oscillation, particularly those with proportional control, can be seen by setting Delay to 1, 2, or 3. Larger values than that make the temperature oscillate even more wildly.
Mathematical details of this model are given in the section “Calculating feedback models”.
|
|