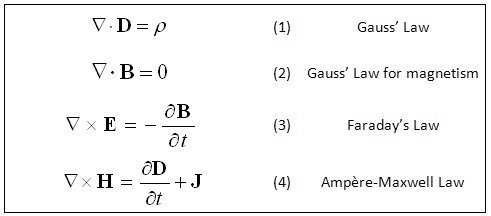« November 2, 2018 | Main | November 6, 2018 »
Saturday, November 3, 2018
Reading List: The Forgotten Genius of Oliver Heaviside
- Mahon, Basil. The Forgotten Genius of Oliver Heaviside. Amherst, NY: Prometheus Books, 2017. ISBN 978-1-63388-331-4.
-
At age eleven, in 1861, young Oliver Heaviside's family,
supported by his father's irregular income as an engraver of
woodblock illustrations for publications (an art beginning to be
threatened by the advent of photography) and a day school for
girls operated by his mother in the family's house, received a
small legacy which allowed them to move to a better part of
London and enroll Oliver in the prestigious Camden House School,
where he ranked among the top of his class, taking thirteen
subjects including Latin, English, mathematics, French, physics,
and chemistry. His independent nature and iconoclastic views
had already begun to manifest themselves: despite being an
excellent student he dismissed the teaching of Euclid's geometry
in mathematics and English rules of grammar as worthless. He
believed that both mathematics and language were best learned,
as he wrote decades later, “observationally,
descriptively, and experimentally.” These principles
would guide his career throughout his life.
At age fifteen he took the College of Perceptors examination,
the equivalent of today's A Levels. He was the
youngest of the 538 candidates to take the examination and
scored fifth overall and first in the natural sciences. This
would easily have qualified him for admission to university,
but family finances ruled that out. He decided to
study on his own at home for two years and then seek a job,
perhaps in the burgeoning telegraph industry. He would receive
no further formal education after the age of fifteen.
His mother's elder sister had married
Charles
Wheatstone, a successful and wealthy scientist, inventor,
and entrepreneur whose inventions include the concertina,
the stereoscope, and the Playfair encryption cipher, and who
made major contributions to the development of telegraphy.
Wheatstone took an interest in his bright nephew, and guided
his self-studies after leaving school, encouraging him
to master the Morse code and the German and Danish languages.
Oliver's favourite destination was the library, which he later
described as “a journey into strange lands to go a
book-tasting”. He read the original works of
Newton, Laplace, and other “stupendous names”
and discovered that with sufficient diligence he could
figure them out on his own.
At age eighteen, he took a job as an assistant to his older
brother Arthur, well-established as a telegraph engineer in
Newcastle. Shortly thereafter, probably on the recommendation
of Wheatstone, he was hired by the just-formed
Danish-Norwegian-English Telegraph Company as a telegraph
operator at a salary of £150 per year (around £12000
in today's money). The company was about to inaugurate a cable
under the North Sea between England and Denmark, and Oliver set
off to Jutland to take up his new post. Long distance telegraphy
via undersea cables was the technological frontier at the time—the
first successful transatlantic cable had only gone into
service two years earlier, and connecting the continents into
a world-wide web of rapid information transfer was the
booming high-technology industry of the age. While the job
of telegraph operator might seem a routine clerical task,
the élite who operated the undersea cables worked in
an environment akin to an electrical research laboratory,
trying to wring the best performance (words per minute) from
the finicky and unreliable technology.
Heaviside prospered in the new job, and after a merger
was promoted to chief operator at a salary of £175
per year and transferred back to England, at Newcastle.
At the time, undersea cables were unreliable. It was not
uncommon for the signal on a cable to fade and then die
completely, most often due to a short circuit caused by failure
of the
gutta-percha
insulation between the copper conductor and the iron sheath
surrounding it. When a cable failed, there was no alternative
but to send out a ship which would find the cable with a
grappling hook, haul it up to the surface, cut it, and test
whether the short was to the east or west of the ship's
position (the cable would work in the good direction but
fail in that containing the short. Then the cable would be
re-spliced, dropped back to the bottom, and the ship would
set off in the direction of the short to repeat the exercise
over and over until, by a process similar to
binary
search, the location of the fault was narrowed down and
that section of the cable replaced. This was time consuming
and potentially hazardous given the North Sea's propensity
for storms, and while the cable remained out of service it
made no money for the telegraph company.
Heaviside, who continued his self-study and frequented the
library when not at work, realised that knowing the resistance
and length of the functioning cable, which could be easily
measured, it would be possible to estimate the location of
the short simply by measuring the resistance of the cable
from each end after the short appeared. He was able to
cancel out the resistance of the fault, creating a quadratic
equation which could be solved for its location. The first
time he applied this technique his bosses were sceptical,
but when the ship was sent out to the location he
predicted, 114 miles from the English coast, they quickly
found the short circuit.
At the time, most workers in electricity had little use for
mathematics: their trade journal, The Electrician
(which would later publish much of Heaviside's work) wrote in
1861, “In electricity there is seldom any need of
mathematical or other abstractions; and although the use of
formulæ may in some instances be a convenience, they may
for all practical purpose be dispensed with.” Heaviside
demurred: while sharing disdain for abstraction for its own
sake, he valued mathematics as a powerful tool to understand
the behaviour of electricity and attack problems of
great practical importance, such as the ability to send
multiple messages at once on the same telegraphic line and
increase the transmission speed on long undersea cable links
(while a skilled telegraph operator could send traffic
at thirty words per minute on intercity land lines,
the transatlantic cable could run no faster than eight words
per minute). He plunged into calculus and differential
equations, adding them to his intellectual armamentarium.
He began his own investigations and experiments and began
to publish his results, first in English Mechanic,
and then, in 1873, the prestigious Philosophical
Magazine, where his work drew the attention of two of
the most eminent workers in electricity:
William Thomson (later Lord Kelvin) and
James Clerk Maxwell. Maxwell would go on
to cite Heaviside's paper on the Wheatstone Bridge in
the second edition of his Treatise on Electricity
and Magnetism, the foundation of the classical
theory of electromagnetism, considered by many the greatest
work of science since Newton's Principia,
and still in print today. Heady stuff, indeed, for a
twenty-two year old telegraph operator who had never set
foot inside an institution of higher education.
Heaviside regarded Maxwell's Treatise as the
path to understanding the mysteries of electricity he
encountered in his practical work and vowed to master it.
It would take him nine years and change his life. He
would become one of the first and foremost of the
“Maxwellians”, a small group including
Heaviside, George FitzGerald, Heinrich Hertz, and Oliver
Lodge, who fully grasped Maxwell's abstract and highly
mathematical theory (which, like many subsequent milestones
in theoretical physics, predicted the results of experiments
without providing a mechanism to explain them, such as
earlier concepts like an “electric fluid” or
William Thomson's intricate mechanical models of the
“luminiferous ether”) and built upon its
foundations to discover and explain phenomena unknown
to Maxwell (who would die in 1879 at the age of just 48).
While pursuing his theoretical explorations and publishing
papers, Heaviside tackled some of the main practical problems
in telegraphy. Foremost among these was “duplex
telegraphy”: sending messages in each direction
simultaneously on a single telegraph wire. He invented a
new technique and was even able to send two
messages at the same time in both directions as fast as
the operators could send them. This had the potential
to boost the revenue from a single installed line by
a factor of four. Oliver published his invention, and in
doing so made an enemy of William Preece, a senior engineer
at the Post Office telegraph department, who had invented
and previously published his own duplex system (which would
not work), that was not acknowledged in Heaviside's paper.
This would start a feud between Heaviside and Preece
which would last the rest of their lives and, on several
occasions, thwart Heaviside's ambition to have his work
accepted by mainstream researchers. When he applied to
join the Society of Telegraph Engineers, he was rejected
on the grounds that membership was not open to “clerks”.
He saw the hand of Preece and his cronies at the Post Office
behind this and eventually turned to William Thomson to
back his membership, which was finally granted.
By 1874, telegraphy had become a big business and the work
was increasingly routine. In 1870, the Post Office had
taken over all domestic telegraph service in Britain and,
as government is wont to do, largely stifled innovation and
experimentation. Even at privately-owned international
carriers like Oliver's employer, operators were no longer
concerned with the technical aspects of the work but rather
tending automated sending and receiving equipment. There
was little interest in the kind of work Oliver wanted to do:
exploring the new horizons opened up by Maxwell's work. He
decided it was time to move on. So, he quit his job, moved
back in with his parents in London, and opted for a life
as an independent, unaffiliated researcher, supporting himself
purely by payments for his publications.
With the duplex problem solved, the largest problem that
remained for telegraphy was the slow transmission speed on long
lines, especially submarine cables. The advent of the telephone
in the 1870s would increase the need to address this problem.
While telegraphic transmission on a long line slowed down the
speed at which a message could be sent, with the telephone voice
became increasingly distorted the longer the line, to the point
where, after around 100 miles, it was incomprehensible. Until
this was understood and a solution found, telephone service
would be restricted to local areas.
Many of the early workers in electricity thought of it as
something like a fluid, where current flowed through a wire like
water through a pipe. This approximation is more or less
correct when current flow is constant, as in a direct current
generator powering electric lights, but when current is varying
a much more complex set of phenomena become manifest which
require Maxwell's theory to fully describe. Pioneers of
telegraphy thought of their wires as sending direct
current which was simply switched off and on by the sender's
key, but of course the transmission as a whole was a varying
current, jumping back and forth between zero and full current at
each make or break of the key contacts. When these transitions
are modelled in Maxwell's theory, one finds that, depending upon
the physical properties of the transmission line (its
resistance, inductance, capacitance, and leakage between the
conductors) different frequencies propagate
along the line at different speeds. The sharp on/off
transitions in telegraphy can be thought of,
by Fourier
transform, as the sum of a wide band of frequencies,
with the result that, when each propagates at a different
speed, a short, sharp pulse sent by the key will, at
the other end of the long line, be “smeared out”
into an extended bump with a slow rise to a peak and then
decay back to zero. Above a certain speed, adjacent dots and dashes
will run into one another and the message will be undecipherable
at the receiving end. This is why operators on the transatlantic
cables had to send at the painfully slow speed of eight words
per minute.
In telephony, it's much worse because human speech is composed
of a broad band of frequencies, and the frequencies involved
(typically up to around 3400 cycles per second) are much
higher than the off/on speeds in telegraphy. The smearing
out or dispersion as frequencies are transmitted at
different speeds results in distortion which renders the voice
signal incomprehensible beyond a certain distance.
In the mid-1850s, during development of the first transatlantic
cable, William Thomson had developed a theory called the
“KR law” which predicted the transmission speed
along a cable based upon its resistance and capacitance.
Thomson was aware that other effects existed, but without
Maxwell's theory (which would not be published in its
final form until 1873), he lacked the mathematical tools
to analyse them. The KR theory, which produced results
that predicted the behaviour of the transatlantic cable
reasonably well, held out little hope for improvement:
decreasing the resistance and capacitance of the cable would
dramatically increase its cost per unit length.
Heaviside undertook to analyse what is now called the
transmission line
problem using the full Maxwell theory and, in 1878, published
the general theory of propagation of alternating current through
transmission lines, what are now called the
telegrapher's
equations. Because he took resistance, capacitance,
inductance, and leakage all into account and thus modelled both
the electric and magnetic field created around the wire by the
changing current, he showed that by balancing these four
properties it was possible to design a transmission
line which would transmit all frequencies at the same speed. In
other words, this balanced transmission line would behave for
alternating current (including the range of frequencies in a
voice signal) just like a simple wire did for direct current:
the signal would be attenuated (reduced in amplitude) with
distance but not distorted.
In an 1887 paper, he further showed that existing telegraph
and telephone lines could be made nearly distortionless by
adding
loading coils
to increase the inductance at points along the line (as long as
the distance between adjacent coils is small compared to the
wavelength of the highest frequency carried by the line). This
got him into another battle with William Preece, whose incorrect
theory attributed distortion to inductance and advocated
minimising self-inductance in long lines. Preece moved to block
publication of Heaviside's work, with the result that the paper
on distortionless telephony, published in The
Electrician, was largely ignored. It was not until 1897
that AT&T in the United States commissioned a study of
Heaviside's work, leading to patents eventually worth millions.
The credit, and financial reward, went to Professor Michael
Pupin of Columbia University, who became another of Heaviside's
life-long enemies.
You might wonder why what seems such a simple result (which can
be written in modern notation as the equation
L/R = C/G)
which had such immediate technological utlilty eluded
so many people for so long (recall that the problem with
slow transmission on the transatlantic cable had been observed
since the 1850s). The reason is the complexity of Maxwell's
theory and the formidably difficult notation in which it
was expressed. Oliver Heaviside spent nine years
fully internalising the theory and its implications, and
he was one of only a handful of people who had done so and,
perhaps, the only one grounded in practical applications such
as telegraphy and telephony. Concurrent with his work on
transmission line theory, he invented the mathematical
field of
vector
calculus and, in 1884, reformulated Maxwell's original
theory which, written in modern notation less
cumbersome than that employed by Maxwell, looks like: