The mean value of the number of draws per hand converges to the mathematical constant e, base of the natural logarithms, approximately 2.71828….
You can observe the convergence of the mean value toward e over a large number of hands by entering the number of hands to be played in the box and pressing “Run”. The iteration count, mean value, error (absolute value of the difference between the mean value and e), and the error as a percentage of the value of e are reported for each hand up to 10, every 10 from 10 to 100, every 100 for 100 through 1000, and so on. If you request a large number of hands and/or your computer is slow, you may have to click a box warning you of an “unresponsive script” one or more times to permit the computation to run to completion. The example uses the pseudorandom number generator built into your browser's JavaScript interpreter, and will produce slightly different results every time you run it, yet the mean will invariably converge toward e.
Intuitive Exploration
Let's begin by answering the questions posed by Hints 1 and 3.
Hint 1. What is the probability distribution of the sum of a series of uniformly distributed random variables?
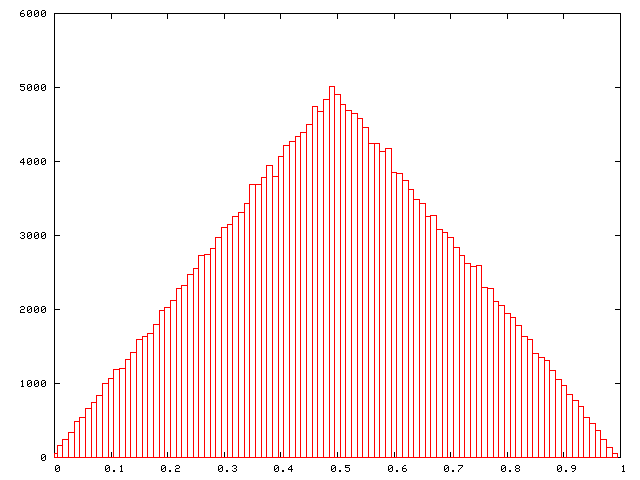
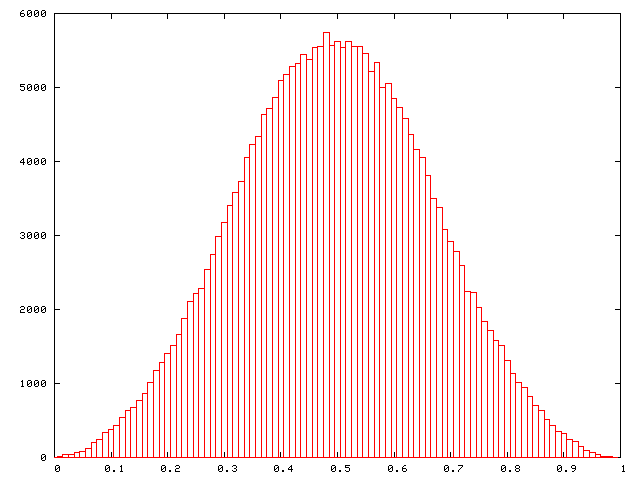
The probability distribution of the sum of a sequence of uniformly distributed random values rapidly approaches that of the normal distribution as the number of values summed increases. The following are histograms of 250,000 sums of n random values for n from 1 through 4. The sums have been normalised to the mean value is 0.5 in all the charts.
n = 1
n = 2
n = 3
n = 4
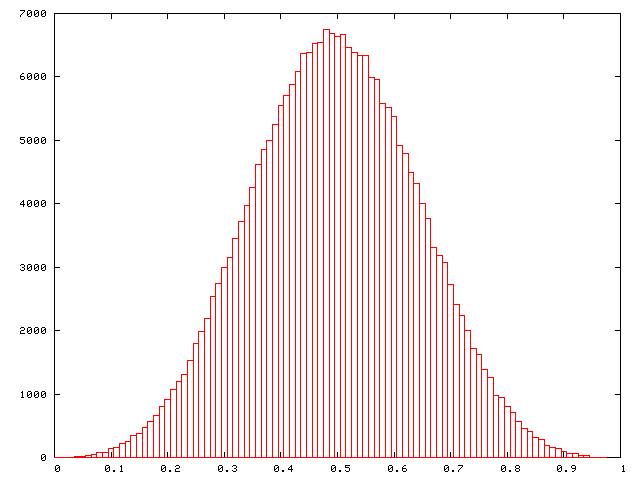
The probability density function for a variate X in a normal distribution with mean value μ and standard deviation σ is:
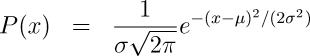
This nature of this function becomes even more clear if we assume a standard normal distribution with mean value μ=0 and standard deviation σ=1:
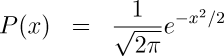
This is clearly a function in e (π appears as well, but simply as scale factor constant). Since it's unlikely in the extreme such a puzzle would have been posed had the answer not been a well-known mathematical constant, this is a compelling reason to suspect it might be e, which is further reinforced by Hint 3 below.
Hint 3. The mean value of a uniformly distributed random variable between zero and one is obviously 1/2. Why doesn't the mean number of draws then trivially converge to 2?
A naïve guess might be that the mean number of draws converges to two because the mean value of each value drawn is 1/2, and two times this value is 1. But, on further reflection, that can't possibly be right. Why? Because since the random values are always less than 1, you can never go bust on the first draw. Hence the minimum number of draws to go bust is 2. Further, it's clear that in some hands you'll have to make more than two draws before going bust, and hence the mean will have to be greater than 2. However, three times the mean value of 1/2 is 1.5, so it doesn't seem likely that the mean will be greater than three. Hence we have reason to suspect the mean is somewhere between 2 and 3. Now, what well-known constant falls between those two numbers?
Rigorous Analysis
The following discussion is based upon the analysis in Eric W. Weisstein's MathWorld page, “Uniform Sum Distribution”, expanded to show intermediate algebraic steps and explain some of the identities used.
To begin, we observe that the probability that a sum of n uniformly distributed random numbers Xn will exceed 1 while the sum of n−1 numbers will be less than or equal to 1 is:

which is simply the difference in the integrals of the probability distribution functions as plotted above for sums of n and n−1 numbers. For uniformly distributed random variates, there is a closed form solution for this integral in terms of the factorial function, so the expression may be rewritten and then algebraically simplified as follows.
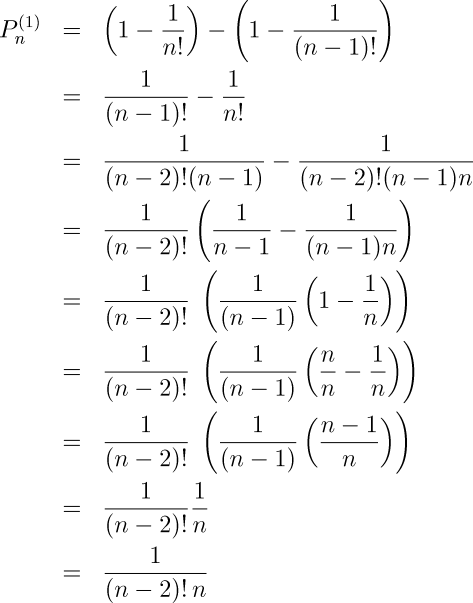
The mean number of random number draws to yield a sum which exceeds 1 may then be written as a sum of the number of draws multiplied by the probability, as determined above, of that number of draws being the one which sums to more than 1. Substituting in the expression for this probability and simplifying, we find:
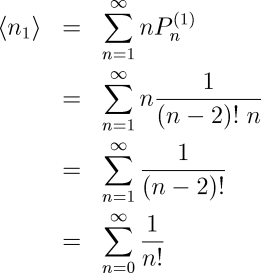
Doesn't that final series look familiar? It ought to—it's the well-known series expansion for the exponential function with an argument of 1! (If you followed the above simplification carefully, you might have noticed some fancy footwork in the last step, where a sum from 1 to infinity of 1/(n−2)! was replaced by a sum from 0 to infinity of 1/n!. You're perfectly entitled to wonder what became of the first term in this summation: 1/(−1)!. The factorial function is defined only for integers greater than or equal to zero, so in one sense this term doesn't mean anything, but a closer look provides insight into what's really going on. The Gamma function, which is the generalisation of the factorial for real and complex arguments, has a value of infinity for an argument equivalent to the factorial of −1, so the first term in the summation can be taken as 1/∞, or zero. This, in turn, simply means that since we're summing random numbers less than one, the probability of obtaining a sum greater than one by summing just one of these numbers is exactly zero. Hence the first term in the summation is zero and may be discarded by setting the start of the summation to zero.)

Hence, the mean number of random number draws to exceed 1 converges to e. If that isn't beautiful, I don't know what is.