
C-ship: The Lorentz Contraction


|
C-ship: The Lorentz Contraction |

|
An observer moving with respect to an object will observe it to be contracted along the direction of motion by the factor:
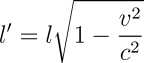
where l' is the length observed by the moving observer, l is the length measured when at rest with respect to the object, v is the velocity of the observer, and c is the speed of light. If we express v as a fraction of the speed of light, we don't have to worry about the units it's expressed in.
Then why don't people on the sidewalk look skinny when you zip past them on your bicycle? Let's look at a graph of this equation:
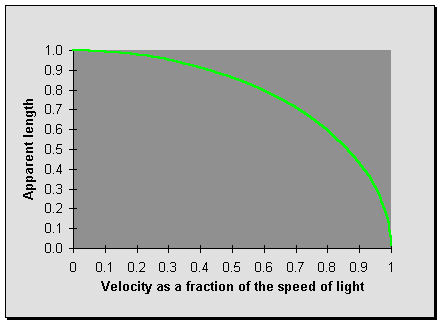
It's clear from the graph that the length contraction has little effect at small velocities, and really starts to kick in only as you approach the speed of light. Here's a table that gives the observed length for velocities of various fractions of the speed of light.
| Velocity | Observed Length |
|---|---|
| 0 | 1.000 |
| 0.1 | 0.995 |
| 0.2 | 0.980 |
| 0.3 | 0.954 |
| 0.4 | 0.917 |
| 0.5 | 0.866 |
| 0.6 | 0.800 |
| 0.7 | 0.714 |
| 0.8 | 0.600 |
| 0.9 | 0.436 |
| 0.95 | 0.312 |
| 0.97 | 0.243 |
| 0.99 | 0.141 |
| 0.995 | 0.100 |
| 0.999 | 0.045 |
| 0.9999 | 0.014 |
Now remember that the speed of light is huge compared to any velocity you encounter in everyday life; about 300,000,000 metres per second—a thousand million kilometers per hour—670 million miles an hour. When you're whizzing along on your bike at 60 km/hour, you're travelling at 0.00000005594 of the speed of light, so you observe stationary objects to be contracted by one part in 0.00000000000000155. You aren't likely to notice this; a big dog, one metre from slimy nose to smelly tail, sniffing at a fire hydrant, will appear shorter by less than the size of an atomic nucleus.
But if street peddlers don't notice the contraction, surely our exalted spacefarers must look down upon their Earthbound brethren and see us unnaturally slim! Nope. A satellite in low Earth orbit travels about 7700 metres per second, which is but 0.0000257 times the speed of light. Off-duty Blue Team gawkers putting nose-prints on the mid-deck windows of the Space Shuttle will observe objects on the Earth contracted only by a factor of 0.00000000033. Looking down upon Fourmilab from space station Mir, cosmonauts on board will see the entire 270 kilometre east to west extent of Switzerland contracted by 0.08 millimetres—20 times the size of the intestinal bacterium E. coli.
Here's a view of our ship in the foreground, stopped (at rest) with respect the the Lattice in the distant background.
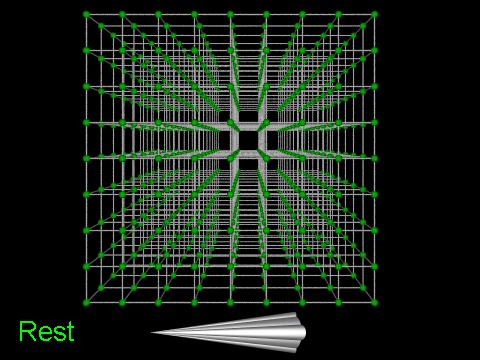
Now let's fire up the engine, accelerate to 9/10 of the speed of light, and fly by the Lattice.
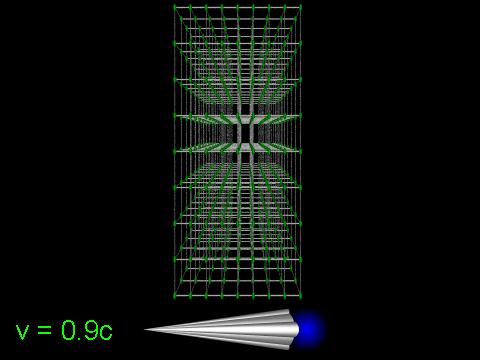
As we can see, the Lattice has shrunk to less than half its original extent in the direction we're travelling: 0.436 times to be exact.
Contraction of length occurs only along the direction of travel—note how the Lattice remains as tall and deep as before, and it depends only upon the relative motion measured by an observer. An observer stationary with respect to the Lattice would photograph (with a very fast shutter setting!) our ship flying through the lattice at 0.9c like this:

When at rest relative to the Lattice, it appears normal and the passing ship and everything on board it is contracted from the sleek shape of shipyard photos into a rather blunt instrument. Still, even though the ship is going 90% of the speed of light, it's only contracted to 43% of its length at rest. It's when we really start to pour on the antimatter and get really close to the speed of light that contraction becomes extreme. Here's a view from the same viewpoint, stationary within the Lattice, as the ship flies through at 99% of the speed of light, 0.99c.

Now we see the ship contracted to just 14% of its original length, looking more like a hubcap than a starship.
What's actually going on in the Lorentz contraction, as we'll discover a bit further down the road, is that as you approach the speed of light, you're increasingly looking at the four-dimensional fabric of space and time “edge-on”, causing space and time to mix. You can get a sense of the strangeness of this mixing by watching the following movie. The movie, like the image above, shows a view from our ship, the Lorentz, stationary with respect to the lattice, of another ship, the Minkowski, flying past us, left to right, at 99% of the speed of light. The Minkowski's engine has been turned off, so it's continuing to coast through the lattice at that speed. Using the powerful sensor array of the Lorentz, we're viewing the Minkowski from so far away she doesn't appear to move with respect to the distant lattice during the movie.
The Minkowski is conducting a survey of the Lattice, and her control computer has fired thrusters to cause the ship to pitch around an axis perpendicular to the direction of travel, allowing the sensors to sweep in a full circle. Since we observe the ship contracted along the direction of motion, the contraction results in a different apparent shape for the Minkowski as it rotates around its centre of gravity. Watching the movie may help you grasp the concept that the Lorentz contraction can be thought of as looking at a three-dimensional object from an oblique four-dimensional viewpoint.
The Lorentz contraction depends only on the relative motion of objects. An observer on board the Minkowski won't see himself and the ship flattened, he'll see the Lattice contracted along his direction of motion. Here's a movie made by the Survey Camera on board the Minkowski as she executed her pitch-around maneuver. Note how contraction occurs only in along the direction of motion. (In this movie the Survey Camera has been set to compensate for the aberration and Doppler shift, showing only the Lorentz contraction. At the velocity the Minkowski's travelling, the other effects would make the Lorentz contraction difficult to observe.)
Here's a movie from the Raw Image Camera which shows the same view, except the effects of aberration and Doppler shift are shown (the Doppler shift has been scaled to remain within the visual range).
You can also view still frames from the movie to examine them more closely.