One of the great merits of The Analytical Engine is that once a set of cards are prepared to evaluate a function, they can be used thereafter whenever that function is required in the course of subsequent calculation, simply changing the constants to whatever values are required by the new calculation. As Babbage observed in his autobiography:
Thus the Analytical Engine will possess a library of its own. Every set of cards once made will at any future time reproduce the calculations for which it was first arranged. The numerical value of its constants may then be inserted.
Without question, among the first items deposited in that library, and the most frequently used, would be sets of cards which evaluate the elementary transcendental functions of analysis: square root, logarithms, the exponential function, and the various trigonometric functions.
Our emulation of The Analytical Engine includes a modest library of cards to evaluate such functions, intended both to be used in other calculations developed for the Engine, and to illustrate how one goes about evaluating transcendental functions on the Engine. In order to understand this document, use the library functions, or examine how they are implemented, you will need to be familiar with the Programming Card notation used by the emulator.
All the library functions adhere to a consistent set of rules for passing arguments, returning results, and using columns in the Store for working variables. Once an analyst is acquainted with these rules, the various functions may be used with little thought about the details of how they are implemented.
The following sections describe each of the functions in the library. All conform to the general conventions described above for library functions. With the exception of the square root, these functions are implemented from the most straightforward series expansion, and do not range reduce their arguments or exploit symmetry. This is in keeping with the goal of demonstrating how The Analytical Engine can mechanise a mathematical process in precisely the manner it is expressed in an equation. Mathematical function libraries on modern computers generally use polynomial approximations optimised for the computer's word length. These approximations can be computed very efficiently and avoid the problem of slow convergence of some series for certain arguments and, if carefully implemented, provide accuracy within one or two bits of the word length.
Polynomial approximations, however, have inherently limited precision; if you need more decimal places, you have to find (or develop) a new approximation. Further, implementations of these approximations are intellectually opaque—they consist of lists of “magic numbers” with many decimal places (the coefficients of the polynomial) and a small sequence of code which evaluates it for the argument. A series expansion, on the other hand, translates directly from the written equation into cards for the Engine and, more importantly, can compute the value of a function to any precision whatsoever, constrained only by the fifty-digit limit on numbers in the Mill and Store. Ask the attendant to prepare up your cards to work with 30 decimal places, and the functions in this library will happily (albeit, not quickly) provide you 30 digit accuracy. Try doing that with a present-day programming language on your own computer!
The arc tangent function returns the angle, in radians, which has the tangent of the argument. The following series expansion of arctan is used.
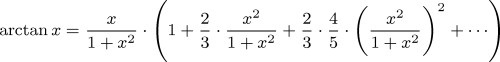
The number of terms evaluated depends upon the number of decimal places required in the result.
The cosine function returns the cosine of the argument angle, in radians. The cosine is evaluated using the following series expansion.
The exponential function returns ex for the argument x. The function is evaluated using the series:
The ln function returns the natural logarithm of its argument, calculated with the series:
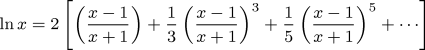
The sine function returns the sine of the argument angle, in radians. The sine is evaluated using the following series expansion.
The square root of argument N is calculated by choosing an initial guess of x0=N/2, then using the Newton-Raphson method to refine this initial value to the required precision.
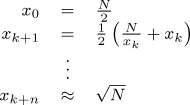
The number of iterations required depends upon the number of decimal places required; convergence is quadratic, so relatively few iterations suffice.
Since the library is primarily intended to illustrate how transcendental functions would have been computed by the Engine, it includes only the basic functions evaluated directly from series expansion or Newton's method. Other functions can be evaluated from this set of basic functions by using the mathematical identities given in the following table.
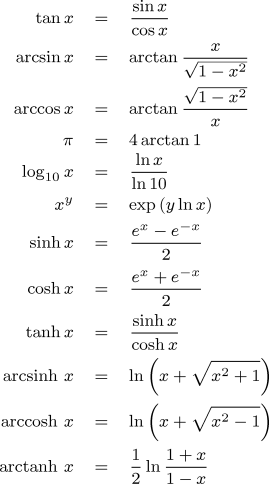
Again, function libraries for contemporary computers frequently use faster, direct polynomial approximations for some of these functions rather than the definitions above. The identities, like the functions upon which they are based, have the advantage of working regardless of the precision of the calculation.
If you run the command-line emulator on your own computer, you'll probably want to make a local copy of the mathematical function library as well. The link below downloads the library, test programs for each function, as well as the examples which follow in this document. The library is supplied as a ZIP compressed archive; when you extract the file from it, be careful to use the option which preserves directory structure, otherwise the library, test programs, and examples will all be jumbled together. You'll have to edit the file names from which the library functions are loaded to conform to the directory structure you've set up on your machine.
Download mathematical function libraryCertainly one of the first tasks to which the Analytical Engine would have applied is the computation of authoritative tables of mathematical functions. The following set of cards uses the function library to print a brief extract of a table of mathematical functions to seven decimal places, such as a Victorian engineer might have carried in his waistcoat pocket for in-the-field calculations.
x exp x ln x sin x cos x atan x sqrt x
1.0000000 2.7182818 0.0000000 0.8414710 0.5403023 0.7853982 1.0000000
1.1000000 3.0041660 0.0953102 0.8912074 0.4535961 0.8329813 1.0488088
1.2000000 3.3201169 0.1823216 0.9320391 0.3623578 0.8760581 1.0954451
1.3000000 3.6692967 0.2623643 0.9635582 0.2674988 0.9151007 1.1401754
1.4000000 4.0552000 0.3364722 0.9854497 0.1699671 0.9505468 1.1832160
1.5000000 4.4816891 0.4054651 0.9974950 0.0707372 0.9827937 1.2247449
1.6000000 4.9530324 0.4700036 0.9995736 -0.0291994 1.0121970 1.2649111
1.7000000 5.4739474 0.5306283 0.9916648 -0.1288444 1.0390723 1.3038405
1.8000000 6.0496475 0.5877867 0.9738476 -0.2272020 1.0636978 1.3416408
1.9000000 6.6858944 0.6418539 0.9463001 -0.3232895 1.0863184 1.3784049
2.0000000 7.3890561 0.6931472 0.9092974 -0.4161467 1.1071487 1.4142136
|
Click on the gears to run this example in the Web emulator.
Demonstrate mathematical function library by calculating a table of values of the various functions. V104 Iteration variable V103 Increment V101 Loop limit V105 0 V106 Current value A set decimal places to 7 A write numbers as +9.9999999 A write in columns N101 2.1 N103 0.1 N104 1.0 N105 0 A write annotation x exp x ln x sin x cos x atan x sqrt x Model output line: 1.0000000 2.7182818 0.0000000 0.8414710 0.5403023 0.7853982 1.0000000 A write new line (? + L104 L105 S000 S106 P A write annotation A include from library cards for exp + L000 P A write annotation + L106 L105 S000 A include from library cards for ln + L000 P A write annotation + L106 L105 S000 A include from library cards for sine + L000 P A write annotation + L106 L105 S000 A include from library cards for cosine +L000 P A write annotation + L106 L105 S000 A include from library cards for arctan + L000 P A write annotation + L106 L105 S000 A include from library cards for sqrt + L000 P A write annotation A write new line Update cycle variables and test for completion + L104 L103 S104 − L104 L101 )
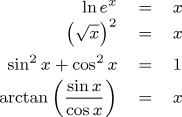This program tests the accuracy of the function library by evaluating
the mathematical identities in the equations to the right for a eleven
values of x between 0 and 1. You can change the number of
decimal places in the “A set decimal places to
35” statement near the top of the program to check accuracy
for a variety of fixed point precisions.
When run as listed below, computing to 35 decimal places, the first few
lines of output from the program are as follows.
x = 0.00000000000000000000000000000000000
ln(e(x)) = 0.00000000000000000000000000000000000
sqrt(x)² = 0.00000000000000000000000000000000000
sin²(x) + cos²(x) = 1.00000000000000000000000000000000000
arctan(sin(x) / cos(x)) = 0.00000000000000000000000000000000000
x = 0.10000000000000000000000000000000000
ln(e(x)) = 0.10000000000000000000000000000000000
sqrt(x)² = 0.09999999999999999999999999999999998
sin²(x) + cos²(x) = 0.99999999999999999999999999999999998
arctan(sin(x) / cos(x)) = 0.10000000000000000000000000000000000
x = 0.20000000000000000000000000000000000
ln(e(x)) = 0.20000000000000000000000000000000000
sqrt(x)² = 0.20000000000000000000000000000000000
sin²(x) + cos²(x) = 1.00000000000000000000000000000000000
arctan(sin(x) / cos(x)) = 0.20000000000000000000000000000000000
|
Note that even when computing results to 35 decimal places, the maximum error is ±2 in the least significant digit.
To run this example in the Web emulator, click on the gears icon to the right of the program listing.
Demonstrate mathematical function library by calculating inverses and identities of the various functions. V104 Iteration variable V103 Increment V101 Loop limit V105 0 V106 Current value A set decimal places to 35 A write numbers with decimal point A write in columns N101 1.1 N103 0.1 N104 0.0 N105 0 (? + L104 L105 S000 S106 A write annotation x = P A write new line Demonstrate ln as inverse of exp A write annotation ln(e(x)) = A include from library cards for exp A include from library cards for ln + L000 P A write new line Demonstrate square root and square as inverse A write annotation sqrt(x)² = L105 L106 S000 A include from library cards for sqrt × L000 L000 > P A write new line Demonstrate sin² x + cos² x = 1 A write annotation sin²(x) + cos²(x) = + L105 L106 S000 A include from library cards for sine ×
Click on titles to order books on-line from
|