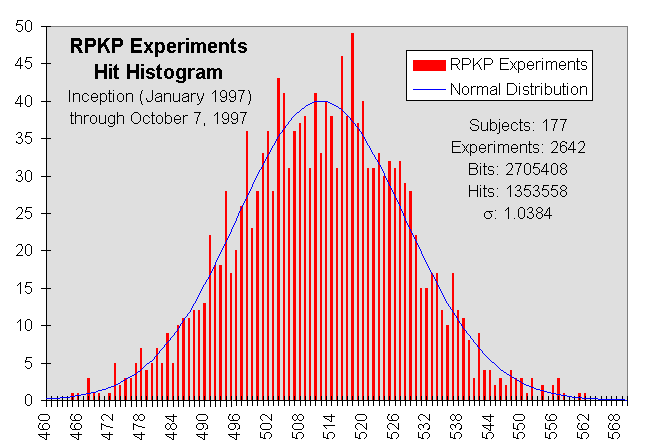
Since January of 1997, the on-line RPKP experiments have been available to anybody with Web access and a Java-equipped browser. To date, a total of 177 volunteer subjects have performed 2642 "on-the-record" experiments, the results of which are summarised below. For additional details on how the experiments are conducted, please see RPKP Update No. 8 or the RPKP Experiments home page.
During this pilot phase of RPKP experiments, no attempt was made to publicise them other than by word of mouth. Now, with nearly a year of experience to increase confidence that all is working as intended, we can now encourage those interested in experiments such as this to make links to the RPKP Home Page to invite interested volunteers to try the experiments for themselves.
Such an experiment is particularly simple to analyse with the tools of probability and statistics. For a genuinely random sequence of bits, and in the absence of anomalous sources of bias, results will converge, as more and more experiments are run, toward a binomial distribution for 1024 trials with a probability of 0.5: thus a mean value of 512 one and zero bits per experiment. Since the data and the subject's intent to bias it (toward an excess of ones or zeroes) are recorded in the log before the data are transmitted to the subject, many of the concerns about outright cheating and/or after-the-fact selection of favourable experiments can be excluded.
(Of course, this assumes the hardware random number generator I am using has no bias, the log of experiments is genuine and unexpurgated, and that no program involved contains an error which could bias the results. Finally, you're assuming I have not fabricated all of these results from whole cloth out of some obscure motive. Given the scientific and philosophical significance should consistent, statistically significant, divergences from chance emerge from such experiments, these concerns are entirely legitimate. That is why complete source code for all the programs involved has been made available for downloading, along with complete documentation on how to build a hardware random number generator identical to the one used in these experiments and the theory underlying the generator. Raw data for all experiments run to date can be downloaded by anybody, allowing them to independently verify the analysis performed by the log summary program and in status reports such as this. Further, subjects can verify that the log contains a full and accurate summary of their own experiments and, should discrepancies be found, notify all subscribers to this list by sending a message to rpkp@fourmilab.ch.)
In any case, other researchers are encouraged to replicate this experiment, ideally with a hardware random number generator based on a different technology (for example, a noise diode). All programs used in the RPKP experiments are in the public domain and may be downloaded, used, modified, and redistributed with no restrictions whatsoever.

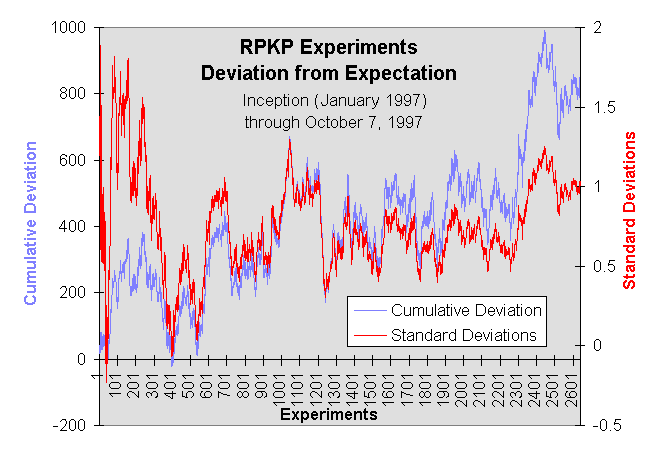
Any experiment involving a random data source can be expected to, in the absence of perturbing influences, follow a random walk around the most probable value. As the number of experiments increases, overall divergences should decrease. When examining the results of such experiments, it's important to satisfy yourself that any non-chance effect you observe doesn't result from the experimenter choosing to show you results at a peak or trough of a series which is swinging to both sides of the chance expectation with a mean value equal to chance. The following is a deviation plot of the all 2642 RPKP experiments to date; it shows the absolute divergence of the experimental results in the direction of bias preselected by the subject compared to that expected by chance, and the divergence in terms of standard deviations for the cumulative number of trials for a probability of 0.5 on each trial.
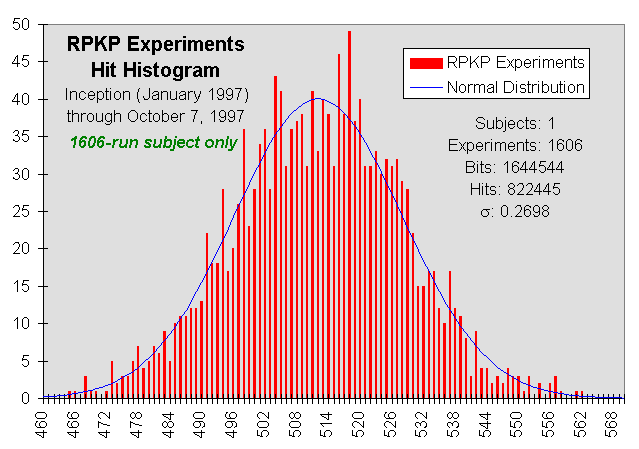
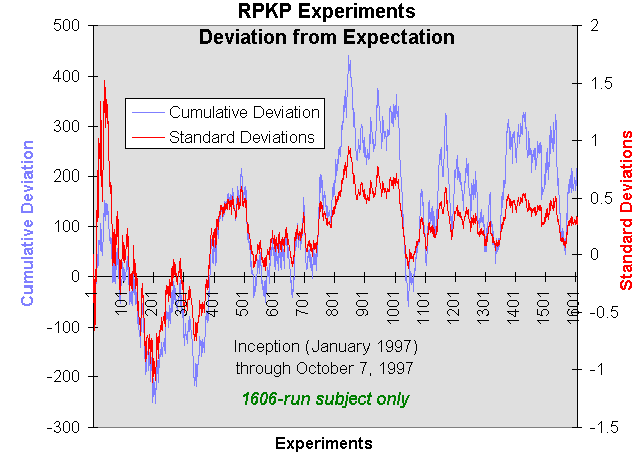
At the risk of being accused of after-the-fact data selection, results are presented below for the subject who ran the 1606 runs and for other 176 subjects together, none of whom ran more than 174 runs, and most of which did only a few experiments. I performed this analysis because the total RPKP database thus is a composite in which more than 60% of the experiments were performed by a single individual, with the balance consisting of modest number of runs by a variety of people all over the world. Analysing the data sets separately allows comparison between results obtained by a dedicated volunteer making a large number of runs over a period of many months and those of largely casual visitors who, for the most part, try only a few experiments. Here are hit histogram and deviation plots for the 1606-run subject.
| Experiments Run | Number of Subjects | Experiments Run | Number of Subjects | |
|---|---|---|---|---|
| 1 | 59 | 14 | 4 | |
| 2 | 28 | 15 | 2 | |
| 3 | 24 | 16 | 2 | |
| 4 | 13 | 17 | 1 | |
| 5 | 10 | 18 | 1 | |
| 6 | 7 | 21 | 2 | |
| 7 | 4 | 29 | 1 | |
| 8 | 3 | 30 | 1 | |
| 9 | 1 | 50 | 1 | |
| 10 | 3 | 52 | 1 | |
| 11 | 2 | 174 | 1 | |
| 12 | 3 | 1606 | 1 | |
| 13 | 2 |
The following plots are for the balance of runs, excluding those by the subject who ran the 1606 experiments. The table above gives the number of subjects who made a given number of runs.
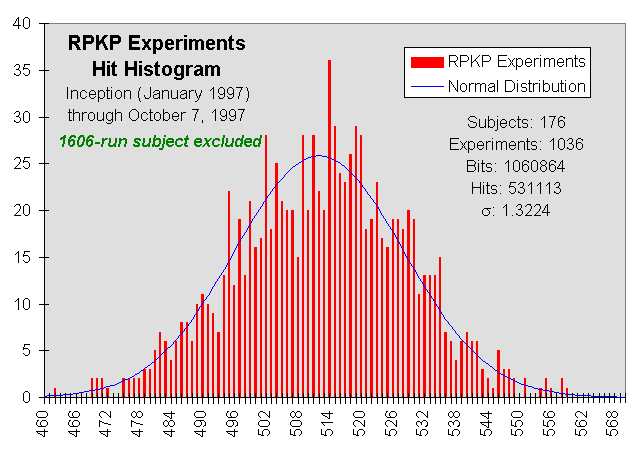
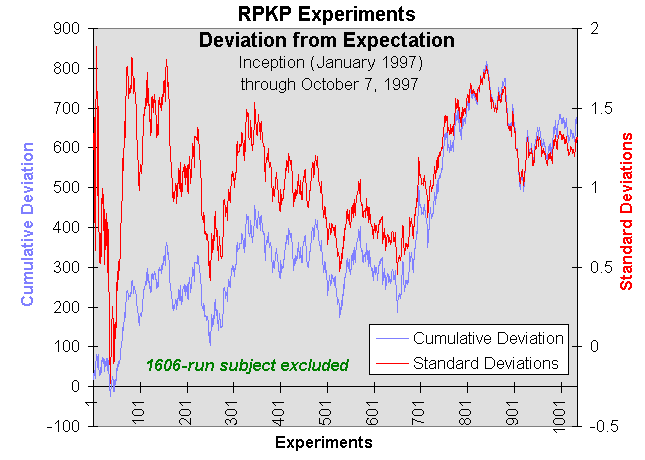
Both the composite data set and the two subsets show a bias in the direction chosen by the subject, which subjectively appears to remain as the number of experiments rises. Analysis of the log indicates that most subjects choose one bits rather than zero bits as a goal (expressed in terms of the effect on the visual feedback program: for example, the clock advancing rather than running backward). Out of a total of 2642 experiments, 2237 chose a goal of one bits, as opposed to 405 with zero bits as the objective. This might simply be due to one bits being, for each experiment, the default setting in the goal check box.
The predominant choice of one bits as a goal, combined with the bias toward the subjects' goal in the results of the 2642 experiments might, if not merely a statistical fluctuation, be due to a small excess of one bits in the output of the random number source. It is therefore worth briefly discussing why I believe no such bias exists in the HotBits generator used in these experiments. HotBits employs a Krypton-85 beta-emitting radiation source, which irradiates a Geiger-Müller tube detector interfaced to a dedicated 80486 computer. See the HotBits hardware description for additional details. To generate each bit, the intervals, timed by a software loop run with interrupts prevented on the microprocessor, between two pairs of consecutive decays are measured. Since the time of individual decays are completely uncorrelated, the relative length of the two intervals should be random, except for a tiny bias toward the second interval being longer due to the decay rate falling as fewer Krypton-85 nuclei remain in the source. This effect is negligible, as discussed in more detail in the HotBits How it Works document, being on the order of 10-14 the length of the intervals measured. Further, pairs of intervals with identical timing are discarded to avoid errors due to the measurement resolution of the computer.
As an additional precaution, and to preclude other unanticipated sources of systematic error, the sense of the comparison of the two intervals is reversed for each consecutive bit. For example, in generating bit n, we emit a zero if the first interval is longer than the second and a one otherwise, then for bit n+1 we emit a zero if the first interval is shorter and a one if it is longer. Bit n+2 flips back to the same comparison used for bit n and so on. Thus, even if there were some form of bias in the generator's measurements of the first and second intervals (and I know of neither any theoretical reason to suspect such, other than the insignificant effect of long-term decay of the sample, nor did I find any experimental evidence of bias in multi-million bit tests of the generator I performed before opening public access to it), that measurement bias would manifest itself as a bias toward ones (say) in even numbered bits in the generator output stream and an equal and opposite bias for odd numbered bits. Since every RPKP experiment uses 1024 bits from the generator, even were the generator biased, the bias would not yield a net excess of zeroes or ones, but instead a bias in even and odd bits which would cancel over an even numbered set of bits.
To reiterate, I have no reason to believe there is any significant source of bias in the output of the generator whatsoever. (The finite half-life effect is present, but not significant.) But even if there were, the swapping of the sense of comparison between bits would cancel any tendency for the mean output of the generator to diverge from the expectation of 0.5. If the deviation from expectation observed in these experiments persists and/or increases as more and more experiments are performed in the future, it will be interesting to compare the results obtained in RPKP experiments using the HotBits generator and other control tests of the output of the generator. If other sites conduct their own versions of these experiments, using different random sources, that will increase confidence that, should significant results be obtained, they do not stem from a deficiency in the random source.
 RetroPsychoKinesis Project Home
RetroPsychoKinesis Project Home