Exponentially smoothed moving averages

Next: Calculating best fit Up: Calculating moving averages Previous: Weighted moving averages

Exponentially smoothed moving averages

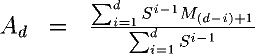
An exponentially smoothed moving average is a weighted moving average in which the weight factors are powers of S, the smoothing constant. An exponentially smoothed moving average is computed over all the data accumulated so far instead of being chopped off after some number of days. For day d the exponentially smoothed moving average is:

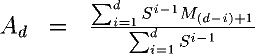
$A_d = \frac{\sum_{i=1}^{d} S^{i-1} M_{(d-i)+1}}{\sum_{i=1}^{d} S^{i-1}}$

But this is just a geometric sequence! The next term in such a sequence is given by: A_d=(1-S)M_d+SA_d-1. Calculation is expedited and comprehension served if we substitute: P=1-S for S into the equation for the next term. Doing a little algebra, we discover:

A[d] = A[d - 1] + P (M[d] - A[d - 1])

This reformulation makes the operation of smoothing very intuitive. Every day, we take the old trend number A_d-1, calculate the difference between it and today's measurement M_d, then add a percentage of that difference P to the old trend value obtain the new one. Obviously, the closer P is to 1 (and hence the closer S is to zero), the more influence the new measurement has upon the trend. If P=1, the old trend value A_d-1 cancels out and the moving average tracks the data precisely.

For example, with the smoothing constant S=0.9 we use on weight data, we calculate the new trend value A_d from the previous trend value A_d-1 and today's weight M_d as:

A[d] = A[d - 1] + 0.1 (M[d] - A[d - 1])

In discussions of exponentially smoothed moving averages, particularly their financial applications, beware of confusing the smoothing constant S with the variant form P=1-S introduced to simplify calculation and make the effect of the new data on the moving average more apparent. P is often referred to as the ``smoothing percentage''; the term ``10% smoothing'' refers to a calculation in which P=10/100=0.1 and hence S=0.9.

By John Walker