

One of my favourite science fiction stories is Larry Niven's Inconstant Moon, about a night when the full Moon shone brighter than ever before. I won't say any more about the story so as not to spoil it for those who have yet to discover this most atypical gem in Niven's vast treasure chest. Find it; read it; enjoy!
Everybody notices the phases of the Moon, but to most people every full Moon is alike—the rising or setting Moon looks large due to perspective's playing tricks on the eye, but surely the full Moon high in the sky is always the same, right? Wrong.
One of the most spectacular phenomena in naked-eye astronomy escapes notice by the vast majority of people simply because the the eye and brain can't compare the size and brightness of objects observed on separate occasions. This page explores the inconstant Moon in our everyday sky. While not as dramatic as that conjured up by the imagination of Larry Niven, we'll discover in it a celestial phenomenon seen by everybody, yet observed by only a few individuals.
The Moon's orbit around the Earth is elliptical, with a substantial eccentricity (as major Solar System bodies go) of 5.49%. In addition, the tidal effect of the Sun's gravitational field increases the eccentricity when the orbit's major axis is aligned with the Sun-Earth vector or, in other words, the Moon is full or new.
The combined effects of orbital eccentricity and the Sun's tides result in a substantial difference in the apparent size and brightness of the Moon at perigee and apogee. Extreme values for perigee and apogee distance occur when perigee or apogee passage occurs close to new or full Moon, and long-term extremes are in the months near to Earth's perihelion passage (closest approach to the Sun, when the Sun's tidal effects are strongest) in the first few days of January.
The image above shows how strikingly different the Moon appears at a full-Moon perigee and apogee. Most people don't notice the difference because they see the Moon in a sky that offers no reference by which angular extent may be judged. To observe the difference, you have to either make a scale to measure the Moon, or else photograph the Moon at perigee and apogee and compare the pictures, as I've done here.
The following table shows larger images of perigean and apogean full Moons, with details of the position of the Moon at the moment the pictures were taken. If your screen can't display the images one above another, use the side by side image above to appreciate the difference in size.
Since we can determine the position of the Moon at the time the exposures were made, it's possible to verify whether the resulting images agree with our calculations. To do this, we first measure the size of the Moon's disc in the perigee and apogee images, then compute the size ratio. This should agree, within the accuracy of the measurement, with the ratio of angular sizes computed from the distance of the Moon when the respective photos were shot.
To avoid errors due to the Moon's not being perfectly full in either of the images, we'll measure the vertical extent of the disc, which is fully illuminated. Due to its inherent roughness, resolution limits of the optics and film, and distortion caused by turbulence in the Earth's atmosphere (“seeing”), the Moon's limb is not perfectly sharp in these pictures, so some judgement enters into the measuring process. Trying to use a consistent ratio of brightness on the two images, I measure the Moon in the perigee image to be 363 pixels high and the Moon at apogee to be 323 pixels, yielding a perigee/apogee ratio of 1.1238. I believe these size estimates are correct within ±1 pixel, giving tolerance limits on the ratio of 1.1173 to 1.1304.
For sufficiently small angles, the sine of an angle is approximated closely by the angle in radians. The Moon's angular extent viewed from Earth is small enough that this approximation is adequate for this calculation, so we can simply use the ratio of viewing distances as a proxy for the Moon's angular size. Dividing the apogee distance by that of the perigee gives 405948/359861 = 1.1281, in close agreement with the ratio of image sizes.
But we can do better than this: the perigee and apogee distances are calculated based on the distance between the centres of the Earth and Moon. Now from any sufficiently distant viewpoint the distance to the Moon's limb is essentially the same as that to its centre, but an observer on the surface of the Earth is necessarily closer to the Moon than the centre of the Earth. While the Earth's surface is not an ideal place to do astronomy, it sure beats setting up your telescope at the Earth's core, where 6378 km of rock attenuates even the brightest moonlight something terrible! So, what we're really interested in is not how far the Moon was from the centre of the Earth (its geocentric coordinates), but how far it was from the telescope when each picture was made. This is not an insignificant consideration: an observer at the equator observing the Moon at zenith is 1.8% closer to the Moon's limb than an observer 90° east or west in longitude, watching the Moon set or rise at the same moment.
What we want, then, is the position of the Moon relative to the observer, its topographic coordinates for the observing site. An easy way to calculate this is to transform the Moon's position in the spherical geocentric coordinate system into rectangular (Cartesian, or XYZ) coordinates with the origin at the centre of the Earth. The observer's position in the same coordinate system is easily calculated from the latitude and longitude of the observing site and, if you want to be as precise as possible, the distance from the centre of the Earth to the observing site, taking into account the Earth's ellipsoidal shape and the site's altitude above mean sea level. Then the distance from the observer, (XO, YO, ZO), to the Moon, (XM, YM, ZM), can be calculated with the distance formula for rectangular coordinates:
![]()
This calculation gives an observer to Moon's limb distance of 404510 kilometres for the apogee image and 359000 km for the perigee image, with a perigee to apogee ratio of 1.1268, even closer to the best estimate of the image size ratio, 1.1238.
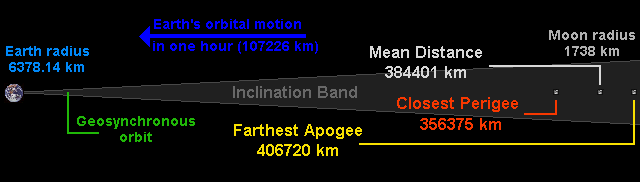
The Earth-Moon System to Scale,
650 km/pixel
Space is called “space” because there's so much space there. Astronauts who flew to the Moon were struck by how the Earth and Moon seemed tiny specks in an infinite, empty void. So large are the voids that separate celestial bodies that most illustrations exaggerate the size of the objects to avoid rendering them as invisible dots. Compared to most other moons in the Solar System (Pluto's moon Charon is a notable exception), the Earth's Moon is very large compared to the planet it orbits, so it is possible, just barely, to draw the Earth-Moon system to scale in a form that will fit on a typical computer screen. The image above shows the Earth at the left and the Moon at the right, as they would appear to an observer looking from the direction of the Sun when the Moon is at first quarter; both worlds are fully illuminated (as is always the case when viewing from sunward, of course), and the Moon is at its maximum elongation from the Earth. Earth's orbital motion is toward the left, with the arrow at the top showing how far the Earth and Moon travel along their common orbit about the Sun every hour.
On this scale, all human spaceflight with the exception of the Apollo lunar missions has been confined to a region of two pixels surrounding the Earth; seeing the Moon's orbit in its true scale brings home how extraordinary an undertaking the Apollo project was. Of all the human beings who have lived on Earth since the origin of our species, only 24 have ventured outside that thin shell surrounding our Home Planet. Even the orbit which geosynchronous communications satellites occupy is only a little more than a tenth of the way to the Moon.
The mean distance to the moon, 384401 km, is the semimajor axis of its elliptical orbit. The closest perigee in the years 1750 through 2125 was 356375 km on 4th January 1912; the most distant apogee in the same period will be 406720 km on 3rd February 2125 (have your camera ready!). These extrema are marked on the chart, although in reality extreme perigees and apogees always occur close to a new or full Moon, not at a quarter phase as illustrated here. The mean distance is not equidistant between the minimum and maximum because the Sun's gravity perturbs the orbit away from a true ellipse. Although the absolute extremes are separated by many years, almost every year has a perigee and apogee close enough to the absolute limits to be indistinguishable at this scale.
The Moon's orbit is inclined 5.145396° with regard to the ecliptic (the plane in which the Earth's orbit around the Sun lies or, more precisely, the plane in which the centre of gravity of the Earth-Moon system [its barycentre] orbits the Sun), so as seen from the centre of the Earth the Moon drifts up and down slightly more than five degrees in the course of each orbit. The dark grey wedge shows the limits of the Moon's excursion above and below the plane of the ecliptic.
The Moon's orbital inclination, combined with the inclination of the Earth's axis of rotation, causes the Moon's declination, as observed from the Earth, to vary between ±28.5° when the Moon's inclination adds to that of the Earth, and ±18° when the two inclinations oppose one another; the maxima and minima of declination repeat every 18.6 years, the period in which the ascending node of the Moon's orbit precesses through a full circle.
When the Moon is full near perigee, you'd expect it to be brighter than a full Moon near apogee and it is: lots brighter; let's figure out how much. Since the Moon shines by reflecting sunlight (not very well—it reflects only about 7% of the light that strikes it, comparable to a lump of coal) the following two factors determine the intensity of moonlight at the Earth:
Since the difference between the minimum and maximum distance of the Moon, 50345 km, is an insignificant fraction of the average distance from the Sun to the Earth and Moon, 149597870 km, the intensity of sunlight at the Moon can be considered constant and ignored in this calculation. (Sunlight intensity at the Moon does vary, of course, due to the eccentricity of the Earth's orbit around the Sun, but we'll ignore that smaller annual effect here since we're concentrating on lunar perigee and apogee.)
The intensity of light varies as the inverse square of the distance between a light source and the observer, so taking the ratio between the perigee and apogee distances in the photographs above as typical, the distance at apogee was 1.1363 times the perigee distance, and hence the Moon's intensity at perigee was the square of this quantity, 1.2912 times brighter—about 30%. Using the long-term extremes plotted in the drawing in the previous section yields only a slightly greater intensity difference: a distance variation of 1.1413, with the Moon shining 1.3026 times brighter at perigee.
Like the variation in angular size, few people ever notice this substantial difference in the intensity of moonlight at perigee and apogee because there's no absolute reference against which to compare them. If you could flick a switch and move the Moon back and forth between apogee and perigee, the difference would be obvious, though not as evident as you might expect from a 30% change in illumination due to the logarithmic response of the human eye. Another document on this site discusses the differences between the linear response of photographic film and electronic sensors as opposed to the human eye, and how computer image processing techniques can allow producing images that approximate visual perception.
An interesting project would be to photograph the same landscape with identical film, lens, and exposure at lunar perigee and apogee and compare the resulting images. If you're interested in doing this with conventional film photography, be sure to use reversal transparency (colour slide) film rather than negative print film. Unless you have control of the entire process of development and printing, the automatic balancing done by photo labs, combined with the great latitude of print film, intended to compensate for non-optimal exposures, will hide the difference in illumination. With slide film, the negative directly reflects the light intensity of the exposure and should show the difference between moonlight at perigee and apogee. If you undertake this experiment, concentrate on making the exposures as close as possible to the same interval before or after the full Moon as opposed to aiming for the precise moment of perigee or apogee. The Moon brightens dramatically when full—it is more than twice as bright at the moment of fullness than only 2½ days before or afterward. A slight difference in phase can swamp the more subtle and slowly changing brightness due to the Moon's distance, yielding misleading results.
 You may have noticed while examining the pictures above that the
two images of the Moon differ not only in size, but in the
position of features on the disc of the Moon. This might seem
puzzling in light of the frequently-stated assertion “the
Moon always keeps the same face toward the Earth”. But
this generalisation is not strictly true; in fact, the
combination of the eccentricity and inclination of the Moon's
orbit causes the Moon, as seen from the Earth, to nod up and
down and left and right. These apparent motions, the lunar
librations, allow us to observe, over a period of time,
more than 59% of the Moon's surface from the Earth, albeit with
the terrain in the libration zones near the edge of the
visible disc, only very obliquely.
You may have noticed while examining the pictures above that the
two images of the Moon differ not only in size, but in the
position of features on the disc of the Moon. This might seem
puzzling in light of the frequently-stated assertion “the
Moon always keeps the same face toward the Earth”. But
this generalisation is not strictly true; in fact, the
combination of the eccentricity and inclination of the Moon's
orbit causes the Moon, as seen from the Earth, to nod up and
down and left and right. These apparent motions, the lunar
librations, allow us to observe, over a period of time,
more than 59% of the Moon's surface from the Earth, albeit with
the terrain in the libration zones near the edge of the
visible disc, only very obliquely.
In the image at left, I've rescaled the perigee and apogee images so both are the same size, and combined them into an image which blinks back and forth for easier comparison. (If the image doesn't blink, your Web browser doesn't support GIF animations; click on the image to view a side-by-side image for comparison, then use your browser's “Back” button to return here. If the blinking image annoys you, your browser's “Stop” button should make it stop blinking.)
As the image blinks from the apogee to perigee view, the Moon
appears to rotate around Mare Crisium, the dark
circle near the upper right (northeast) limb of the Moon. To
understand the difference in the appearance of the Moon in these
two images, consider the position of the Moon with respect to
the Earth as shown in the following charts prepared with
Home Planet. You can produce your own
custom sky maps and horizon images on the Web with our
Your Sky page.
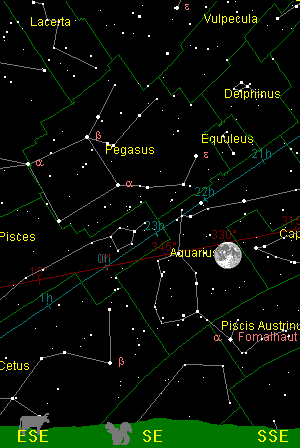
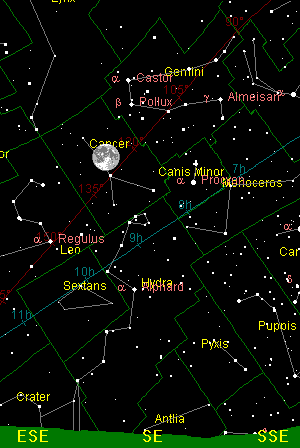
| Perigee: 1987 August 10 | Apogee: 1988 February 2 |
|---|---|
 |
 |
The light blue line is the celestial equator, the projection of the Earth's equator onto the sky. The red line marks the ecliptic, the plane in which the Earth orbits the Sun. At the time the perigee picture was taken, the Moon was south of the ecliptic due to its position along its inclined orbit, and as a result, observers on Earth at that time were looking down onto the Moon's north pole, with the Moon's equator appearing below the middle of the visible disc. Since the Moon was, at that moment, south of the equator as seen from Earth, an observer in the northern hemisphere was additionally displaced northward and could see farther past the north pole of the Moon.
At the time of the apogee photo, the situation was the opposite; the Moon was both above the ecliptic and 22½° north of the celestial equator. Consequently, observers on Earth saw the south pole of the Moon tilted toward them, with the lunar equator displaced toward the northern limb of the Moon.
In addition to the north-south displacement due to the inclination of the Moon's orbit, the eccentricity of the Moon's orbit creates an east-west displacement. The rate at which a massive solid body such as the Moon rotates with respect to the distant stars is, for all practical purposes, constant. Since the Moon's is tidally locked to the Earth, it rotates on its axis in a time equal to the time in which it completes an orbit around the Earth. Observers on Earth view the Moon not from the centre of a circle, however, but from a focus of its elliptical orbit. When the Moon is closer to the Earth, around perigee, its orbital motion is faster and carries it past the Earth faster than its constant rotation speed. When the Moon is near apogee, its slower orbital motion causes the rotation to get ahead of the orbital motion, revealing terrain on the other side of the mean limb.
The bright crater Tycho near the southern limb of the Moon makes a convenient marker; notice how much more terrain to the south of that crater is visible in the apogee image.
Finally, the difference in the illumination of the Moon is due to the perigee picture's being taken almost a day after full Moon, as compared to the apogee picture, exposed 15 hours before the Moon was full. Practical considerations such as the Moon's position in the sky, the time of sunset and sunrise, and the need for clear skies usually require compromises which prevent capturing the Moon at precisely the moment it is full. The brightness of the Moon varies dramatically around the time of full Moon; as is evident from these pictures, the difference in appearance less than a day on either side of full is readily perceptible.
If you're interested in making your own photographs of the Moon at perigee and apogee, or just observing the Moon visually, perhaps with a ruler held at arm's length to gauge its angular size, visit our Lunar Perigee and Apogee Calculator which, assuming your Web brower supports JavaScript, will prepare a list of closest perigees and farthest apogees for any given year, along with the interval separating each perigee or apogee from the nearest new or full Moon.
As with most projects in amateur astronomy, unless you're a full-on fanatic (you know, the kind who would go all the way to Australia to get a glimpse of Halley's Comet near perihelion—gosh it was hot and dry out there in the outback!) you have to compromise between the ideal situation and the constraints of real-world observing conditions. Our calculator will show you the various photo opportunities available in the coming months and years; you'll notice that more apogees occur close to extreme distances than perigees. If you want to make perigee and apogee pictures which are easily compared, you're better off choosing perigees and apogees as close as possible to full Moon (or close to the same time before or after full phase) rather than focusing on the moment of perigee or apogee with substantially different phase; as you can see from the pictures above, even over a relatively small interval around full Moon the appearance of the Moon changes noticeably, which may obscure, in part, the essential difference between perigee and apogee.
Never trust the weather forecast! If it's clear the night before the optimal full Moon at perigee or apogee, take some “just in case” shots so you don't come up empty-handed if the fog rolls in or a thunderstorm brews up before sunset on the night you planned to photograph the Moon. The images in this document are, in fact, all “contingency samples”, made in one case the night before fog wiped out my planned observing session and, in the other, the night after.
 All photographs were made with a VERNONscope Brandon 80 mm
apochromatic refractor and a Nikkormat camera body. Perigee
exposures were made on Kodak Tri-X (ASA 400, emulsion TX5063)
film, and apogee exposures on Kodak Plus-X (ASA 100, emulsion
PX5062) film; both black and white negative films. Exposure
times were bracketed over a wide range and the best chosen by
examination of the negatives; no record of exposure time was
made. The slower Plus-X film was chosen for the apogee
exposures after examination of the perigee film showed that only
the shortest exposures yielded usable negatives.
All photographs were made with a VERNONscope Brandon 80 mm
apochromatic refractor and a Nikkormat camera body. Perigee
exposures were made on Kodak Tri-X (ASA 400, emulsion TX5063)
film, and apogee exposures on Kodak Plus-X (ASA 100, emulsion
PX5062) film; both black and white negative films. Exposure
times were bracketed over a wide range and the best chosen by
examination of the negatives; no record of exposure time was
made. The slower Plus-X film was chosen for the apogee
exposures after examination of the perigee film showed that only
the shortest exposures yielded usable negatives.
The best negatives, chosen by examination under a magnifier on a
light table, were transferred to a Kodak Photo CD, from which
the images were viewed with the imgview utility on a
Silicon Graphics Indigo² workstation. Selected images were then
extracted into bitmaps at “Level 4” (1536×1024
pixel) resolution. The contrast and brightness of the images
were adjusted to facilitate comparison and improve appearance on
computer displays limited to 256 shades of grey, and the apogee
image was passed through a moderate high-pass sharpening filter
to enhance detail in the smaller image. The images were not
adjusted in scale: they correspond pixel-by-pixel to the
contents of the original negatives. All image size measurements
were made on the original, unprocessed images, viewed directly
from the Photo CD.
Using a Photo CD to transfer the images from the original negatives to the computer preserves far more of the light intensity range than making a print from the negative and scanning it. In addition, you're guaranteed the negatives will be transferred with a uniform scale. If you have prints made by a commercial lab, you may discover, especially if they're done months apart as is often the case when chasing perigees and apogees, that the negatives have been printed at sufficiently different magnifications as to render comparison impossible. Unless you make the enlargements yourself with uniform magnification, there's no way to be absolutely sure the image size on the prints corresponds to the scale of the image on the negative. The automated scanning process used to create a Photo CD guarantees identical scale, especially if you have all the negatives scanned in one batch.
|
Click on titles to order books on-line from
|
Lunar Perigee and Apogee Calculator
Moon near Perigee, Earth near Aphelion
Return to Earth and Moon Viewer
Your Sky
Other Astronomy and Space resources at this site
|
|
May, 1997
This document and all the images it contains are in the public domain.