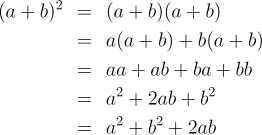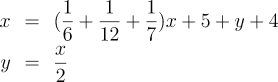- Farmelo, Graham.
The Strangest Man.
New York: Basic Books, 2009.
ISBN 978-0-465-02210-6.
-
Paul Adrien Maurice Dirac was born in 1902 in Bristol, England. His father,
Charles, was a Swiss-French immigrant who made his living as a French teacher at a
local school and as a private tutor in French. His mother, Florence (Flo), had
given up her job as a librarian upon marrying Charles. The young Paul and his
older brother Felix found themselves growing up in a very unusual, verging upon
bizarre, home environment. Their father was as strict a disciplinarian at home
as in the schoolroom, and spoke only French to his children, requiring them to
answer in that language and abruptly correcting them if they committed any
faute de français. Flo spoke to the
children only in English, and since the Diracs rarely received visitors at home,
before going to school Paul got the idea that men and women spoke different
languages. At dinner time Charles and Paul would eat in the dining room,
speaking French exclusively (with any error swiftly chastised) while Flo,
Felix, and younger daughter Betty ate in the kitchen, speaking English.
Paul quickly learned that the less he said, the fewer opportunities for error
and humiliation, and he traced his famous reputation for taciturnity to his
childhood experience.
(It should be noted that the only account we have of Dirac's childhood
experience comes from himself, much later in life. He made no attempt to
conceal the extent he despised his father [who was respected by his
colleagues and acquaintances in Bristol], and there is no way to know
whether Paul exaggerated or embroidered upon the circumstances of his
childhood.)
After a primary education in which he was regarded as a sound but
not exceptional pupil, Paul followed his brother Felix into the
Merchant Venturers' School, a Bristol technical school ranked
among the finest in the country. There he quickly distinguished
himself, ranking near the top in most subjects. The instruction
was intensely practical, eschewing Latin, Greek, and music in favour
of mathematics, science, geometric and mechanical drawing, and
practical skills such as operating machine tools. Dirac learned
physics and mathematics with the engineer's eye to “getting the
answer out” as opposed to finding the most elegant solution
to the problem. He then pursued his engineering studies at
Bristol University, where he excelled in mathematics but struggled
with experiments.
Dirac graduated with a first-class honours degree in engineering, only
to find the British economy in a terrible post-war depression, the
worst economic downturn since the start of the Industrial Revolution.
Unable to find employment as an engineer, he returned to Bristol University
to do a second degree in mathematics, where it was arranged he could skip
the first year of the program and pay no tuition fees. Dirac quickly
established himself as the star of the mathematics programme, and also
attended lectures about the enigmatic quantum theory.
His father had been working in the background to secure a position at
Cambridge for Paul, and after cobbling together scholarships and a
gift from his father, Dirac arrived at the university in October 1923
to pursue a doctorate in theoretical physics. Dirac would already have seemed
strange to his fellow students. While most were scions of the upper
class, classically trained, with plummy accents, Dirac knew no Latin or
Greek, spoke with a Bristol accent, and approached problems as an
engineer or mathematician, not a physicist. He had hoped to study
Einstein's general relativity, the discovery of which had first interested
him in theoretical physics, but his supervisor was interested in
quantum mechanics and directed his work into that field.
It was an auspicious time for a talented researcher to undertake
work in quantum theory. The “old quantum theory”,
elaborated in the early years of the 20th century, had explained
puzzles like the distribution of energy in heat radiation and the
photoelectric effect, but by the 1920s it was clear that nature
was much more subtle. For example, the original quantum theory failed
to explain even the spectral lines of hydrogen, the simplest atom.
Dirac began working on modest questions related to quantum theory, but
his life was changed when he read
Heisenberg's 1925 paper which is now
considered one of the pillars of the new quantum mechanics. After
initially dismissing the paper as overly complicated and artificial,
he came to believe that it pointed the way forward, dismissing Bohr's
concept of atoms like little solar systems in favour of a probability
density function which gives the probability an electron will be observed
in a given position. This represented not just a change in the model
of the atom but the discarding entirely of models in favour of a
mathematical formulation which permitted calculating what could be
observed without providing any mechanism whatsoever explaining how it worked.
After reading and fully appreciating the significance of Heisenberg's work,
Dirac embarked on one of the most productive bursts of discovery in
the history of modern physics. Between 1925 and 1933 he published one
foundational paper after another. His Ph.D. in 1926, the first granted
by Cambridge for work in quantum mechanics, linked Heisenberg's theory to
the classical mechanics he had learned as an engineer and provided a framework
which made Heisenberg's work more accessible. Scholarly writing did not
come easily to Dirac, but he mastered the art to such an extent that his
papers are still read today as examples of pellucid exposition. At
a time when many contributions to quantum mechanics were rough-edged
and difficult to understand even by specialists, Dirac's papers were, in
the words of Freeman Dyson, “like exquisitely carved marble statues
falling out of the sky, one after another.”
In 1928, Dirac took the first step to unify quantum mechanics and special
relativity in the
Dirac equation.
The consequences of this equation led Dirac to predict the existence
of a positively-charged electron, which had never been observed. This
was the first time a theoretical physicist had predicted the existence of a
new particle. This
“positron”
was observed in debris from
cosmic ray collisions in 1932. The Dirac equation also interpreted the
spin
(angular momentum) of particles as a relativistic phenomenon.
Dirac, along with Enrico Fermi, elaborated the statistics of particles
with half-integral spin (now called
“fermions”).
The behaviour
of ensembles of one such particle, the electron, is essential to the devices
you use to read this article. He took the first steps toward a relativistic
theory of light and matter and coined the name,
“quantum electrodynamics”,
for the field, but never found a theory sufficiently simple and beautiful
to satisfy himself. He published
The Principles of Quantum Mechanics
in 1930, for many years the standard textbook on the subject and still read
today. He worked out the theory of
magnetic monopoles
(not detected to
this date) and speculated on the origin and possible links between
large
numbers in physics and cosmology.
The significance of Dirac's work was recognised at the time. He was elected
a Fellow of the
Royal Society in 1930,
became the Lucasian Professor of
Mathematics (Newton's chair) at Cambridge in 1932, and shared the Nobel
Prize in Physics for 1933 with Erwin Schrödinger. After rejecting
a knighthood because he disliked being addressed by his first name, he was
awarded the
Order of Merit in 1973. He is commemorated by a plaque in
Westminster Abbey, close to that of Newton; the plaque bears his name and
the Dirac equation, the only equation so honoured.
Many physicists consider Dirac the second greatest theoretical physicist of the
20th century, after Einstein. While Einstein produced great leaps of intellectual
achievement in fields neglected by others, Dirac, working alone, contributed
to the grand edifice of quantum mechanics, which occupied many of the
most talented theorists of a generation. You have to dig a bit deeper into the
history of quantum mechanics to fully appreciate Dirac's achievement, which
probably accounts for his name not being as well known as it deserves.
There is much more to Dirac, all described in this extensively-documented scientific
biography. While declining to join the British atomic weapons project during
World War II because he refused to work as part of a collaboration, he spent
much of the war doing consulting work for the project on his own, including
inventing a new technique for isotope separation. (Dirac's process proved less
efficient that those eventually chosen by the Manhattan project and was not
used.) As an extreme introvert, nobody expected him to ever marry, and he
astonished even his closest associates when he married the sister of his
fellow physicist Eugene Wigner, Manci, a Hungarian divorcée with two
children by her first husband. Manci was as extroverted as Dirac was reserved,
and their marriage in 1937 lasted until Dirac's death in 1984. They had two
daughters together, and lived a remarkably normal family life. Dirac, who
disdained philosophy in his early years, became intensely interested in the
philosophy of science later in life, even arguing that mathematical beauty,
not experimental results, could best guide theorists to the best expression
of the laws of nature.
Paul Dirac was a very complicated man, and this is a complicated and occasionally
self-contradictory biography (but the contradiction is in the subject's life,
not the fault of the biographer). This book provides a glimpse of a unique
intellect whom even many of his closest associates never really felt they
completely knew.

- Mazur, Joseph.
Enlightening Symbols.
Princeton: Princeton University Press, 2014.
ISBN 978-0-691-15463-3.
-
Sometimes an invention is so profound and significant yet apparently
obvious in retrospect that it is difficult to imagine how people
around the world struggled over millennia to discover it, and how
slowly it was to diffuse from its points of origin into general use.
Such is the case for our modern decimal system of positional
notation for numbers and the notation for algebra and other
fields of mathematics which permits rapid calculation and
transformation of expressions. This book, written with the extensive source citations
of a scholarly work yet accessible to any reader familiar with
arithmetic and basic algebra, traces the often murky origins of
this essential part of our intellectual heritage.
From prehistoric times humans have had the need to count things,
for example, the number of sheep in a field. This could be
done by establishing a one-to-one correspondence between the
sheep and something else more portable such as
one's fingers (for a small flock), or pebbles kept in a sack.
To determine whether a sheep was missing, just remove a
pebble for each sheep and if any remained in the sack,
that indicates how many are absent. At a slightly more abstract
level, one could make tally marks on a piece of bark or clay
tablet, one for each sheep. But all of this does not imply
number as an abstraction independent of individual items of
some kind or another. Ancestral humans don't seem to have
required more than the simplest notion of numbers: until the
middle of the 20th century several tribes of Australian
aborigines had no words for numbers in their languages at all,
but counted things by making marks in the sand. Anthropologists
discovered tribes in remote areas of the Americas, Pacific
Islands, and Australia whose languages had no words for numbers
greater than four.
With the emergence of settled human populations and the
increasingly complex interactions of trade between villages
and eventually cities, a more sophisticated notion of numbers
was required. A merchant might need to compute how many
kinds of one good to exchange for another and to keep records
of his inventory of various items. The earliest known
written records of numerical writing are Sumerian cuneiform clay
tablets dating from around 3400 B.C.
These tablets show number symbols formed from two distinct
kinds of marks pressed into wet clay with a stylus. While
the smaller numbers seem clearly evolved from tally marks,
larger numbers are formed by complicated combinations of the
two symbols representing numbers from 1 to 59. Larger numbers
were written as groups of powers of 60 separated by spaces.
This was the first known instance of a positional number system,
but there is no evidence it was used for complicated calculations—just
as a means of recording quantities.
Ancient civilisations: Egypt, Hebrew, Greece, China, Rome, and the
Aztecs and Mayas in the Western Hemisphere all invented
ways of writing numbers, some sophisticated and capable of
representing large quantities. Many of these systems were
additive: they used symbols, sometimes derived from
letters in their alphabets, and composed numbers by writing
symbols which summed to the total. To write the number 563,
a Greek would write
“φξγ”,
where φ=500,
ξ=60, and
γ=3. By convention, numbers were
written with letters in descending order of the value they
represented, but the system was not positional. This made
the system clumsy for representing large numbers, reusing
letters with accent marks to represent thousands and an
entirely different convention for ten thousands.
How did such advanced civilisations get along using number systems
in which it is almost impossible to compute? Just imagine a
Roman faced with multiplying MDXLIX by XLVII
(1549 × 47)—where do you start?
You don't: all of these civilisations used some form of
mechanical computational aid: an abacus, counting rods, stones
in grooves, and so on to actually manipulate numbers. The
Sun
Zi Suan Jing, dating from fifth century China, provides
instructions (algorithms) for multiplication, division, and
square and cube root extraction using bamboo counting sticks
(or written symbols representing them). The result of the
computation was then written using the numerals of the language.
The written language was thus a way to represent numbers, but
not compute with them.
Many of the various forms of numbers and especially computational
tools such as the abacus came ever-so-close to stumbling on the
place value system, but it was in India, probably before the
third century B.C. that a positional
decimal number system including zero as a place holder, with
digit forms recognisably ancestral to those we use today
emerged. This was a breakthrough in two regards. Now, by
memorising tables of addition, subtraction, multiplication,
and division and simple algorithms once learned by schoolchildren
before calculators supplanted that part of their brains, it was
possible to directly compute from written numbers. (Despite
this, the abacus remained in common use.) But, more profoundly,
this was a universal representation of whole numbers.
Earlier number systems (with the possible exception of that
invented by Archimedes in
The Sand Reckoner
[but never used practically]) either had a limit on the largest number
they could represent or required cumbersome and/or lengthy conventions
for large numbers. The Indian number system needed only ten symbols
to represent any non-negative number, and only the single
convention that each digit in a number represented how many of that
power of ten depending on its position.
Knowledge diffused slowly in antiquity, and despite India being on
active trade routes, it was not until the 13th century
A.D. that
Fibonacci
introduced the new number system, which had been transmitted
via Islamic scholars writing in Arabic, to Europe in
his
Liber
Abaci. This book not only introduced the new number
system, it provided instructions for a variety of practical
computations and applications to higher mathematics. As revolutionary
as this book was, in an era of hand-copied manuscripts, its
influence spread very slowly, and it was not until the
16th century that the new numbers became almost universally used.
The author describes this protracted process, about which a great deal
of controversy remains to the present day.
Just as the decimal positional number system was becoming established
in Europe, another revolution in notation began which would
transform mathematics, how it was done, and our understanding of
the meaning of numbers. Algebra, as we now understand it, was known
in antiquity, but it was expressed in a rhetorical way—in words.
For example, proposition 7 of book 2 of Euclid's Elements
states:
If a straight line be cut at random, the square of the whole
is equal to the squares on the segments and twice the
rectangle contained by the segments.
Now, given such a problem, Euclid or any of those following in
his tradition would draw a diagram and proceed to prove from
the axioms of plane geometry the correctness of the statement.
But it isn't obvious how to apply this identity to other
problems, or how it illustrates the behaviour of general
numbers. Today, we'd express the problem and proceed as
follows:
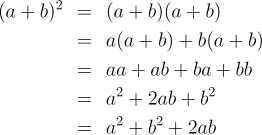
Once again, faced with the word problem, it's difficult to know where to begin,
but once expressed in symbolic form, it can be solved by applying rules of
algebra which many master before reaching high school. Indeed, the process of
simplifying such an equation is so mechanical that computer tools are readily
available to do so.
Or consider the following brain-twister posed in the 7th century
A.D. about the Greek mathematician
and father of algebra
Diophantus:
how many years did he live?
“Here lies Diophantus,” the wonder behold.
Through art algebraic, the stone tells how old;
“God gave him his boyhood one-sixth of his life,
One twelfth more as youth while whiskers grew rife;
And then one-seventh ere marriage begun;
In five years there came a bounding new son.
Alas, the dear child of master and sage
After attaining half the measure of his father's life
chill fate took him.
After consoling his fate by the science of numbers for
four years, he ended his life.”
Oh, go ahead, give it a try before reading on!
Today, we'd read through the problem and write a system of two
simultaneous equations, where x is the age of Diophantus
at his death and y the number of years his son lived.
Then:
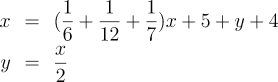
Plug the second equation into the first, do a little algebraic symbol
twiddling, and the answer, 84, pops right out. Note that not only are
the rules for solving this equation the same as for any other, with a
little practice it is easy to read the word problem and write down the
equations ready to solve. Go back and re-read the original problem and
the equations and you'll see how straightforwardly they follow.
Once you have transformed a mass of words into symbols, they invite you
to discover new ways in which they apply. What is the solution of the
equation x+4=0? In antiquity many would have said the
equation is meaningless: there is no number you can add to four to
get zero. But that's because their conception of number was too
limited: negative numbers such as −4 are completely valid and
obey all the laws of algebra. By admitting them, we discovered
we'd overlooked half of the real numbers. What about the solution
to the equation x² + 4 = 0? This was again considered
ill-formed, or imaginary, since the square of any real number, positive
or negative, is positive. Another leap of imagination, admitting the
square root of minus one to the family of numbers, expanded the
number line into the
complex plane,
yielding the answer 2i as
we'd now express it, and extending our concept of number into one which
is now fundamental not only in abstract mathematics but also science and
engineering. And in recognising negative and complex numbers, we'd
come closer to unifying algebra and geometry by bringing rotation
into the family of numbers.
This book explores the groping over centuries toward a symbolic
representation of mathematics which hid the specifics while revealing
the commonality underlying them. As one who learned mathematics
during the height of the “new math” craze, I can't recall
a time when I didn't think of mathematics as a game of symbolic
transformation of expressions which may or may not have any
connection with the real world. But what one discovers in reading
this book is that while this is a concept very easy to brainwash
into a 7th grader, it was extraordinarily difficult for even some
of the most brilliant humans ever to have lived to grasp in the
first place. When Newton invented calculus, for example, he always
expressed his “fluxions” as derivatives of time, and
did not write of the general derivative of a function of arbitrary variables.
Also, notation is important. Writing something in a more expressive
and easily manipulated way can reveal new insights about it. We benefit
not just from the discoveries of those in the past, but from those who
created the symbolic language in which we now express them.
This book is a treasure chest of information about how the language of
science came to be. We encounter a host of characters along the way,
not just great mathematicians and scientists, but scoundrels, master
forgers, chauvinists, those who preserved precious manuscripts and those
who burned them, all leading to the symbolic language
in which we so effortlessly write and do mathematics today.

- Osborn, Stephanie.
The Case of the Displaced Detective Omnibus.
Kingsport, TN: Twilight Times Books, 2013.
ASIN B00FOR5LJ4.
-
This book, available only for the Kindle, collects the first four novels
of the author's Displaced Detective series. The individual
books included here are
The Arrival,
At Speed,
The Rendlesham Incident, and
Endings and Beginnings.
Each pair of books, in turn, comprises a single story, the first
two The Case of the Displaced Detective and the
latter two The Case of the Cosmological Killer. If you
read only the first of either pair, it will be obvious that the
story has been left in the middle with little resolved. In the trade
paperback edition, the four books total more than 1100 pages, so
this omnibus edition will keep you busy for a while.
Dr. Skye Chadwick is a hyperspatial physicist and chief scientist of
Project Tesseract. Research into the multiverse and brane world
solutions of string theory has revealed that our continuum—all of
the spacetime we inhabit—is just one of an unknown number adjacent
to one another in a higher dimensional membrane (“brane”), and
that while every continuum is different, those close to one another in
the hyperdimensional space tend to be similar. Project Tesseract,
a highly classified military project operating from an underground laboratory
in Colorado, is developing hardware based on advanced particle physics
which allows passively observing or even interacting with these other
continua (or parallel universes).
The researchers are amazed to discover that in some continua characters
which are fictional in our world actually exist, much as they were
described in literature. Perhaps Heinlein and Borges were right in
speculating that fiction exists in parallel universes, and maybe
that's where some of authors' ideas come from. In any case, exploration
of Continuum 114 has revealed it to be one of those in which Sherlock
Holmes is a living, breathing man. Chadwick and her team decide to
investigate one of the pivotal and enigmatic episodes in the Holmes
literature, the fight at Reichenbach Falls. As Holmes and Moriarty
battle, it is apparent that both will fall to their death. Chadwick
acts impulsively and pulls Holmes from the brink of the cliff, back
through the Tesseract, into our continuum. In an instant, Sherlock Holmes,
consulting detective of 1891 London, finds himself in twenty-first
century Colorado, where he previously existed only in the stories of
Arthur Conan Doyle.
Holmes finds much to adapt to in this often bewildering world, but then
he was always a shrewd observer and master of disguise, so few people
would be as well equipped. At the same time, the Tesseract project
faces a crisis, as a disaster and subsequent investigation reveals
the possibility of sabotage and an espionage ring operating within
the project. A trusted, outside investigator with no ties to the
project is needed, and who better than Holmes, who owes his life to it?
With Chadwick at his side, they dig into the mystery surrounding the
project.
As they work together, they find themselves increasingly attracted
to one another, and Holmes must confront his fear that emotional
involvement will impair the logical functioning of his mind upon
which his career is founded. Chadwick, learning to become
a talented investigator in her own right, fears that a deeper than
professional involvement with Holmes will harm her own emerging
talents.
I found that this long story started out just fine, and indeed I recommended
it to several people after finishing the first of the four novels
collected here. To me, it began to run off the rails in the second
book and didn't get any better in the remaining two (which begin with
Holmes and Chadwick an established detective team, summoned to help with
a perplexing mystery in Britain which may have consequences for all
of the myriad contunua in the multiverse). The fundamental problem is
that these books are trying to do too much all at the same time. They
can't decide whether they're science fiction, mystery, detective procedural,
or romance, and as they jump back and forth among the genres, so little
happens in the ones being neglected at the moment that the parallel
story lines develop at a glacial pace. My estimation is that an
editor with a sharp red pencil could cut this material by 50–60%
and end up with a better book, omitting nothing central to the story and
transforming what often seemed a tedious slog into a page-turner.
Sherlock Holmes is truly one of the great timeless characters in literature.
He can be dropped into any epoch, any location, and, in this case, anywhere
in the multiverse, and rapidly start to get to the bottom of the situation
while entertaining the reader looking over his shoulder. There is nothing
wrong with the premise of these books and there are interesting ideas and
characters in them, but the execution just isn't up to the potential of the concept.
The science fiction part sometimes sinks to the techno-babble level of
Star Trek (“Higgs boson injection beginning…”).
I am no prude, but I found the repeated and explicit sex scenes a bit
much (tedious, actually), and they make the books unsuitable for younger
readers for whom the original Sherlock Holmes stories are a pure delight.
If you're interested in the idea, I'd suggest buying just the first book
separately and see how you like it before deciding to proceed, bearing in mind
that I found it the best of the four.