Programming Cards
Programs for The Analytical Engine were to be punched on pasteboard Jacquard cards. Babbage envisioned three different kinds of cards, each with its own independent reader:
To a modern reader familiar with contemporary computer architectures, this rigid separation between instructions, immediate constants, and storage references seems curious. Babbage envisioned these kinds of cards as separate for excellent reasons stemming from the mechanics of the Engine. Each kind of card has a very different format: for an Operation card, four holes probably suffice to encode the arithmetical operations. A Number card, by comparison, requires one column of 10 holes for each of the 50 digits of the number it contains, plus a column to indicate the sign. A Variable card falls in between these extremes; it must specify the location in the Store (column 0 to 999 in Babbage's design), and the source or destination axis in the Mill, and whether, on a transfer to the Mill, the column in the Store is to be zeroed.
With separate machinery required for every column of every card, tremendous simplification was achieved by providing a separate, purpose-built, reader for each kind of card, even though some additional components would be required to co-ordinate the motion of the separate streams of cards. In our emulation of The Analytical Engine, we have chosen to abstract the separate streams of cards into a single stream which represents the order in which the cards from the several streams in Babbage's design would have been presented to the Engine. We believe this departure is justified by the following reasons:
We also allow some additional flexibility in the format of the various cards, not requiring numbers to be right-justified to 50 columns or contain leading zeroes, as would certainly have been the case with a mechanical Engine. Again, our goal is to remove unnecessary obstacles to understanding the Engine without compromising the accuracy of the emulation of its capabilities.
A program for The Analytical Engine is composed of a chain of cards of different varieties and content. In our emulation of the Engine, the chain is represented by a series of lines in a text file, one card per line. To run a calculation on the Engine, the card chain prepared by the analyst is submitted to the Engine's human attendant, who examines it for possible errors and requests for actions by the Attendant (for example, to include the cards for a previously-prepared standard computation such as the extraction of the square root of a number at a certain point in the submitted chain).
After completing all requests for attendant assistance in preparing the chain and determining that it is free of obvious errors, the attendant mounts the chain on the Card Reader and causes the Engine to begin to process it. The operation of the Engine may be halted by reaching the end of the chain, by a card which directs the Engine to stop, or by a card which pauses the processing of the Engine and requests (by a visible annotation written on the card) the attendant to take some action and then resume the operation of the Engine.
Number cards are the means by which constants are introduced into the calculation. Each number card contains the letter “N” as the first character, followed by the number of the column in the Store (0 to 999) into which the constant is to be placed, followed by the 50-digit value of the constant. For example, the following zeroes column 1 in the store, places the number 10,000 in column 275, and sets column 302 to −1321.
N001 +00000000000000000000000000000000000000000000000000 N275 +00000000000000000000000000000000000000000000010000 N302 −00000000000000000000000000000000000000000000001321
A mechanical realisation of The Analytical Engine would certainly have required punching numbers into fixed columns with leading zeroes and explicit signs as above. To simplify preparing and reading programs, our emulation allows you to dispense with leading zeroes and place the store column number and value in any columns, and to omit signs for positive values. The above example can thus be simplified to:
N1 0 N275 10000 N302 −1321
The omitted leading zeroes and alignment in columns can be thought of as being done in the process of preparing the cards for a given calculation.
The various operation cards select the arithmetic operation the Mill is to perform on arguments subsequently transferred to it. The operation cards therefore represent the four arithmetic operations, each consisting of the sign for that operation as the first character of the card; the rest of the card is ignored. The four kinds of operation cards are thus:
+ Add − Subtract × or * Multiply ÷ or / Divide
Once the Mill has been set to perform a given arithmetical operation, it will continue to do that operation on each pair of arguments transferred it; another operation card is required only to select a different operation.
In the discussion of the various operations of the Mill, it is necessary to recall that the Mill has two 50 digit Ingress Axes to which arguments are transferred, with the first Ingress Axis having an auxiliary 50 digit Primed Axis which receives the most significant 50 digits when a 100 digit number is divided by a number of up to 50 digits. Results from an arithmetic operation appear on the Mill's 50 digit Egress Axis, which is also accompanied by a 50 digit Primed axis which, in the case of division, receives the quotient while the remainder appears on the main Egress Axis. In addition, the Mill has a Run-up Lever which is activated when exceptional conditions arise during an arithmetic operation.
The variable cards direct the transfer of columns in the Store to the Mill to participate in an arithmetic operation, and the transfer of results from the Mill back to the Store. Each variable card has a letter as its first character which identifies its function:
- L
- Transfer from Store to Mill Ingress Axis, leaving Store column intact.
- Z
- Transfer from Store to Mill Ingress Axis, zeroing Store column.
- S
- Transfer from Mill Egress Axis to Store column.
This function letter is followed by the column in the Store (000 to 999) to or from which the transfer is to be made. If a prime mark appears after the column number, the transfer is made to the Primed Ingress (“L” or “Z” card) or from the Primed Egress (“S” card) Axis of the Mill. Transferring in the first argument to the Mill zeroes the Primed Ingress Axis, so there is no need to transfer to it unless a nonzero value is required. Transferring the second (non-Primed) argument causes the Mill to perform the arithmetic operation and place the results on the Egress (and for multiplication and division, Primed Egress) Axis, from which they may be transferred back to the Store.
The following sequence of Number, Operation, and Variable cards places the number 10,000 in column 1 of the store and 28 in column 2, sets the Mill to perform division, transfers in the dividend, 10,000, and the divisor, 28, and then transfers the quotient from the Primed Egress Axis to column 3 in the Store and remainder from the Egress Axis to column 4.
This example, and many of those which follow, can be run in the Web emulator by clicking the gears icon at the right of the page. Every example which bears this icon can be run by clicking it.
N001 +00000000000000000000000000000000000000000000010000
N002 +00000000000000000000000000000000000000000000000028
÷
L001
L002
S003'
S004
When the Engine completes processing these cards, column 3 in the store will contain the quotient, 357, and column 4 the remainder, 4.
As with the Number Cards, our emulation of The Analytical Engine permits you to dispense with the leading zeroes which would have been required by the machinery. The example above can thus be rewritten as the more readable, if less authentic:
N1 10000 N2 28 ÷ L1 L2 S3' S4
When performing calculations with numbers including decimal fractions (fixed point arithmetic in modern terminology), the dividend must be multiplied by 10 to the power of the number of decimal places used in the calculation before the division is performed, and the product of a multiplication must be divided by the same scale factor to adjust the decimal point to the desired location. Performing this decimal place adjustment by multiplication or division would be extremely time-consuming, so Babbage added the capability of shifting numbers in the Mill by a given number of decimal places (with zeroes filling vacated digit positions). This operation, referred to as “stepping up or down” (shifting left or right in contemporary computers), achieves the decimal place adjustment without the need for a lengthy general-purpose multiplication or division. Furthermore, the mechanism by which the Mill performs multiplication and division requires the stepping up and down capability, so employing it for scaling in multiplication and division requires no additional machinery.
All of the documents describing Babbage's designs envisioned stepping up of dividends and stepping down of products as part of the division and multiplication operations, but never described precisely how this was to be specified by the cards controlling the Engine. Our emulation provides stepping up and down with special cards, included in the card stream as a multiplication or division is performed. The stepping up and down cards are:
- <n
- Step up (shift left) by n digits the 100 digit value formed by the most significant 50 digits in the Primed Ingress Axis and the least significant digits in the first Ingress Axis. Digits stepped off the 100th place are lost, and zeroes fill digits vacated by the stepping. The stepped result remains on the Primed Ingress and first Ingress Axes.
- >n
- Step down (shift right) by n digits the 100 digit value formed by the most significant 50 digits in the Primed Egress Axis and the least significant digits in the Egress Axis. Digits stepped off are lost, and zeroes fill digits vacated by the stepping. The stepped result remains on the Primed Egress and Egress Axes.
This seems pretty intimidating at first glance, but a concrete example should clarify how stepping up and down are used in practice. Suppose we want to compute
accurate to six decimal places. First of all, we will provide number cards which place the numbers involved in the calculation into columns in the store, each written with six decimal places. I will omit leading zeroes and take advantage of the emulator's ignoring spaces on number cards to improve readability.
N0 4000000000 N1 2500000 N2 28000000
The Mill knows nothing about decimal places, so just as when computing with tables of logarithms or a slide rule, the analyst keeps track of decimal places. Here, we've placed numbers in the store which are the arguments in the calculation, each multiplied by 1,000,000, with the rightmost six digits representing the decimal places. Next we'll add cards to perform the multiplication:
× L0 L1
Loading the second argument into the Mill causes the multiplication to be performed, after which the Primed Egress and Egress axes contain the 100 digit product, 10000000000000000. This product is 1,000,000 times larger than the desired result, since both arguments to the multiplication were themselves scaled by that factor. To get the correct result, we need to divide the product by the scale factor of 1,000,000 or, achieve the same result much more rapidly by simply shifting the decimal digits of the product six places to the right by stepping down, yielding the true product, 10000000000, which represents 10000.000000. So, before the product is transferred to the Store, a stepping down card is introduced to shift the product six places to the right:
>6 S3
After these cards have been processed, column 4 in the Store will contain the desired product of 10000000000. Now we must turn to the division. Since we're dividing by a number which incorporates the decimal place scale factor of 1,000,000, we must multiply the dividend by the same factor prior to the division so the decimal place in the quotient will appear in the proper place. Again, this scaling can be achieved simply by stepping up, or shifting, the digits of the dividend to the left by six places, setting the new least significant digits to zero. Unlike the case for multiplication, this stepping up is done immediately after transferring the dividend into the first Ingress Axis (and the Primed Ingress Axis, if the dividend exceeds 50 digits), and prior to transferring the divisor to the second Ingress Axis, which causes the Mill to perform the division. Our computation is completed, then, with the cards:
÷ L3 <6 L2 S4'
After which (recall that the quotient appears in the Primed Egress Axis after a division) column 4 in the Store will contain 357142857, to which we may add a decimal point in the chosen position, yielding the result of the division, 357.142857, correct to six decimal places.
Note: the computation above does indeed yield a product correct to six decimal places, but only because the seventh decimal place is less than 5, requiring no rounding of the prior places. To compute a more accurate 6 digit result, we should compute additional places and round to 6 digits. The following cards compute 7 digits of quotient and round to 6.
N0 40000000000 N1 25000000 N2 280000000 N3 5 N4 10 × L0 L1 >7 S5 ÷
None of the calculations presented so far have involved decisions in which the arithmetic operations performed depend on the values of one or more of the variables involved. Suppose, for example, that as part of a computation of tables of probability and statistics we have calculated a number, placed it in the Store, and now for the next step in the evaluation we need the factorial of the number just computed. The factorial of any positive integer n is defined as:
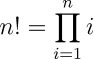
Now, the only operations required for the computation of the factorial are multiplication and subtraction which, as we've seen already, are done easily enough with the Engine. To compute the factorial of 6, for example, we can write out the series on Number, Operation, and Variable cards as follows, in which Store column 0 holds the iteration variable, column 1 supplies the constant 1 used to decrement it on each step, and the product is accumulated in column 2. After the Engine has processed these cards, column 2 will contain 720, the correct value for 6!.
N0 6 N1 1 N2 1 × L2 L0 S2 − L0 L1 S0 × L2 L0 S2 −
This works fine when we know the value for which the factorial is to be calculated (albeit being tedious to prepare, read, and wasteful of pasteboard cards), but what do we do when we don't know the value whose factorial is to be taken at the time the cards are prepared? Suppose, for example, a previous calculation has placed a number n in column 0 of the Store, and we wish to place its factorial in column 1. The computation of the factorial for any number whatsoever inherently requires the Engine to make a decision, and the Combinatorial Cards which allow it do just that.
The Engine's Card Reader is not constrained to simply process the cards in a chain one after another from start to finish. It can, in addition, directed by the very cards it reads and advised by the whether the Mill's run-up lever is activated, either advance the card chain forward, skipping the intervening cards, or backward, causing previously-read cards to be processed once again. This can be accomplished with the following, general and more compact sequence of cards, taking the factorial of 6 as above, but usable with any number supplied in column 0 whose factorial is fewer than 50 digits in length.
N0 6 N1 1 N2 1 × L1 L0 S1 −
The last card in this sequence is where the magic occurs; it's our first encounter with a combinatorial card. Let's dissect it in detail. The first character “C” identifies it as a combinatorial card. The second character is either:
- F
- Advance (skip forward) cards in the reader.
- B
- Back (skip backward and repeat) cards in the reader.
The third character indicates whether the advancing or backing is always performed (unconditional), or whether it depends on Mill's run-up lever.
- +
- Always advance (“F”) or back (“B”) cards.
- ?
- Advance (“F”) or back (“B”) cards only if the Mill's run-up lever is set.
The number starting in column 4 indicates how many cards are to be advanced past or backed up past the reader. To understand this number, it's important to keep in mind that at the time the card chain is advanced or backed up, the combinatorial card itself has already been read, and the Card Reader advanced to the next card in the chain. Therefore, the starting point for counting how many cards to back or advance is the card after the combinatorial card, not the card itself.
Now we know enough to dissect the example above. We start by loading the number for which we wish the factorial in column 0 of the store, the constant 1 in column 2, and we initialise column 1, in which we will accumulate the factorial, to 1. The multiplication and the three Variable Cards which follow multiply the current value in column 0 by the product so far in column 1, placing the product back in column 1. Next, the constant 1 is subtracted from the value in column 0, placing the decremented value back in column 0, ready to be used in the next cycle. Now we wish to determine whether the end of the calculation has been reached. Since the Mill has already been set to perform subtraction, there is no need for a new Operation card. The next two variable cards load the constant 1 and subtract from it the present value in column 0. As long as the value in column 0 is greater than one, this subtraction will cause the run-up lever in the Mill to be set since the difference has a different sign than the first argument, but once column 0 has been counted down to one, the subtraction, 1 − 1, will not set the run-up lever. We aren't interested in the numerical result from this subtraction on the Mill's Egress Axis, only whether performing it set the run-up lever, so we don't bother to transfer the result back to the store. Next the Engine reads the combinatorial card. The appearance of the “?” character in the third column makes the backing of the card chain indicated by the “B” in the second column conditional on the setting of the run-up lever, and the count of 11 backs up to the start of the multiplication step (recalling that the count must include the combinatorial card itself).
Thus, the effect of the combinatorial card is to cause the multiplication and subtraction steps which precede it to be repeated as long as the value in column 1, which starts out as the number whose factorial we wish, is greater than one. This can be seen then, to yield the factorial of any number we start out with in column 0 (as long as its factorial does not exceed the 50 digit capacity of the Mill and Store).
Conditional and unconditional advancing of the card chain allows decisions to be made based on calculated values. Suppose we have calculated a value and placed it on column 0 of the store and that we now need the absolute value of that quantity. Since the value in column 0 has arisen from earlier computation, we do not know its sign at the time the cards are prepared, so the Engine must decide whether to negate the value based on its sign. The following sequence of cards replaces the number in column 0 of the Store with its absolute value:
N1 0 + L1 L0 CF?1 CF+4 − L1 L0 S0
We start by loading the constant 0 into column 1 of the Store, then add zero to the unknown quantity in column 0. Addition sets the run-up lever if the sum of two quantities differs in sign from the first argument; since we are adding the unknown to zero, the run-up lever will be set only when the number in column 0 is negative. As in the factorial example previously, we are interested only in whether the addition set the run-up lever, not the sum, so we do not bother to transfer the sum to the Store.
The conditional combinatorial card “CF?1” causes the card following it, the unconditional combinatorial card “CF+4” to be skipped if the run-up lever is set. Skipping this card causes the quantity in column 0 to be subtracted from zero, inverting its sign, and returning the absolute value to column 0. If the run-up lever is not set, the “CF+4” will not be skipped and, when processed, will advance the card chain past the subtraction, leaving the positive value in column 0 intact. Thus, this sequence of cards inverts the sign of the number in column 0 only if it is negative to begin with, thereby obtaining the absolute value.
A variety of Action Cards perform non-arithmetic operations related to the calculation. The Action Cards are:
- B
- Ring a bell to attract the attention of the attendant.
- H
- Halt the Engine. The Engine ceases reading cards, leaving the Halt card visible in the Card Reader so the attendant may observe any annotation written on it.
- P
- Print the result of the last arithmetic operation performed by the Mill on the Printing Apparatus.
The following example, which might be used at the start of a set of cards used to extract the square root of a number in column 0 of the Store, illustrates how Action Cards are used. If due to an error on the part of the analyst in formulating a calculation for the Engine, or resulting from faulty preparation of the cards, an attempt is made to extract the square root of a negative quantity, it is better to halt the calculation at that point and alert the attendant of the problem than to continue a calculation whose result will inevitably prove erroneous. The cards below use the same technique we employed previously to compute the absolute value but here, if we find the value in column 0 to be negative we print the offending number on the printer, ring the bell to alert the attendant, and halt the Engine. Upon examining the Card Reader, the annotation handwritten on the card which halted the Engine informs the attendant of the nature of the problem. If the argument to the square root extraction is non-negative, the error reporting sequence is skipped and calculation continues.
N1 0 + L1 L0 CF?1 CF+3 P B H Cannot take square root of negative number
Any card with a period (“.”) or blank character in column 1 causes no action by the Engine; the Card Reader simply advances to the next card. Why include cards which don't do anything except consume time? These Comment Cards allow inclusion of textual notes meaningful to the analyst and/or the Engine's attendant, but ignored by the Engine itself. Such notes can be very useful in explaining how the various cards accomplish a calculation, especially when examining a calculation prepared by another analyst. Later, should calculation speed prove an overriding concern, the comments can always be removed from the card chain.
Even though comment cards cause no action by the Engine, they do appear in the card chain, and combinatorial cards must include them in the number of cards the Card Reader is to advance or back up.
The following example uses Number, Operation, Variable, Action, and Comment cards to in a calculation which extracts the square root of a number with 20 decimal places, checking for negative arguments, and including an optional step which prints intermediate values of the root prior to convergence.
Extract square root by Newton's method x² = N x[k+1] = (N ÷ x[k] + x[k]) ÷ 2 V0 N (Input), x (Output) V1 0.5 V2 x[k] V3 scratch V4 0 V5 x[k−1] V6 largest positive number Since multiplication is much faster than division, we substitute a multiplication by fixed point 0.5 for the division by 2. Input, calculations, and output are in fixed point with 20 decimal places. Load V0 with the number whose root we wish to extract: N000 200000000000000000000 12345678901234567890 N001 50000000000000000000 N004 0 N006 9999999999999999999999999999999999999999 Make sure argument is non-negative + L004 L000 CF?1 CF+3 P B H Cannot take square root of negative number (on printer) Calculate initial guess as N ÷ 2 ÷ L000 <20 L001 S002' Cycle here to perform iterations of Newton's method until the result converges to the square root. Save current term for convergence test + L002 L004 S005 Compute N ÷ x[k] ÷
The “P” action card which follows the line flagged with asterisks in the right margin is an example of how comments can facilitate the testing of a program. Since any card with a blank first column is ignored, we can include cards intended for testing a calculation, in this case printing intermediate values prior to convergence, then remove the diagnostic output simply by indenting those cards. Should a subsequent error require further testing, the diagnostic output can be easily restored. Of course, it's a lot easier to indent text on a modern computer than holes on a pasteboard card, but Analytical Engine programmers would undoubtedly have simply flipped the diagnostic cards over, placing the unpunched rightmost columns under the reader, transforming them into comment cards until needed again. FORTRAN programmers in the IBM card mainframe era used a similar trick: they would punch a “C” in column 80 of diagnostic cards so that when flipped over they would be treated as comments and ignored. Since flipped cards were easily located in a deck thanks the the corner cut, it was easy to flip them back if needed.
The Curve Drawing Apparatus allows graphical plots to be made of quantities calculated by the Engine. As Babbage remarked in his 1837 description of the Engine, “The discovery of laws from the examination of a multitude of tabulated and reduced observations is greatly assisted by the representation of such tables in the form of curves.”
In the absence of an explicit description of how the Curve Drawing Apparatus was envisioned to operate, our emulator assumes that a specific fixed decimal point would have been chosen for use with the Apparatus, with the decimal point in the middle of the 50 digit capacity of the Mill and Store, and that values would be transferred for curve drawing in the same manner they are printed: from the most recently accessed axis of the Mill. We further assume that the Apparatus draws curves within a fixed domain and range of ±1.0, with the scaling of co-ordinates to be drawn into that range the responsibility of the analyst.
The Curve Drawing Apparatus is controlled by the following cards.
- DX
- Transfer result of last arithmetic operation by the Mill to Curve Drawing Apparatus X co-ordinate.
- DY
- Transfer result of last arithmetic operation by the Mill to Curve Drawing Apparatus Y co-ordinate.
- D−
- Raise pen. The next “D+” card will begin a new segment of the curve.
- D+
- Lower pen and draw to current X and Y co-ordinates.
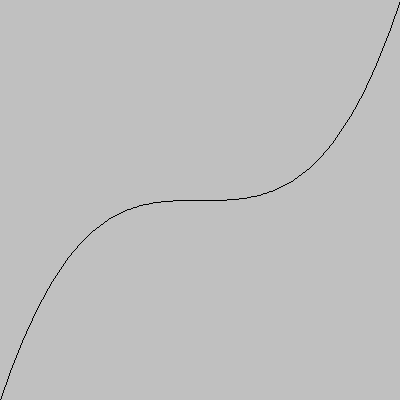
The following sequence of cards plots the function:
for the domain −1 ≤ x ≤ 1.
Iteration variable N000 −10000000000000000000000000 Step N001 100000000000000000000000 Number of steps N002 201 Constants N003 1 N004 0 + L000 DX × L000 L000 >25 S005
Yielding the plot:
| Curve Drawing Apparatus |
|---|
|
The Analytical Engine was always envisioned to have a human attendant who prepared calculations for the Engine, supervised its operation, intervening when errors or circumstances requiring human attention occurred, and maintained the library of standard calculations and tables employed by users of the Engine. Since many hours of the attendant's time would be spent simply watching the Engine run, we envision that the attendant would use this time to assist analysts in preparing computations for the machine, particularly with clerical tasks performed better by an individual intimately familiar with the details of the Engine than by an analyst whose expertise centres on the mathematical aspects of the calculation.
Attendant Request Cards are cards, inserted among those processed directly by the Engine, which the attendant examines and replaces with cards which the Engine processes directly, or which instruct the attendant to format or annotate the results of the computation in various ways.
- T1
- Begin calculation trace.
- T0
- End calculation trace.
When a calculation produces an incorrect result, the cause is usually an error on the part of the analyst, not an insect trapped in the machinery. A calculation trace can often isolate the error, allowing it to be corrected. The attendant replaces the T1 card with an “H” card which halts the engine and indicates a trace is requested at this point. From that point, until a T0 card is encountered, the attendant manually cranks the engine, writing down every card read, every transfer between the Mill and the store, and the result of each calculation performed by the Mill. Suppose, for example, the analyst submits the following calculation:
N0 10000 N1 5 ÷ L000 L001 S002' P
and doesn't understand why the 0 appears on the printer instead of 2000, the quotient when 10000 is divided by 5. Resubmitting the calculation with a trace request:
T1 N0 10000 N1 5
causes the attendant to provide the analyst with the following handwritten log of the Engine's operation.
Card: 2. (badcalc.ae:2) N0 10000
Store: V0 = 10000
Card: 3. (badcalc.ae:3) N1 5
Store: V1 = 5
Card: 4. (badcalc.ae:4)
Card: 5. (badcalc.ae:5) ÷
Card: 6. (badcalc.ae:6) L000
Store: Mill <= V0(10000)
Card: 7. (badcalc.ae:7) L001
Store: Mill <= V1(5)
Mill: 10000 / 5 = 2000, Rem: 0
Card: 8. (badcalc.ae:8) S002
Store: V2 = 0
Card: 9. (badcalc.ae:9)
Card: 10. (badcalc.ae:10) P
0
Reading this log, the analyst slaps his forehead upon realising that at card 8, he erroneously stored the remainder, placed by a division on the Egress Axis, rather than the quotient from the Primed Egress Axis. Replacing card 8 with:
S002'
corrects the error and causes the Engine to print the quotient, 2000. Often an error is known to occur in a small portion of a much longer calculation. Placing a T1 card at the start of the suspect sequence and a T0 at the end causes the attendant to trace only the intervening cards. This reduces the length of the log the analyst must peruse, and keeps the attendant from becoming cranky.
- (
- Unconditional cycle (backing) start.
- (?
- Conditional cycle (backing) start.
- )
- End cycle (backing).
- {
- Unconditional skip (advancing) start.
- {?
- Conditional skip (advancing) start.
- }{
- Conditional skip alternation (else clause).
- }
- End skip (advancing).
One of the most common sources of error is advancing or backing an incorrect number of cards as a result of a combinatorial card. When a new calculation is being prepared, every change which adds or removes cards within the range of a combinatorial card must be accompanied by a change in the count on the card. The cycle cards, which contain a left (start of cycle) or right (end of cycle) parenthesis as the first character, specify backing of the card chain. If a question mark appears as the second character of the card marking the beginning of the cycle, the backing is conditional on the run up lever being set at the end of the cycle. The attendant replaces the cards denoting the cycle with a combinatorial card at the end of the cycle with the proper number of cards to back. Here is a simple card chain which prints the squares of the numbers from 1 to 10, in which the analyst has expressed the cycle with conditional backing cards, flagged in blue.
N000 1 N001 1 N002 11 (? ×
The attendant counts the number of cards in the cycle, and prepares the following card chain for the Engine. The combinatorial card added by the attendant is highlighted in red.
N000 1
N001 1
N002 11
×
L000
L000
P
+
L000
L001
S000
−
L000
L002
CB?12
H
While backing the card chain is generally used to repeat sequences in a calculation, advancing permits decisions to be made based on the results of a calculation. Advancing block cards are replaced by the attendant with corresponding combinatorial advancing cards, with the attendant counting the number of intervening cards and supplying the correct advancing count. Suppose that in the course of a calculation we have placed a value in column 1 of the Store and that we need its absolute value in the next step; in other words, if it is negative, we need to invert the sign to obtain the absolute value. A sequence of cards which replaces the value in column 1 of the Store with its absolute value is as follows, with column 1 being loaded explicitly with −10 for this test case. The advancing cards are shown in blue, and cards to print the result appear after the computation of the absolute value.
N001 −10 N000 99999999999999999999999999999999999999999999999999 N002 0 + L000 L001 {?
The attendant translates the advancing cards into a combinatorial card and mounts the following chain on the card reader.
N001 −10
N000 99999999999999999999999999999999999999999999999999
N002 0
+
L000
L001
CF?4
−
L002
L001
S001
+
L001
P
This sequence works by adding the number in column 1 to the largest positive value, placed in column 0, which will cause a run up if the value in column 1 is greater than zero, causing a subtraction of the column 1 value from zero, which inverts its sign, to be skipped in that case.
Conditional and unconditional advancing cards, used together, permit the Engine to evaluate expressions which depend upon an intermediate value in the calculation. For example, consider the following step in the evaluation of a function:
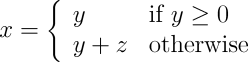
The alternation card, “}{”, permits this computation to be encoded straightforwardly as follows. The comment cards at the top give the assignment of variables to columns in the store.
Store Variable 000 x 001 y 002 z N001 −100 N002 1000 N003 0 + L003 L001 {?
We add the variable y to zero, which will cause a run up and skip to the second part of the alternation only if y is less than zero. Then in the first part of the alternation, we can simply store y into column 0, representing x. The second part of the alternation adds y and z (recall that since the Mill has already been set to perform addition, no operation card need be supplied) and stores the sum into x. The attendant translates the advancing cards into combinatorial cards as follows:
N001 −1 N002 1000 N003 0 + L003 L001 CF?2 S000 CF+3 L001 L002 S000 L000 P
The first conditional advancing card skips to the case for negative x, while the second unconditional advancing card skips past the cards for the negative case after storing the greater than or equal to zero value of y into x.
The Engine was envisioned to be accompanied by a library of sequences of cards for commonly used calculations, for example extracting square roots or evaluating trigonometric functions. An analyst, when preparing a calculation involving these functions, would simply request the attendant to incorporate the cards for each function required at the proper point in the submitted calculation. The following two attendant request cards provide access to the library of our emulation of the Engine.
- A include cards filename
- Include cards from local file filename.
- A include from library cards for libname
- Include cards from Engine's standard library for calculation libname.
The “A include cards” form interpolates cards from a file on the computer which is running the emulator; the filename must conform to the conventions of that computer's operating system. If the environment in which the emulator is running does not allow access to local files (this is often the case when the emulator is run within a Web browser), this form of library request cannot be used.
The “A include from library cards for” request obtains cards for the calculation libname from a standard library location specified in the configuration of the emulator. When running the emulator stand-alone on your computer, this will usually be the name of a directory in which you keep your library of standard calculations. Web browser implementations of the emulator usually provide the library on the Web site hosting the emulator. Consult the library documentation published by the host site for a list of library calculations available there and instructions for using them.
A frequent source of error when calculating with decimal numbers (fixed point arithmetic) is miscounting decimal digits in constants, or specifying incorrect stepping up and down counts to adjust decimal places. The decimal place expansion cards delegate these clerical tasks to the attendant, who can be entrusted, as always, to faithfully and flawlessly carry out the requests of the esteemed analyst. The attendant is informed of one's wish to calculate with a given number of decimal places with the card:
- A set decimal places to n
- Expand decimal points on number cards and unspecified stepping up and down counts for calculations with n decimal places.
Subsequent number cards which contain numbers including a decimal point, “.”, are expanded to integers with the desired number of decimal places, adding zeroes and/or discarding excess decimal places and rounding as required. The following sequence of cards illustrates decimal place expansion:
A set decimal places to 10 N000 12 N001 12.0 N002 3.1415926535897932384626434 N003 7.0
The attendant prepares the following cards for the Engine:
N000 12 N001 120000000000 N002 31415926536 N003 70000000000 ÷ L001 <10 L003 S004' P
Note that the number card loading “12” into column 0 was not modified; only numbers which include a decimal point are rewritten by the attendant. The value for π given on the card for column 2 contained more than the requested 10 digits, so the attendant rounded it to 10 digits. The stepping up card in the division contained no count, so the attendant filled in the requested number of decimal places. Stepping up and down cards which contain a number are not modified.
Advanced analysts should note that the attendant's willingness to expand decimal places and fill in stepping counts allows the preparation of library calculations which work for any number of decimal places within the capability of the Engine. If library calculations are written with all constants given in decimal form and all stepping up and down counts left for the attendant to fill in, they will work with whatever number of decimal places the analyst requests. If a library calculation needs to use more decimal places than the calculation which includes it, it may specify a number of decimal places relative to the present setting by preceding the count with a plus (more places) or minus (fewer places) sign. The following sequence illustrates relative decimal place requests.
A set decimal places to 5 N000 1.0 A set decimal places to +5 N001 1.0 A set decimal places to −5 N002 1.0
This is expanded by the attendant to:
N000 100000 N001 10000000000 N002 100000
The Engine's Printing Apparatus is a simple mechanical device which prints numbers with one column on the paper corresponding to a digit in the current axis of the Mill. Prior to publication as tables, these printed results must be rewritten taking into account decimal places and conforming to the conventional format for the type of table being prepared. The attendant fills free time performing this transcription of numbers into publication form, as specified by the following two request cards.
- A write numbers as picture
- Transcribe numbers from the printer onto the final report of the calculation using the form in the picture.
- A write numbers with decimal point
- Transcribe numbers from the printer onto the final report as decimal numbers according to a previous “A set decimal places to” request.
The second form is the simplest and suffices for many cases. It simply writes numbers with a decimal place in the position specified by the last “A set decimal places to” request. For example, the cards:
A set decimal places to 10 A write numbers with decimal point N001 12.0 N002 7.0
prints the result as “1.7142857142” rather than “17142857142” as would be printed were the “A write numbers with decimal point” request absent.
If more complex formatting of results is required, the “A write numbers as” card may be used to furnish the attendant an example, or picture, of how numbers should be written in the transcription of the raw results from the Printing Apparatus. All characters of the picture not in the following table are simply transcribed as-is, allowing annotation to be included in the results. The number is edited according to the following formatting characters, processing the picture right to left.
If a number on the Printing Apparatus contains more digits than are specified in the picture, the attendant copies the additional digits at the start of the number. If a printed number is negative and no sign was specified in the picture, the attendant writes a negative sign at the left of the number. To print the result of the calculation of the square root of 2 shown above in a more readable form, replace the “P” card at the end with:
A write numbers as 9.99999 99999 99999 99999 P
which will cause the results to be written as:
1.41421 35623 73095 04880
While transcribing results from the Engine's printer to the written report returned to the analyst, the attendant can also add annotations which aid the analyst in interpreting the results without referring back to the cards used in the calculation. A variety of output annotation cards inform the attendant as to how the results are to be transcribed.
- A write in rows
- Transcribe numbers from the printer onto the final report of the calculation with one number per line (this is the default).
- A write in columns
- Transcribe numbers from the printer onto the final report across the page. Spacing, separators, and line breaks must be added by other Output Annotation Cards.
- A write annotation textual annotation
- Add the given textual annotation to the report of the calculation. Trailing spaces are significant, and can be used to separate items when writing in columns.
- A write new line
- Start a new line in the calculation report. This is generally used when writing in columns to end a line of the table being printed.
The “A write in columns” card affords the analyst the greatest control over the presentation of results. Instead of each item occupying a line of its own, the attendant writes items one after another on a line, commencing a new line only upon encountering an “A write new line” card. To illustrate the extent to which the analyst can prescribe how the results are written, let us conclude with a rather frivolous example from the world of commerce. Suppose, some day in the remote future, when Her Majesty's Empire counts among its dominion not only all the worlds attending our Sun, but also innumerable planets around other suns across the void of space, that the inevitable enrichment of Mankind through the eternal march of Progress should render Analytical Engines so economical that dozens, perhaps hundreds, could be built, and might be used not only for the great questions of astronomy and navigation, but even for the mundane computations of bankers and shopkeepers.
It is from that fantasy of the remote future that our closing example is drawn. A merchant has received an order for 337 items, each of which costs 3 pounds six and tuppence, and having no clerk to calculate the total (every person with a mind for figures having disappeared into the lucrative endeavour of designing, constructing, and attending ever more complex and swifter Analytical Engines), resorts to one of those very Engines to perform the computation. The merchant's former clerk, still just a lad but earning a salary shockingly close to the merchant's annual turnover, prepares the following cards for him as a favour. The erstwhile clerk, now Analytical Engineer, includes along with the customary comments, underlined notes to his former employer as to how the cards are to be used.
Price per unit
Replace the following three number cards with the price
of each unit sold in pounds, shillings, and pence respectively.
N010 3 . £
N011 6 . s
N012 2 . d
Number of units purchased
Replace the following number card with the number of units
your customer ordered.
N013 337
You should not have to change any of the following cards;
they are valid for any unit price and quantity whatsoever.
Constants
N000 20 . shillings per pound
N001 12 . pence per shilling
Convert unit price to pence, result in column 2
×
L010
L000
S002
+
L002
L011
S002
×
L002
L001
S002
+
L002
L012
S002
Multiply unit price in pence by quantity purchased
×
L002
L013
S002
Divide by pence per shilling; remainder is pence
÷
L002
L001
S003
S002'
Divide by shillings per pound; quotient is pounds,
remainder is shillings
L002
L000
S004
S005'
Instruct the attendant as to how the result is to be written
A write in columns
A write annotation Total price for
A write numbers as 9
+
L013
P
A write annotation items is
A write numbers as £#,##9
+
L005
P
A write numbers as 9s
+
L004
P
A write numbers as 9d
+
L003
P
A write new line
When these cards are sent by messenger to the merchant's neighbourhood Analytical Engine, the result comes back within the hour:
Total price for 337 items is £1,114 18s 2d
The merchant writes the total on the bill of lading, almost oblivious to the mechanical achievements of the century in which he lives.